1. Introduction

Generally, electrical power is transmitted from the sending end side to the receiving end substations. At the receiving side, the voltage is stepped down to a lesser value of the sending end value, most times accompanied by some technical and economic challenges. As a result of these challenges, electrical energy being the hub of modern technologies as well as the foundation of industrialization, has driven every nation to improve electrical power generation as well as enhancing the power transmission and distribution systems in order to make it efficient and meet-up with the growing power demand of the respective nations, thus massive upgrading. Despite the perceived upgrade to enhance the power wheeling capacity of the transmission line and its ancillary parts, low voltages are still felt in some areas and this has prompted the installation of distribution generators without adequate arrangement, accordingly causing the over-loading of the different feeders and some other issues. Thus, a few zones are under-used whereas certain transformers are over stacked. In this study, the combined Fast Decoupled – Newton Raphson method was utilized to study the Port Harcourt Zone 4 power network. The Port Harcourt Z4 substation includes 4-distribution transformers using a complete installed capacity/limit of approximately 164.9MVA with nine (9) serving feeders. However, the authority of the substation has attributed blame on poor power situation on insufficient megawatts, adding that there had been a reduction in the megawatts allotted to the substation from 693.9MW to between 149.7MW/159.5MW. This shortage of megawatts forced the company to embark on recurrent load shedding to ensure the limited-megawatts available go round consumers. These are the key problems to be looked upon in the distribution network for proper utilization of the available power. Hence, the objective of this paper is to formulate a load flow program based on the combined Fast Decoupled – Newton- Raphson load flow method.  Analyze, and take care of the issue of successive blackouts brought about by heavy power (I²R) losses in the line, low voltage experienced, poor cos∅ at the load end,  over-loading of feeders, and transformers in the 33kV distribution network.

2. Related Work

Availability of adequate electrical energy supply is an indispensable enabler for the social-economic advance of any nation [1, 2]. Several numeral of resourceful and dependable power flow solution techniques, like, Gauss-Seidel (GS), Newton-Raphson (NR), Fast Decoupled Load Flow (FDLF), and so on were reviewed as in [3, 4]. In an earlier era and now, they were widely and excellently used for network analysis, operation, control, and planning. However, in the investigation of distribution networks with high resistance to reactance proportions (Resistance/Reactance) an exceptional network becomes relevant. Power flow study is an indispensable requirement for power system planning, expansion, and assessment, etc. Many scholars have carried out great research for the improvement of computer programs (CP)  to enhance large power system power flow investigation [5, 6]. Though, these comprehensively useful programs may experience convergence complexities with radial distribution networks when many nodes are to be resolved  [5-7] and, thus, development of a special program (SP) becomes crucial for distribution study. The result formulation and procedure may be accurate or estimated, with balanced values anticipated for either on-line or detached on line use, and intended to be applied for either single-case several-case assessments [3, 8]. The load flow methodology is a key device in application programming for the network distribution management. These approaches can be classified as node-based or branch-based procedure. The node-based class utilizes node voltages and or currents infusion as state variables to address the load flow issue. Here, the most prominent techniques incorporate system equivalence approach strategy, Z-node approach, Fast Decoupled calculation, and Newton-Raphson’s approach. The branch-based procedure uses either branch currents, and or branch flows as main variables for the solution of the load flow issue. Regressive and forward range based procedures, as well as ring impedance calculation algorithms, can be arranged in group ass in [7]. The power losses in electricity are most cases higher at the distribution lines compared to that of the transmission systems. This is usually due to the higher R/X ratio at the distribution lines [2, 6, 9].

2.1. Load Flow Solution methodology for Radial Distribution network

According to [6, 10] power flow procedure is planned for transmission networks rather than distribution systems. Much of the algorithm has been modified in literature. The necessity for dependability, exactness, storage ability, and quick calculation assumes a significant function in any latest power flow proposed distribution analysis. In this study, it was stated that a new distribution power flow methodology must consider complex network so order that the storing capacity can be reduced to achieve the result fast, and in fewer iteration for both online and offline applications [8, 10].

2.2. The Theory of Diakoptic Built On Fast Decoupled Power Flow Algorithm

The hypothesis is reasonable for dispersed processing of load flow problem. The studies can be performed in a very shorter period if calculations for various subsystems of an incorporated network are done simultaneously utilizing a few workstations. However, when distributed processing preparation is carried out continuously in actual time, information should be gathered from nearby points and only a generally little information base is to be updated locally at normal interims. The Reduction of transmission line information over long significant distances to the central workstation can be achieved [8, 10].

2.3. Load Flow Analysis using ETAP Software Simulation

This product is a computer-based model that simulates a continuous real-time stable state power system process. It facilitates the calculation of system line losses, reactive and real power flow, and node voltage profiles [9-11]. ETAP software is used for designing and coordinating of relays in the distribution network [10, 12]. To carry out a power flow study to analyze the performance of the electrical system during abnormal and normal working conditions, and giving the proof expected to upgrade or optimize circuit uses, create functional voltage profiles; identifies transformer tap settings, minimize MVAr, and MV losses. Besides, to help in developing equipment specification guidelines.

2.4. Analysis of the Load Flow Problem in Power System Planning Studies

According to [7, 11, 13], load flow or power flow is the movement of active and reactive power from generators to different load points of the system. This examination is an exceptionally basic instrument utilized by power system engineers for planning and deciding the steady-state activity of a power network. In [10, 12, 14] power system is presented as an electric circuit that comprises of generators, transformers, circuit breakers, lines, etc. to decide the different hub voltages, phase angles, dynamic and responsive power flows through the system [15]. The analysts or researchers in [14, 16, 17] said that the primary proof acquired from the load/power flow consists of voltage and phase angles at a given node number. The load flow problem equations are nonlinear and this requires an iterative technique to solve it.

2.5. Power Perturbation Technique for Study of Power Network Load Flow

Perturbation technique theory is a new power flow technique which goal is to try to improve the convergence rate by linearizing the load flow equation where more attention is given to the voltage values (V) and the phase angle (δ) in every recalculation step. This procedure is quicker, and it gives more precise results than the regular or normal Gauss-Seidal power flow computation method, having been tested on the IEEE 118-node, 30-node, 14-node, and 5-node systems [2, 18, 19]. Reduction of the computational challenges by decreasing the total equations, approximating the Jacobian matrix structure, and other different factors are the opinions of most developed existing algorithms.

3. Methodology of the Research

Among various power flow solution algorithms, power flow models depend more on the Newton-Raphson (NR) based algorithm. Various decoupled polar alternatives of the NR methodology have been tried for minimizing the storage capacity limit and calculation period associated with the load flow remedy. In this study, the tools needed for the study are line parameters, node information, MATLAB applications programming, a PC; MATLAB programming codes utilizing a Fast-decoupled load flow calculations approach. ETAP programming will be additionally utilized for examination, comparism, and result justification. The FDLF technique was utilized for the study being considered. The system was modeled and demonstrated using the Electrical Transient Analyzer Program (ETAP programming) for simulation purposes employing fast decoupled. The universal purpose NR method of power flow studies was used for solving initial values.

3.1. Power Flow Equations

Sample of Node of a Power System network is as shown in Figure 1(a & b) for illustration purposes.

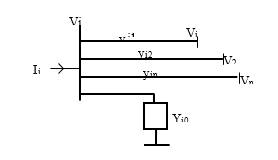
Figure. 1(a): Sample of a Power System Model Bus for the Network

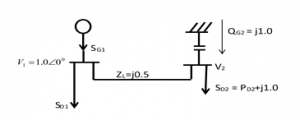
Figure 1(b): Two Bus System Network

The capacitor, in this case, injects a specified power in the system, while the voltage is controlled.

Using Kirchhoff current law (kcl) from Figure 1(b) we obtain

The complex power at node I is given as

Separating real and imaginary parts

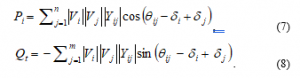
Equations 7 and 8 constitute a set of non- linear algebraic equations in terms of independent variables, voltage values in per unit, and phase angle in radians. Using the Taylor series approach in expanding Equations 7 and 8 with the initial estimate and neglecting all higher-order terms results in a set of equations as shown below:

Table: 1:  33KV Feeders and Injection Substations at port Harcourt Town Zone 4

Port Harcourt Town 33KV Feeder (Amadi Junction-Nzimiro Road)			33/11KV Injection Substations
Fdr S/N	Feeder Name	Installed  Transformer Capacity (MVA)	Feeder Name	Transformer Installed Capacity (MVA)
1	UST feeder	30	RSUST Agip NAOC	2×15 1×7.5 2×3
2	Secretariat Feeder	45	Secretariat Marine Base Juanuta	2×7.5 2×15 1×2.5
3	Borokiri Feeder	60	Borokiri Eastern Bypass	1×15 1×15
4	Silver Bird Feeder		Silver Bird Kidney Island	1×15 1×1.5
5	UTC Feeder		UTC Water Works	1×15 1×15
6	Rumuolumeni Feeder		UOE School of Nursing Naval Base Master Energy	1×7.5 1×15 2×2.5 1×1.5
7	Nzimiro Feeder, etc.	30	Nzimiro-Old Diobu, Owerri Road, etc	3×15

The terms DPi^(k) and DQi^(k) in Equations 9 are the differences between the computed and scheduled quantities, called power mismatch or residual, expressed as in Equations 14 and 15.

3.2. Formulation of Power Flow Equations

A complex unified system with several nodes interconnected through transmission lines can be described as a power system. The load flow issue includes the calculation of voltage values and phase angle at every node, real and reactive power flow in all subsystems in the network under predictable or consistent state condition. Formulation and calculation of node admittance matrix is the starting point in the solution of power flow which is formed from transmission line parameters. In this manner, a contextual analysis is taking from Port Harcourt Town (zone 4) on the 33KV Distribution System of active feeders with 165MVA as a complete installed limit of the Transformers. The breakdown of the distribution transformers added to the incoming substation is as shown in Table 1 while Figure 2 depicts the 33KV Distribution System of the substations used as the case study.

3.3. Line Parameters for Port Harcourt Town, 33KV Distribution Network

Consider the line Parameters of the 33KV Distribution System, the conductors are evenly sorted and are overhead lines.  The spacing between FACT as in the case of the Nigerian 33KV distribution system is 88cm. (that is, D = 0.88m) and. Figure 3 is the phi representation of per phase Line.

For the UST Feeder (33KV) on Node 2 at 15.15km to Incoming Substation; with Conductor Cross-Sectional Area, A = 182mm2ACSR/GZ. (Aluminum conductor steel fortified with electrifies).

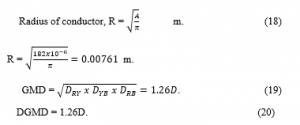
Figure 2: 33KV Lumped Load Distribution Network for Port Harcourt Town (Zone 4) Injection Substation.

DGMD = 1.26 x 0.88 = 1.1088m or 1.109m.

Resistivity of Aluminum,

Figure 3:   П Representation of a Line (Per Phase)

Port Harcourt Town, 33KV Distribution Network, Per-Kilometer Resistance, (R_o) (area A = 82mm² = 182 x 10^-6 m²) using Equation 21,    

b_(UST) = 3.504 x 10^-6 x 15.15km = 53.1 x 10^-6   or siemens

Shunt admittance (susceptance) value for Node 1-2 for UST Feeder Network.

Given b_(UST) = 53.1 x 10^-6 ,

Qc _(UST) = 0.5 x 33² x 53.1 x 10^-6 = 0.0289 MVAr.

Per-Unit Values of the Line Parameters for Port Harcourt Town, 33KV Distribution Network

We compute the complex power demanded at the load side bearing in mind the percentage loading. Note that, the loading capacity is due to available power

Per Unit Load Parameter at Each Feeder for Port Harcourt Town, 33KV Distribution Network

UST Feeder (Node 1-2) for Port Harcourt Town, 33KV Distribution Network

SD = 30MVA, Percentage loading =60%, Pf= cos = 0.8, Rf = sin = 0.6.

SD(1-2) = 30×0.6=18MVA, PD(UST)=18×0.8 =14.4MW, QD(UST)=18×0.6 =10.8MVAr

On 100 MVA base, the per unit values of the complex power demand, we have

Nzimiro-Trans-Amadi Feeder (Node 1-9) for Port Harcourt Town, 33KV Distribution Network

SD = 15MVA, Percentage loading = 80%, Pf = cos = 0.8, Rf = sin = 0.6

SD (1-9) = 15×0.8 = 12MVA, PD (NZ-A.) = 12×0.8 = 9.6MW, QD (NZ-A.) = 12×0.6 = 7.2MVAr

On 100 MVA base, the per unit values of the complex power demand, we have

Nzimiro-Old-Diobu Feeder (Node 1-10) for Port Harcourt Town, 33KV Distribution Network.

SD = 15MVA, Percentage loading = 80%, Pf = cos = 0.8, Rf = sin = 0.6.

SD (1-10) = 15×0.8 = 12MVA, PD (NZ-OD.) = 12×0.8 = 9.6MW, QD (NZ-OD.) = 12×0.6 = 7.2MVAr

On 100 MVA base, the per unit values of the complex power demand, we have

The complex power received from the grid network to the 33KV node is 165MVA at a power factor of 0.8, we have Srec = (130+j100.8) MVA. Where 130MW is the real power and 100.8MVar is the reactive power demanded on the 33kV node.

The summary of the 33kV Distribution node network data under consideration are shown in Tables 2 and 3. It is much better

to compute all other parameters using the per unit values. To realize its real values we multiply the per unit values by the base values assumed at the beginning.

3.4. Mathematical Model of Fast Decoupled Power Flow Method

In a power network, the net infused active and receptive power at an ith node are mathematically represented by:

where Vi and Vj, represent voltage levels at the ith and jth nodes separately; Gij+ jBij is the ijth component of the Y-node; and “n” the entire number of nodes. The linearized power flow Eqns. (26) and (27) are stated or given in reduced forms:

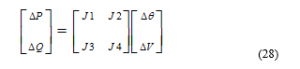
We compute the complex power demanded at the load side bearing in mind the percentage loading.

Note that, the loading capacity depends on the available power.

Table 2:   Line Data for Port Harcourt Town, 33KV Distribution Network

S/No	Feeders	Impedance code	Impedance, Zseries (pu)	Admittance, Y (pu)	Susceptance B/2      (pu)
1.	(Node 1-2) UST	Y1,2	0.2159 + j0.4567	0.8460-j1.7897	j0.0002890
2.	(Node 1-3) Secretariat	Y1,3	0.1452 + j0.3072	1.2576-j2.6607	j0.0001940
3.	(Node 1-4) Silver bird	Y1,4	0.0436 + j0.0922	4.1916-j8.8638	j0.0000584
4.	(Node 1-5) Borokiri	Y1,5	0.1573 + j0.3328	1.1608-j2.4561	j0.0002110
5.	(Node 1-6) UTC	Y1,6	0.0427 + j0.0904	4.2719-j9.0441	j0.0000572
6.	(Node 1-7) Rumuolemeni	Y1,7	0.2565 + j0.5426	0.7120-j1.5064	j0.0003430
7.	(Node 1-8) Owerri Road	Y1,8	0.0003 + j0.0006	666.67-j1333.3	j0.00000038
8.	(Node 1-9) Nzimiro Trans- Amadi	Y1,9	0.0003 + j0.0006	666.67-j1333.3	j0.00000038
9.	(Node 1-10) Old Diobu	Y1,10	0.0003 + j0.0006	666.67-j1333.3	j0.00000038

Table 3: Node Data for Port Harcourt Town (Zone 4), 33KV Distribution Network (Initials Input)

Node	Type	Vsp (pu)	PD (pu)	QD (pu)
1	slack	1.00	0	0
2	PQ	1.00	0.144	0.108
3	PQ	1.00	0.228	0.171
4	PQ	1.00	0.079	0.059
5	PQ	1.00	0.144	0.108
6	PQ	1.00	0.234	0.176
7	PQ	1.00	0.187	0.142
8	PQ	1.00	0.096	0.072
9	PQ	1.00	0.096	0.072
10	PQ	1.00	0.096	0.072

Table 4: Results for the Solutions after Injection of Reactive Power into the Under-Voltage Feeders (ETAP)

Results before Injection of Reactive Power					Results after Injection of Reactive Power
Feeders	Initial Load (Power) Received		Bus Volts  (KV)	% Drop in Volt	Reactive Power Injected	New Bus Volts  (KV)	New Net power Received		% Drop in Volt
	MW	MVar	KV	%	MVar	KV	MW	MVar	%
2	12.8	9.6	29.83	9.61	21.7	32.799	13.6	10.2	0.6
3	20.1	15.1	29.37	11.0	33.8	32.333	23.4	17.6	2.0
5	14.4	10.8	30.60	8.3	19.1	32.261	15.5	11.6	2.2
7	13.9	10.4	28.46	13.9	23.9	32.274	16.2	12.2	2.2

The sub-networks J1 and J4 in Eqn. 28, have a similar order because of the absence of the Q-V equations at PV nodes. A few presumptions are made as in previous studies in the formation of the FDPF model from Eqn. (28) the sub-matrices J2 and J3 are disregarded. Subsequent to joining the assumptions, the subsequent FDPF conditions become:

The suffix “i” represents the ith node, Q-shunts,i; and P-shunts,i are the reactive and real powers, because of lumped shunts at the ith node. It ought to be noticed that the order for the Jacobians  are  (nb-1) by (nb – 1) in Eqns. (29) while that of  in Eqn. (30) is (nb –mb -1) by (nb – mb – 1) where mb is the total number of voltage-controlled nodes. At the point when both  and  are of the similar order of (nb -1), the matrices are real, sparse, and just contain system parameters. These matrices are only factorized once, stored, and are held and  fixed all  through the iteration. The result of Eqns. (29) and (30) are given by Eqn. (32) and (33):

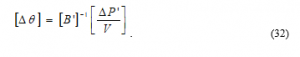
Thus, by utilizing an abridged fast decoupled load flow technique, the voltage values and change in phase angle can be determined.

3.5. Fast Decoupled Power Flow for Radial Distribution System

In the Radial Distribution network, the massive R-X ratio constitutes problems in the convergence of the normal ordinary load flow calculation. Hence, for excellent convergence, some modifications in the load flow methods are applied. The model can be represented by a radial interconnection of networks of the fundamental structure depicted in Figure 4. The dotted lines from the co-generator, shunt capacitor, and load to the ground are to demonstrate that these components might be interconnected in floated delta-design since a given branch might be two-phase or single-phase as situation demands.

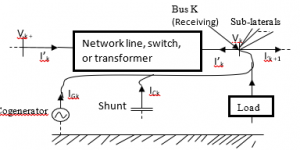
Figure 4: The Building Block diagram of a Radial Distribution System

One of the key ideas driving our techniques is that the current and voltage at one node can be expressed as an element of the current and voltage on the other node. If we let the equation be:

The branch update function [I] is given beneath as:

Where Wk is a vector containing the real and imaginary parts of the voltages and current flows at node k. The factor gk is controlled by the sub-laterals joined at node k like as the models for distribution lines, switches, loads, transformers, co-generators, and shunt capacitors. From Vk we can calculate the flows as a result of the loads, co-generators shunt and, capacitors, given Ik + 1 and the currents Ij taken into sub-laterals branching out from node k, applying KCL at node k to the calculate current [I] given by Eq. 36:

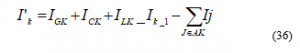
Where Ak is the set of nodes adjacent to node k on sub-laterals.

From Eqn. (36), we calculate the voltage and current at the main side given the voltage and current at the auxiliary or secondary “I” as in Eq. 37:

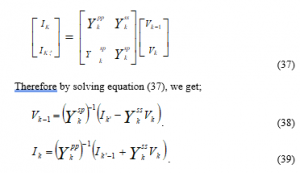
So that by applying this formulation or definition we get the converged values easily and faster than the other normal techniques.

a. Formulation for Fast Decoupled Power Flow Method

The stepwise calculation procedure to solve the power flow issue by applying the Fast Decoupled Power Flow Method is as given in [3] and as summarized thus: Creation of the node admittance Y as indicated by the lines given by the IEEE standard node test system, identification of all kinds of nodes according to the IEEE standard and setting all node initial value of , Creation of the matrices B1 and B11 Where B1 and B11 are the imaginary part of the node admittance matrix of Y_node, Calculating the value DP and DQ  mismatches, Check the convergence status, Calculation of real and reactive power at every node, and checking if MVAr of generator nodes are within the cutoff points, Update of the voltage magnitude V and the voltage angle d at every node. The current can then be determined from the calculated Y node using Eqn. (36)

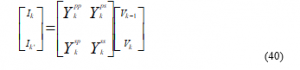
If convergence is attained Display the load flow result, calculation, and show the line flows, current, and losses.

b. Capacitor Bank

Line compensators are introduced in the network because of line losses and other line limitations to reduce losses. In the system under study, shunt capacitors are applied over an inductive load to give part of the reactive VARs required by the load to keep the voltage within the anticipated range. They can also be applied through capacitive loads and in light load situations to consume some amount of the main (leading) VARs for accomplishing voltage regulation. Capacitors are connected either directly to a node or through the tertiary winding of the primary transformer and are installed along the line as to limit mishaps in form of losses, voltage drop, also improves loading power factor. The shunt capacitor banks introduce reactive power into the system and compensate for line losses. To avoid much harmonic in line FACTS devices suffice.

Implementation of the Fast-Decoupled Load Flow in MATLAB. The program is implemented in the MATLAB programming language and is run in MATLAB Software development environment. The software modules files (M-files) results are as presented in appendices A1 to A3:

3. Results and Analysis

The results obtained are shown in Figs 5, 6, A1 to A3, and Tables 4 to 9 using the Fast decoupled-N-R procedures inserted in ETAP programming. The outcomes of the studied power flow and its parameters determined utilizing MATLAB program are represented in Figs. 5, 6, and Tables 4 and 5. The power flow study of the 33KV Distribution system making use of Port Harcourt Town, Zone 4, are presented in appendix A1 to A3 for different results sections from the utilization of the methods and simulation of the system as follows:

Injection of Reactive Power into the Feeder (via Capacitor Bank) using ETAP

Feeder 2 (Node 1-2): The initial net load (Power) received was 9.59 MVAr and 12.76 MW  with a voltage drop of 0. 961. But after injection of 21.67 MVAr of reactive power through a capacitor bank, (Cap 1- rated 22MVAr), the voltage drop reduces to 0.0059 while the new net load (power) became 10.18 MVAr and 13.57MW, new node voltage becomes 0.994 with an angle of -5.48 degree as in Table 4.

Feeder 3 (Node 1-3): The initial net load (Power) received was 15.09 MVAr  and 20.14 MW with a voltage drop of 0.11. But, after the injection of 33.79 MVAr of reactive power, – 0.49MW through a capacitor bank, (Cap 2- rated 35MVAr), and the voltage drop reduces to 0.02 while the new net load (power) became 17.58 MVAr and 23.46MW. The new node voltage becomes 0.9798 with an angle of -6.08 degree. Table 4 shows the summary of reactive power injected into the feeders to improve the voltage profile and the net power received, using ETAP.

Injection of Reactive Power into the Feeder (via Capacitor Bank) using MATLAB

Figure 5: Feeder Power Losses before Injecting Reactive Power (ETAP)

In the new input node data, we have injected reactive power via the capacitor bank. The results are as in Table 5. The values of the reactive power injected were as follows: Node-2 @ 20 MVar, Node-3 @ 30MVar, Node-5 @ 20MVar and Node-7 @ 22MVar. (Check along QGi)

Table 5: New Input Bus Data Injecting Reactive Power (MATLAB)

New Bus Data Input with Capacitor Bank

Bus  Type   Vsp    Theta      PGi       QGi       PLi         QLi       Qmin        Qmax

1       SL     1.00    0.00        0.00     0.00      0.00    0.00     0.00        0.00

2       PQ    1.00    0.00        0.00     20.00    14.40  10.80   -5.00      5.00

3       PQ    1.00    0.00        0.00     30.00    22.80   17.10   -3.00     5.00

4       PQ    1.00     0.00       0.00     0.00      7.90    5.90       0.00     0.00

5       PQ    1.00     0.00       0.00     20.00    14.40   10.80    -5.00    10.00

6       PQ    1.00     0.00       0.00      0.00     23.40   17.60    0.00      0.00

7       PQ    1.00     0.00        0.00    22.00    18.70   14.20   -6.00     15.00

8       PQ    1.00     0.00        0.00     0.00       9.60    7.20     0.00       0.00

9       PQ    1.00     0.00        0.00     0.00        9.60    7.20     0.00       0.00

10     PQ    1.00    0.00        0.00     0.00         9.60    7.20     0.00       0.00

From the voltage profile, the network required more power injection and some tap setting. In Table 7, M means the bus voltage is marginal while C mean critical.

Table 6: Results for 10 Bus/9 Feeder System Load Flow Solutions before Injection of Reactive Power (ETAP)

Bus	Type	V KV	Angle	P. Received PS(rec)    QS(rec)		P. Dispatched Pdisp        Qdisp MW       MVar		Demand -Pnet        -Qnet MW       MVar
1	slack	33.00	0.0	130.001	100.846	–	–	–	–
2	PQ	29.82	-1.5	0	0	13.905	10.940	12.819	9.614
3	PQ	29.65	-1.5	0	0	21.742	17.203	19.949	14.962
4	PQ	32.64	-0.2	0	0	7.886	5.938	7.818	5.863
5	PQ	30.68	-1.1	0	0	14.026	10.894	13.229	9.922
6	PQ	31.89	-0.5	0	0	24.789	18.928	24.122	18.092
7	PQ	27.81	-2.4	0	0	18.851	15.344	16.415	12.311
8	PQ	32.99	0.0	0	0	9.601	7.200	9.600	7.199
9	PQ	32.99	0.0	0	0	9.601	7.200	9.600	7.199
10	PQ	32.99	0.0	0	0	9.601	7.200	9.600	7.199

Table 7: Line Losses and Voltage Drop before Injection of Reactive Power (using ETAP)

Bus	Power Losses PLine           QLine (MW)      (MVar)		Vd % Drop in Vmag.	conditions		Remarks
1-2	1.086	1.325	9.7	9.7% >5%	Under Voltage (C )
1-3	1.791	2.241	11.0	11.0% > 5%		Under Voltage (C)
1-4	0.682	0.747	1.08	1.08% < 5%		Acceptable
1-5	7.974	9.721	8.3	8.3% > 5%		Under Voltage (M)
1-6	6.860	8.485	3.35	3.35% < 5%		Acceptable
1-7	2.436	3.034	13.9	13.9% > 5%		Under Voltage (C )
1-8	0.007	0.008	0.01	0.01%<< 5%		Acceptable
1-9	0.007	0.008	0.01	0.01% << 5%		Acceptable
1-10	0.007	0.008	0.01	0.01% << 5%		Acceptable
Total	6.8502	8.485

Table 8: Summary of the Bus Voltages before and after Injection of Reactive Power (with MATLAB)

Bus Voltage before Injecting Reactive Power				Bus Voltage after Injecting Reactive Power
B/ No	Bus Volt (KV)	Angle (degree)	% Vd	Bus Volt (KV)	Angle (degree)	% Vd
1	33.000	0.000	0.000	33.000	0.000	0.000
2	30.525	-0.043	7.490	33.244	-0.085	0.740
3	31.307	-0.045	5.130	33.085	-0.088	0.260
4	32.716	-0.004	0.860	32.703	-0.005	0.910
5	31.574	-0.030	4.320	33.201	-0.062	0.609
6	32.155	-0.012	2.560	32.119	-0.014	2.670
7	29.651	-0.069	10.15	32.567	-0.123	1.310
8	32.997	-0.000	0.000	32.997	-0.000	0.010
9	32.997	-0.000	0.000	32.997	-0.000	0.010
10	32.997	-0.000	0.000	32.997	-0.000	0.010

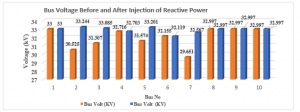
Figure 6: Bus Voltage before and after Injection of Reactive Power

Table 9: Summary of the Net-load/Power and line Losses before and after Injection of Reactive power into Z4 station

Bus Net Load (Power) Received  before Injecting Reactive Power					Bus Net Load (Power) Received  after Injecting Reactive Power
B/No	PNet (MW)	QNet (MVa)	Line Loss (MW)   (MVar)		PNet (MW)	QNet (MVar)	Line Loss (MW)       (MVar)
2	14.400	10.774	0.7657	1.6197	14.400	9.229	0.62241	1.31659
3	22.800	17.083	1.3094	2.7704	22.800	12.920	0.99193	2.09863
4	7.900	5.894	0.0398	0.0842	7.900	5.894	0.04313	0.09120
5	14.400	10.780	0.5302	1.1217	14.400	9.221	0.45441	0.96139
6	23.400	17.594	0.3557	0.7530	23.400	17.595	0.38635	0.81795
7	18.700	14.172	1.7492	3.7003	18.700	7.833	1.08263	2.29020
8	9.602	7.201	0.0004	0.0008	9.604	7.196	0.00042	0.00086
9	9.602	7.201	0.0004	0.0008	9.604	7.196	0.00042	0.00086
10	9.602	7.201	0.0004	0.0008	9.604	7.196	0.00042	0.00086
Total	130.406	97.9	4.7512	10.0517	130.412	84.28	3.58212	7.57854

4. Discussion

Power flow is a significant and fundamental device for the study of any power system and also applied in the operation, arranging for future development/upgrade of power systems. It will help in deciding the best mode of operation of the existing networks.

The results of the voltage values in nodes, 2, 3, 5, and 7 were not within the acceptable range because its node voltage was critical while node 6 is marginal and is within the required range. The steady-state MW and MVAr delivered to the slack node is not

equal to the sum of the load (Power) demanded at each node. The transmitted/injected power and the power expected/net power at the load point were not equal, due to power losses on each feeder. The total disposable power received was 129.741 MW and 83.818 MVAr with Fast Decoupled Newton-Raphson technique in MATLAB Environment after incorporation of Capacitor bank to the nodes that were influenced by unsatisfactory voltage drop, while the entire net load got using ETAP programming was 92.782 MVAr and 125.765 MW.

The Voltage drop at Node 6, 8, 9, and 10 are within the acceptable range. These nodes Voltage drops are less than or equal to the acceptable 0.05 of the nominal voltage drop. Figure 6 above, shows the Node Voltage profile before and after the injection of Reactive Power.

The total power (line) losses on the feeders have been reduced from 10.05MVAr and 4.75MW to 7.57MVAr and 3.58MW. This gives 0.246 reductions of the entire real power loss after the addition of reactive power into the black nodes.

5. Conclusion

The analysis of this work has revealed the areas of consideration and urgent attention. The use of Fast Decoupled Load Flow study with MATLAB and the use of ETAP programming helps the examination precisely and proactive with less need for memory space. The load dispatched from the grid system to the transmission substation was not satisfactory thus every receiving substation has a fraction of sharing the available power or load.

The simulated results show that more power is required from the grid network to the receiving substations through the Port Harcourt Town (Z4) control transmission center. In this way, without a satisfactory power source from the grid system, alternative energy supply or distributed generation suffices or, calls for load shading as the only way out.

The entire power losses adding up to 10.05MVAr and 4.75MW on the 33KV distribution system require the update of the system by distributing or adding more load from the grid to these essential distribution centers, or alternative power generation should be sourced to beef up else load shedding becomes the only option.  However, the recommendation and installation of the line compensator as “ccapacitor bank” at the affected nodes improved the voltage profile. Giving a 0.246 decrease in real power loss when capacitor banks were introduced on problem nodes for better enhancement.

5.1. Recommendations

1. We recommend that the 33KV distribution system be made more reliable by increasing the number of protective elements, capacitors banks, and transformers as realized from the results obtained. Also, intermittent power flow analysis and maintenance should be carried out.
2. The reactive power required locally at the nodes can be utilized to limit or minimize the losses on the line related with the system.
3. The substations for the network in this study should be made to perform at least 20 to 25 percent below the supply power to the secondary distribution system.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

My warm appreciation & respect to all the staff of the Port Harcourt Electricity Distribution Company of Nigeria (PHEDC), Moscow Road, Port Harcourt; all staff of Transmission Company of Nigeria, Port Harcourt Zone, for making this research work a worthwhile success. My sincere appreciation also goes to all the members of N.S.E and staff of the Rivers State University, Port Harcourt. My inmost sincere thanks to the African Centre of Excellence for Sustainable Power & Energy Development (ACE-SPED) University of Nigeria, Nsukka, Enugu State, Nigeria.

1. I.A. Adejumobi, G. A. Adepoju, and K.A. Hamzat, “ Iterative techniques for load Flow Study: A Comparative Study for Nigeria 330KV Grid System as a Case Study” International Journal of Engineering and Advanced Technology (IJEAT) ISSN: 2249-8958, 3(1), October 2013
2. C.S Indulkar and K. Ramalingam “Load flow Analysis with voltage-sensitive loads” Joint International Conference on Power System Technology and IEEE Power India Conference 2008
3. H. K. Okyere, H. Nouri, H. Maradi and Li Zhenbiao “ Statcom and load tap changing transformer (LTC) in Newton Raphson Power Flow: Bus voltage constraint and losses” 42nd International Universities Power Engineering Conference 2007
4. M. Sailaja Kumari and M. Sydulu “ A fast and reliable quadratic approach for Q-adjustments in Fast M Applied to power systems, 2006
5. J. Nanda, V. Bapi Raju, P.R. Bijwe, M. L. Kothari and M. Joma “New findings of convergence properties of fast decoupled load flow algorithms”, IEE Proceedings C- Generation, transmission and Distribution, 1991
6. T. Ochi, D. Yamashita, K. Koyanagi, & R. Yokoyama, “The Development and Application of Fast Decoupled Load Flow Method for Distribution Systems with High R/X Ratios Lines”, In 2013 IEE PES Innovative Smart Grid Technologies Conference, Washington DC, USA. Retrieved from https://waseda.pure.elsevier.com. 25th, July 2016.
7. F.S. Abu-Mouti, & M.E. El-Hawary, A New and Fast Power Flow Solution Algorithm for Radial Distribution Feeders including Distributed Generations”, Institute of Electrical & Electronics Engineering Transactions on Power Systems, 2668 – 2672, 2007.
8. B. Stott and O. Alsace “ Fast Decoupled Loaf Flow” IEEE Transaction on Power Apparatus and Systems, PAS-93, 1974
9. G. B Jasmon and L.H.C. C Lee, “ Stability of Load flow techniques for distribution system voltage stability analysis”, IEE Proceedings C- generation transmission and Distribution, 138(6), 479-484, Nov 1991
10. A. Sharma, Deep Kiran and Bijaya K Panigrahi, “ Planning the coordination of overcurrent relays for distribution systems considering network reconfiguration and load restoration”, IET Generation, Transmission and Distribution, 2018
11. P. S. Bhowmik, S. P. Bose, D. V. Rajan, and S. Deb, “Power flow analysis of power system using power Perturbation method” IEEE Power Engineering and Automation Conference, 2011
12. H. M. Gibson Sianipar, Giri Angga Setia and M. Fatahillah Santosa, “Implementation of Axis Rotation fast Decoupled Load Flow on distribution systems” 3rd conference on power Engineering and Renewable Energy (ICPERE), 2016
13. R. Mageshvaran, R.I. Jacob, V. Yuvaraj, P.Rizwankhan, T. Vijayakumar, & V. Sudheera, , “Implementation of Non-Traditional Optimization Techniques (PSO, CPSO, HDE) for the Optimal Load Flow Solution”, TENCON 2008 – 2008 IEEE Region 10 Conference, 19-21.doi:10.1109/tencon.2008.4766839, 2008.
14. S. Vasanthara, “Electric power systems” Electric renewable Energy Systems, 2016
15. W. Xi-Fan, Song, Yonghua and Irving Malcolm “Modern Power System Analysis”, (3rd ed.), New York: Mc-Graw-Hill, 2008.
16. H. A. Raza et al., “Analysis the effect of 500kv High-Voltage Power Transmission Line on the Output Efficiency of Solar-Panels,” in 2019 International Conference on Electrical, Communication, and Computer Engineering, 1–6, 2019. doi: 10.1109/ICECCE47252.2019.8940803.
17. H. D. Chiang, “A decoupled load flow method for distribution power network algorithms analysis and convergence study”, Electric Power Energy System, 3(3), 9-13,1991
18. M.S. Srinivas, “Distribution load flows: A Brief Review”, IEEE Power Engineering Society Winter meeting 2000, 2, 942-945,2000
19. S. M. Lutful Kabir, A Hasib Chowdhury, Mosaddequr Rahman and
20. J. Alam “Inclusion of slack bus in Newton-Raphson load flow study” 8th International Conference on Electrical and Computer Engineering 2014

(Click Here)

(Click Here)