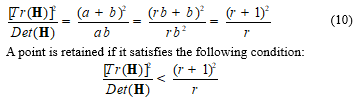1.Introduction

The detection and the description of stable local features are two fundamentals components of many object recognition algorithms. In this context, Moravec and Harris were the first who proposed algorithms for the detection of interest points. Over time, several improvements have been applied to these algorithms until the appearance of the SIFT algorithm. This was a big success in various applications of computer vision.

In the computer vision field, it is interesting to extract features of an image for use in various applications such as image recognition, autonomous navigation of robots, and face recognition.

A significant progress has been developed in this axis. One of the most interesting works of characterization that gives good results was carried out in 2004 [1]: Features extracted by SIFT (Scale Invariant Feature Transform) are largely invariant to rotation, change of scale, change illumination, noise and small changes in views.

The main disadvantage of the SIFT algorithm is its high computational cost. This is the result of the complex iterative process used to obtain the invariance to changes and transformations mentioned above. An effective solution to this problem is to move to embedding this algorithm on hardware platforms, to improve the execution time.

In the second section of this paper, related works are presented. Section 3 shows briefly explanation of the principles of SIFT algorithm. In section 4, proposed method is developed. The experimental results are shown in Section 5, and a conclusion summarizes proposed work and suggests some ways to improve results.

2. Related works

The SIFT algorithm has succeeded in a large number of applications; however, its high computational complexity has been a challenge for embedded implementations. Several works have overcome this problem while developing hardware architectures based on very powerful development platform, which allows improving the running time and the precision of the results. In fact, they have benefited from the hardware parallelism offered by (Field-Programmable Gate Arrays) FPGAs. Some studies have only implemented the detection portion of points of interest based only on a purely hardware architecture. Other works are based on a mixed architecture (hardware /software), where the software part is designed using a softcore (Nios II) or a Digital Signal Processor (DSP). A full hardware implementation was presented in 2008 [2].

The author proposed a parallel hardware architecture for detecting of points of interest based on the SIFT algorithm applied to the Simultaneous Localization and Map-building (SLAM) problem. That architecture was based on specific hardware optimizations considered fundamental to include such a robotic control system on a chip. The proposed architecture was completely independent and able to detect features from 30 images/second. They calculated the descriptor through the Nios II processor. Another architecture was proposed in 2009 [3]. Authors modified the original version of the SIFT algorithm to increase the processing speed and reduce the used hardware resources. They used two octaves where each one was formed by four scales, instead of three octaves each one was formed by five scales. This choice has degraded the mapping results, but it has optimized the use of material resources. They also reduced the size of the descriptor, in order to reduce the execution time; they went from a size of 128 to a size of 72. With this optimization, the proposed system was able to detect the features of an image of a size of 640 ´ 480 pixels in 31 milliseconds. In [4], the authors presented a partial implementation of the SIFT algorithm, where they only implemented a feature extraction part. The proposed architecture is able to detect points of interest from an image of 320 × 240 pixels in 11 ms.

In [5], the author described a low-cost embedded system based on a new architecture that successfully integrates an FPGA and a DSP. The step of detecting characteristics was implemented using a fully parallel architecture based on FPGA. However, the description step was performed using a fixed-point DSP.  With this new design, it allowed both reducing the used hardware resources and to accelerating treatment. It was able to detect characteristics in 10ms from images of a size of a 320 ´ 256 pixels (without convolution step). Despite the optimizations made by the authors during the design of their architecture, the latter mismatched compared with the result obtained by the executable in [6]. This defect was caused by the loss in accuracy due to the representation of the data relating to the magnitudes and orientations in a fixed point format.

All these works have benefited from hardware parallelism offered by FPGAs to optimize the computation time and increase accuracy. But the developed architectures are dedicated to a very specific FPGA [2], [7], [8] and if you want to change the target FPGA card, you must make changes that can take a lot of time; as the example of [2] where architecture will be implemented on the FPGA of the Altera family. This paper presents a partial implementation of the SIFT algorithm, which is to implement just the extraction of the characteristics that is based on the LEON3 processor. This implementation method overcomes the existing problems in the methods presented above. Indeed, the high flexibility of the processor allows the possibility to develop the application independent of the target board.

3. Description of SIFT Algorithm

The SIFT algorithm was proposed in 2004 [1], it has been used mainly in the field of computer vision for recognizing object, people and faces. This algorithm is decomposed into four parts:

• Detection of extrema in the scale space
• Precise localization of points of interest
• Assignment orientations
• Descriptor Calculation

In this article, only the first and second step of the algorithm are considered.

3.1. Detection of extrema in space scales

This step is to determine the location of the invariant point scale change through a continuous scaling function called scale space. This function was provided in 1984 [9]. In fact, it is the result of the convolution of the Gaussian function G (x, y, σ) with an I (x, y) input image:

After determining the scale space, Lowe proposed to calculate the difference of the Gaussian (DOG) to determine the points of interest invariant to scale changes. Unlike the Gaussian is calculated from the difference between two adjacent scales separated by the constant factor k.

         (3)  Below is a detailed demonstration of this approximation:

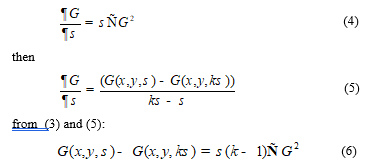The factor (k–1) in the equation is a constant that affects neither the location nor the stability of the points of interest.

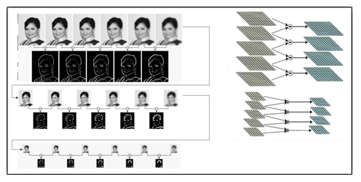Figure 1:  Detection of extrema in space scales: steps of forming the pyramid

The above steps will form a single octave. However, Lowe proposed to determine the point of interest within a pyramid which is a set of octaves. So, to form a new octave, it reduces the size of the original image of the previous octave and the process is repeated. Figure 1 shows the steps of forming the pyramid. Indeed, the original image is sampled down by a factor of two, and then by a factor of four in order to form the basic image of each octave. Then, inside each octave, the initial image is convolutional   with a Gaussian is to produce all the images of the scale space. Finally, the adjacent images of the same octave are subtracted to produce difference of Gaussian (DOG).

To detect the local maxima and minima of D(x, y, σ), each point is compared with its eight neighbors in the current image and the scale in its nine neighbors in the above and below scales. It will be chosen only if it is larger or smaller than all of these neighbors. Figure 2 shows a detailed explanation of this step.

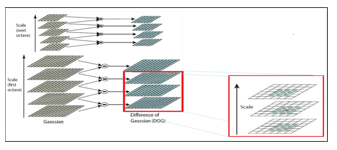Figure 2: Detection of extrema in space scales: detailed explanation

3.2. Precise localization of points of interest

The previous step has generated a set of points, some of which are unstable. For this, an elimination should be performed for low contrast points and points situated on the edges because they are unstable. To eliminate weak points of contrast, the Taylor expansion to order one of the DOG functions is performed. A point of interest is considered unstable if          D(X) < 0.03. A point of interest that is located in the edges is removed if the primary curve along the contour of which it is positioned is greater than the curvature in the orthogonal direction. The main curve is represented by the eigenvalues of the Hessian matrix H of 2´2 sizes given by the following expression:

To avoid the calculation of eigenvalues, users exploited, in general, the approach proposed by Harris and Stephens (1988). Let α is the largest eigenvalues and β the smallest:

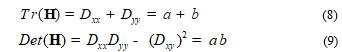 Let r be the ratio between the two eigenvalues (α = rβ), using two expressions (8) and (9), then:

4. Proposed Method

To implement the feature extraction part, a C code is developed which allows the creation of space DOG space and extract the features of an image of a size of 256 ´ 256 pixels. The code is developed in accordance with the original version of the SIFT algorithm, where there is three octaves and where each consists of five scales. Also, a Gaussian filter with size 7 ´ 7 is used. This code is implemented on the FPGA cyclone that hosts the LEON3 processor.

4.1. LEON3 processor

LEON3 [10] is a 32-bit RISC processor provided as a synthesizable VHDL model on digital ASIC or FPGA circuits. The model is highly configurable. In fact, the user can set many features of LEON3 according to his needs. The LEON3 version can be used under the GPL, allowing free use for research. ASIC LEON3 versions have been developed specifically to operate ionizing medium VHDL model and a fault tolerant LEON3-FT. Figure 3 shows the architecture of the LEON3 processor which is formed by two separate and reconfigurable cache instruction and data, 7 pipeline stages, and cabled MAC unit, multipliers and dividers. LEON3 is supplied with an IP grouped together in the “GRLIB IP” library [11] which includes a set of VHDL libraries from which the cores (IP) are instantiated in a local design. The architectures provided by this library are based on the AMBA (Advanced Microcontroller Bus Architecture) bus. There are two distinct types of buses at the AMBA. The AMBA / AHB bus used for the interconnection between the IP that requires a high data throughput as the LEON3 processor, the memory controller and the JTAG. The AMBA/APB bus (AMBA Advanced Peripheral Bus) on which the units that require a low data rate as timers and UART connect. These two buses are interfaced through the AHB/APB Bridge. Furthermore, it contains several LEON3 models designated for different FPGA board. This ensures the LEON3 processor great flexibility. The GRLIB also contains a configurable design for a multiprocessor architecture based on the LEON3. LEON3 makes available to the designer tools facilitating its rapid development (e.g.; through graphical configuration utility). This prevents wasted time in an arduous and time consuming development. For embedded applications, it is fully synthesizable, and can be implemented with a number up to 16 hearts.

4.2. Development platform

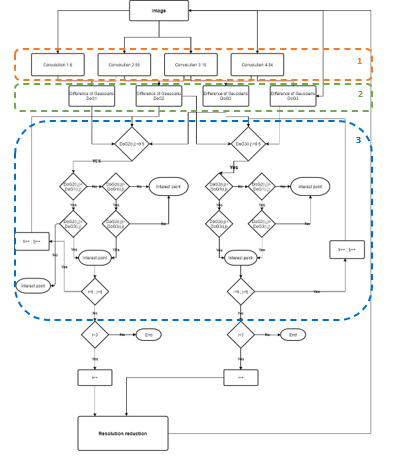
NIOSII is a dedicated embedded hardware platform application. Figure 4 shows the development platform, which is formed equipped with a EP1C20400C700 FPGA. It is also equipped with a set of memory media: flash memory (8 Moctet) SRAM (1 MB) and SDRAM (16 Moctet). In addition, this kit includes a set of communication tools: JTAG, two serial communication ports. Figure 5 shows algorithm flowchart. Step 1 presents convolution product computing. Step 2 compute the difference of Gaussians DoG. Finally, step 3 is dedicated to interest point extraction.

5. Test and verification

To test proposed approach, LEON3 processor should be configured ; this step can be performed either under UNIX or Windows with Cygwin. Then the VHDL code of the processor is compiled in the Altera Quartus environment and finally the transfer to the card is done using the Altera programmer. Now to transfer the code to the card and run it by the LEON3 processor the GRMON tool [12] is employed, this is a debug monitor used for debugging SoC based on the LEON3 processor. The latter supports the following debugging interfaces: UART, PCI, JTAG and Ethernet. JTAG is selected for this step.

Figure 3: Architecture of the LEON3 processor

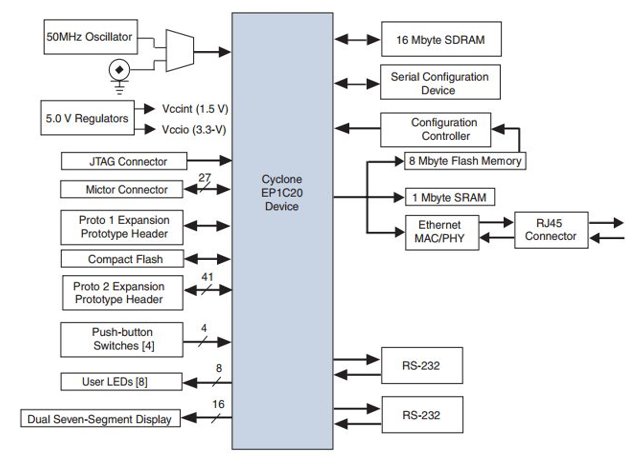Figure 4:  Development platform

Figure 5:  Algorithm flowchart

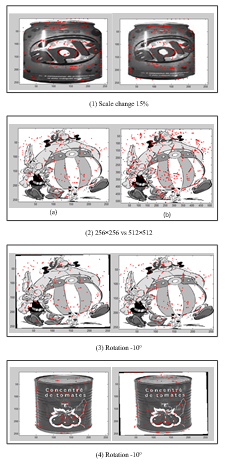Figure 6: Experimental Results

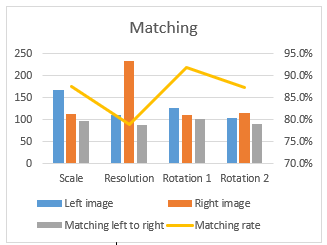
For validation, proposed algorithm is performed on a set of images that have undergone various transformations such as: scaling, rotation, brightness and also images that are taken randomly from the internet. The test results are given in Figure 6. To judge the results; a visual inspection as well as quantitative measures are used. The objective of this evaluation is to locate points of interest on the same position at the same image that undergoes different processing. All these tests confirm that have been able to successfully implement the detection points of interest. SIFT code is running on the FPGA card reliably, but with an execution time equal to 3.06mn. To reduce the execution time, we benefit from a high configurability offered by the LEON3 processor that allows us to quickly design a multiprocessor architecture. This approach consists in subdividing the image into a set of blocks where each block will be executed by a single processor. Thus the run time is equal to the time taken by one processor to determine the points of interest at a single block. The Convolution was included. Process input was a grey level image and process output was SIFT points coordinate. Point description was not included (vector with 128 values) as like the majority of similar work. Embedded code stops at the generation of points. To validate this approach image is divided into four blocks, each of a size of 64 ´ 64 pixels. Where the execution time becomes 9s instead of 3.06 mn. It is to be mentioned that at this article we have used the FPGA Cyclone I, whereas nowadays the FPGA cards are performed in terms of frequency and the number of logical blocks programmable this card as Cyclone III, Vertex V, etc…. In fact, the use of this card increases over the size of the LEON3 processor cache hence reducing memory access time and thus decreasing the execution time. Figure 7 and Figure 8 show statistical result of the detection process as well as matching rate results. Matching rate is computed by dividing number of matched points by minimum between right and left detected points. Obtained rate allows any ego-motion model estimation using rejection sampling for example. It can be used as a recognition support as well.

Figure 7: Number of SIFT detected points

Figure 8: Matching rate

6. Conclusion

The objective in this work is to establish a detailed study of the SIFT algorithm and to propose a solution to implement it on a reconfigurable platform. This paper presented the different methods of extracting and describing points of interest, before focusing the study on the SIFT algorithm. SIFT is characterized by a very high algorithmic complexity due to the intensive use of iterative operations in order to guarantee invariance to the different types of change Rotation, scale …, etc.

Thus, a new method was proposed based on LEON3 which has enabled us, through software programming in C language, to embed the part of extracting points of interest on an FPGA platform. Once the method is implemented, its validation will take place while being based on multiple images. The proposed approach showed very encouraging results.

In order to improve obtained results, a number of perspectives can be considered. In order to increase the size of the processor cache, FPGA boards which have a high integration capacity such as Virtex V, startixII can be used. In order to embed the FPGA platform supporting the SIFT algorithm on board a mobile robot, we propose to refine the results of the point of interest extraction step and program the description part. The main objective still to guarantee the robot’s autonomous navigation (trajectory monitoring, obstacle detection, SLAM…etc.).

1. D. G. Lowe, “Distinctive image features from scale-invariant keypoints”, International Journal of Computer Vision, 60, 91–110, 2004, doi: 10.1023/B:VISI.0000029664.99615.94.
2. V. Bonato, E. Marques, G. A. Constantinides,”A parallel hardware architecture for scale and rotation invariant feature detection”, IEEE Transaction Circuits and Systems for Video Technology, 18(12), 1703-1712, 2008. doi: 10.1109/TCSVT.2008.2004936
3. L. Yao, H. Feng, Y. Zhu, Z. Jiang, D. Zhao, W. Feng, “An architecture of optimised SIFT feature dection for an FPGA implimentation of image processing”, in 2009 International Conference on Field Programmable Technology, 30-37, 2009, doi: 10.1109/FPT.2009.5377651.
4. L. Chang, J. H. Palancar, L. E. Sucar, M. Arias-Estrada, “FPGA-based detection of SIFT interest keypoints”, Machine Vision and Applications, 24 (2), 371-392, 2013, doi: 10.1007/s00138-012-0430-8
5. S. Zhong, J. Wang, L. Yan, L. Kang, Z. Cao, “A real-time embedded architecture for SIFT”, Journal of Systems Architecture , 59(1), 16-29, 2013, doi: 10.1016/j.sysarc.2012.09.002
6. SIFT demo program. www.cs.ubc.ca.
7. S. A. Li, W. Z. Pan, C. C. Hsu, C. K. Lu, “FPGA-based hardware design for scale-invariant feature transform”. IEEE Access, 6, 1-1, 2018, doi: 10.1109/ACCESS.2018.2863019.
8. J. J. Koenderink, “The structure of images”. Biological Cybernetics. 50, 363-370, 1984, doi: 10.1007/BF00336961
9. A. Fejér, Z. Nagy, J. Benois-Pineau, P. Szolgay, A. de Rugy and J. Domenger, “FPGA-based SIFT implementation for wearable computing”, in 2019 IEEE 22nd International Symposium on Design and Diagnostics of Electronic Circuits & Systems (DDECS), Cluj-Napoca, Romania, 1-4, 2019, doi: 10.1109/DDECS.2019.8724653.
10. LEON3 processor. www.gaisler.com
11. GRLIB IP Library User’s Manual [online]. www.gaisler.com
12. GRMON Evaluation version [online]. www.gaisler.com

(Click Here)

No. of Downloads Per Month

No. of Downloads Per Country