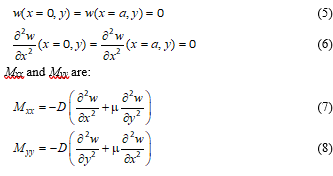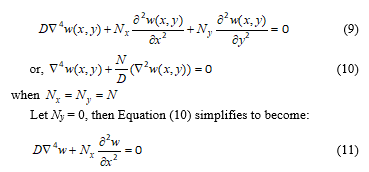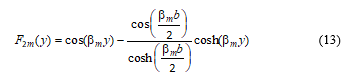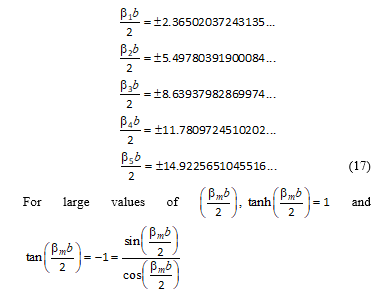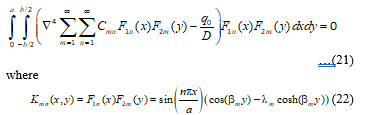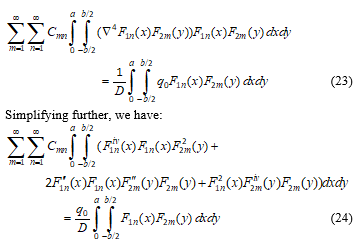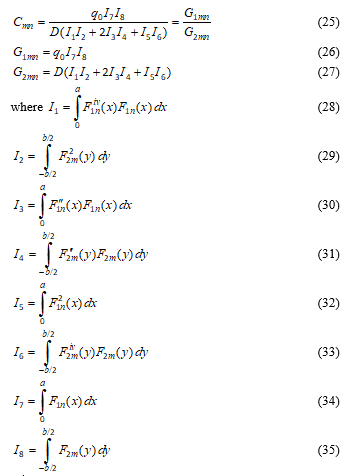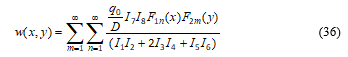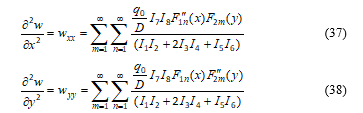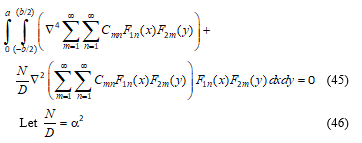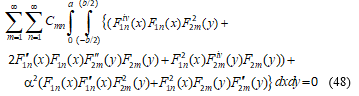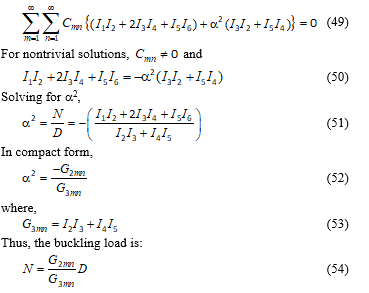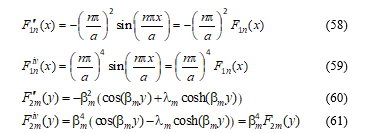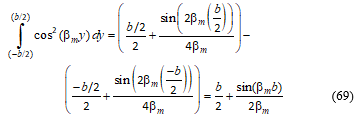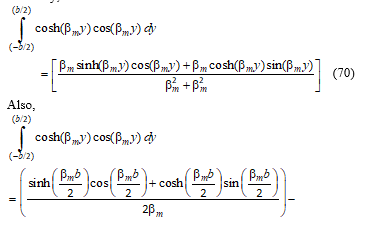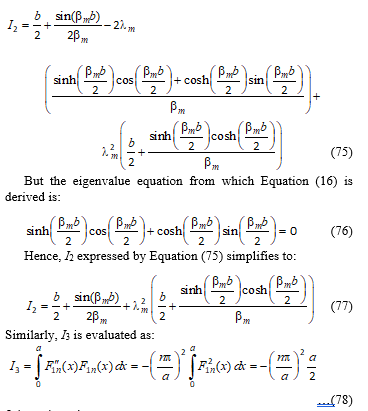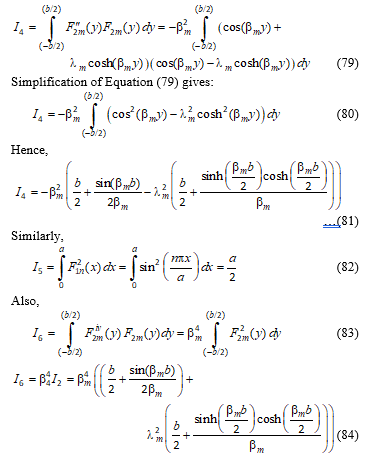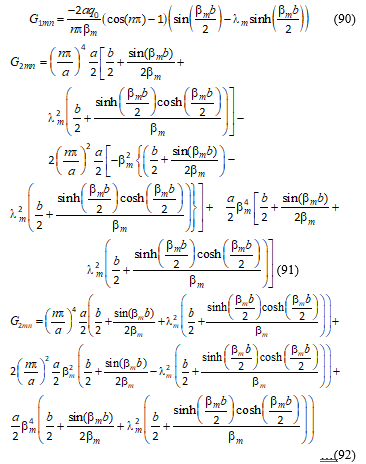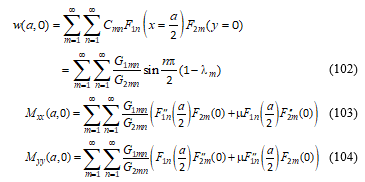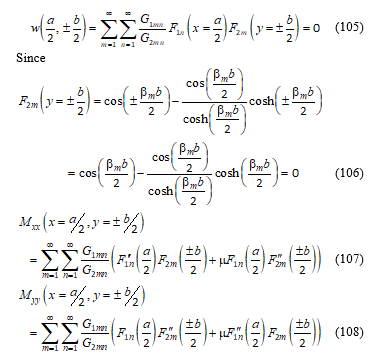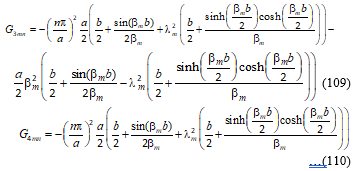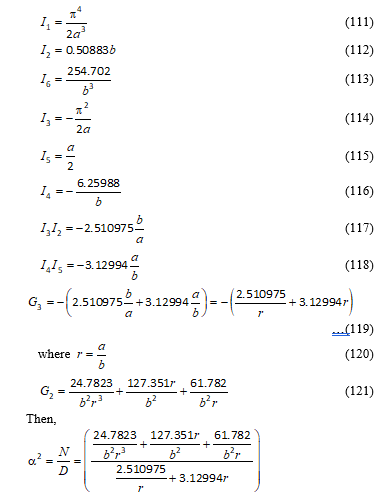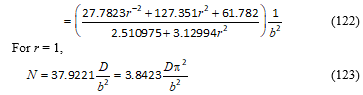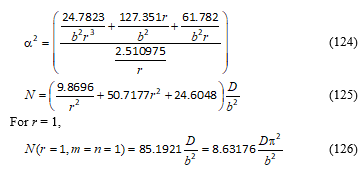1.Introduction

 Plates can be defined as structural members with inplane dimensions of length and width and transverse dimension of thickness where the least inplane dimension is usually much greater than the thickness. Plate problems are thus three-dimensional (3D) problems of elasticity for dynamic, static or stability cases [1–6]. The behaviour and classification of plates depend on the ratio of the transverse dimension and the smaller inplane dimension of the plate. They can be categorized as thin, moderately thick and thick plates. In thin plate, which is the subject of this study the ratio of the transverse dimension to the least inplane dimension is usually smaller than 1/20.

Under certain simplifying assumptions and hypotheses, the theories of plates have been approximated using two-dimensional (2D) idealizations and classical examples are the thin plate theories [1–6]. Plates are applied extensively in the varied fields of engineering and used in civil, mechanical, aeronautical, naval, spacecraft and structural components. This has resulted in the extensive studies done by many previous scholars on the subject matter [1–10]. Plates are subject to loads that produce dynamic flexural, static flexural, and buckling responses. Plates are categorized by using geometries  as rectangular, square, skew, triangular, trapezoidal, sector, circular, elliptical, polygonal, quadrilateral, rhombic; and by their material properties as heterogeneous, homogeneous, anisotropic, orthotropic or isotropic.

This work considers rectangular thin plates made with isotropic, homogeneous, linear elastic materials.

1.1. Theories of plates

Several theories have been derived and developed for plates subjected to flexure and buckling loads [11–17]. Kirchhoff’s (classical small deformation thin) plate theory (KPT) used the following assumptions/hypotheses:

(i)   Cross-section planes that are orthogonal to the plate’s mid-plane prior to loading and bending would continue to be plane and orthogonal to the mid-plane. This is called the normality or orthogonality requirement.

(ii)  The thickness remains unchanged during the bending deformation.

The merits of the KPT are:

(i)   The equation of equilibrium that governs the problem is a linear equation.

(ii)  The governing PDE is expressed in terms of the unknown displacement field in the transverse direction which is found by solving the linear PDE.

(iii)  Bending moments and shear force expressions can be found from the transverse displacement using the equations that relate bending moment to transverse deflection, and equations that relate the shear force to transverse deflection.

(iv) The KPT results in parabolic distribution of shear stresses t_yz and t_zx over the thickness, and this agrees with results from structural mechanics.

The demerits include: (i) the limitation of the KPT to small deformations and (ii) the inability of the KPT to cater for transverse shear deformations, thus limiting the scope of application of the KPT to thin plates; for which transverse shear deformations are negligible.

In [11], the author presented the domain PDE for variable thickness thin plate theory. Few problems of plates with variable flexural rigidity have been solved using analytical methods. Large deflection thin plate theory was developed by von-Karman, as a system of equilibrium and compatibility equations.

Reissner derived a stress-based theory for analysing moderately thick plates by the use of Castigliano’s theorem resulting in a system of three PDEs. In [3] the author derived a first order shear deformation plate theory (FOSDT). The theory considered transverse shear deformation effects by assuming linear variations across the thickness for the three displacement components. The governing PDE of Mindlin plate theory are a set of three coupled PDEs in terms of three unknown displacements w, q_x and q_y where w(x, y) denotes deflection in the transverse coordinate, q_x and q_y are the rotations of the plate mid-plane (z = 0).

In [18], the authors presented flexural solutions for thin plates subjected to linear variations of transversely applied loading. In  [19] the author used the Vlasov variant of Galerkin’s methodology to present a bending solution to thin plate resting on one parameter foundations where the plate is submitted to applied loading. In [4] the authors deployed a Vlasov modification of the Galerkin method to the bending problem of rectangular thin plate under uniform distribution of transversely applied loading over the entire plate domain.

In [7], the authors have deployed the Galerkin-Vlasov technique for bending analysis of thin plates with opposite edges fixed and the other edges on simple supports. In [20] the authors have also applied the Galerkin-Vlasov methodology for obtaining solutions to the natural vibration equation of thin plates having simply supported boundaries and obtained the eigenfrequencies and vibration modal shape functions.

Ritz variational methodologies has been deployed for the formulation and solution of classical Kirchhoff plate problems by  authors in [21-23].

In [21], the authors deployed Ritz technique for finding solutions to the bending analysis of rectangular Kirchhoff-Love plates subject to transverse hydrostatically varying loading distributions over the plate region. In [22], the author presented systematically the Ritz method for the flexural analysis of simply supported rectangular Kirchhoff plates under distributed transverse loadings. Similarly, in [23], the author used Ritz technique to solve the bending problems of rectangular thin plates resting on one parameter foundations, with the plate subject to uniformly distributed loading over the entire domain.

Shear deformation theories of plates have been formulated by authors in [2], [24] and [25] amongst others to incorporate the transverse shear stresses and strains on their bending, dynamic and stability behaviours.

1.2. Review of solution methods for plate problems

Plate problems of dynamic and static bending and stability have been analysed using numerical and analytical methods by several researchers.

In [1], the author obtained an infinite series solution to the small displacement bending problems of CSCS (or SCSC) rectangular thin plates subject to uniformly distributed loading, by using the superposition principle to the solution for simply supported plates carrying uniform transverse distribution of loading and the solution to the same problem under an applied torque distribution along the clamped edges where the applied torque is of such a magnitude that rotations vanish at the clamped edges.

Integral transform methods were used for determining problems of thin plates under bending deformations by authors in [10] and [26].

In [8], the authors used the finite Fourier sine transformation methodology for flexural analysis of thin plates resting on one parameter foundations. In [26], the author presented the bending solutions of thin plate supported/resting on one-parameter discrete model of Winkler with the aid of finite Fourier sine transformation technique. In [27], the author presented two-dimensional Fourier cosine series technique to solve bending problems of rectangular thin plates supported by Winkler one-parameter foundations with the plate domain subject to transverse loading.

Kantorovich-Vlasov method was used for the thin plate flexure problems by authors in [9], [28]-[31].

In [9] the authors have studied the use of Kantorovich-Vlasov method for solving bending problems of thin plate with Dirichlet conditions under uniformly distributed transverse loading. In [28], the author presented a mixture of Kantorovich, Euler-Lagrange and Galerkin’s techniques and used it for solving bending problems of rectangular thin plates. In [29], the authors used the Kantorovich method to perform natural transverse vibrational analysis of rectangular Kirchhoff plates, thus obtaining the natural frequencies of transverse vibration. In [30], the authors used the Kantorovich-Vlasov methodology for solving the flexural problems of rectangular Kirchhoff plates with opposite sides fixed, and the other two sides simply supported; with the plate subject to distributed uniform loading. In [31], the authors used the Kantorovich method to solve flexural problems of Kirchhoff-Love plates having two sides fixed and the other sides on simple supports.

Thick thick plates modelled using FOSDT and Mindlin plate theories were studied by authors in [5], [12-17].

Elastic stability problems involving rectangular Kirchhoff plates subjected to inplane compressive loads were investigated by authors in [32-36].

In [32], the authors used the two-dimensional finite Fourier sine integral transformation technique for solving the elastic buckling problems of simply supported rectangular thin plates. In [33], the authors used the one-dimensional (single) finite Fourier sine integral transform method for the elastic stability solutions of thin plates simply supported at two opposite sides and fixed along the remaining two sides for uniaxial uniform compression. In [34], the authors used the Galerkin-Kantorovich technique for the elastic buckling analysis of thin rectangular shaped plates with two opposite sides simply supported and the other two sides fixed (SCSC plates). In [35], the authors used the Galerkin-Vlasov variational method for solving the elastic problems of rectangular thin plates with two types of boundary constraints namely: (a) simply supported on two opposite sides, clamped along the third side and free along the fourth side (SSCF plates). (b) simply supported along the four sides (SSSS plates). They obtained for each considered case, closed form solution that satisfies the boundary conditions and domain equation. In [36], the authors performed and obtained stability solutions for rectangular thin SSCF and SSSS plates using the single finite Fourier sine integral transform method. They obtained for the studied problems, exact solutions that satisfied the deformation and force equations at the restrained boundaries and the governing field equation.

In [37], the authors presented the flexural analysis of annular plates using the indirect Trefftz boundary method. They based their formulation for thin and thick plates on the Kirchhoff classical thin plate theory and the Reissner stress based thick plate theory respectively. They adopted the Trefftz method for their analysis because the Trefftz method uses complete set of solutions satisfying the governing fourth order PDE of the KPT classical thin plate theory and the sixth order PDE of the Reissner plate theory. Another fundamental merit that informed their use of the Trefftz method is that the method avoids singular integrals due to the properties of the solution coordinate functions. They adopted the method because the boundary conditions are automatically considered by the method, rendering the method effective compared with other methods. They solved illustrative problems by the method to demonstrate its effectiveness.

In [38], the authors demonstrated the use of the finite integral transformation technique for solving the flexural problems of clamped orthotropic rectangular shaped thin plates resting on one-parameter elastic foundations. In [39], the authors used the exact wave propagation approach for the natural vibration and stability analysis of thick plates modelled using the third order shear deformation plate theory. In [40], the authors presented the refined plate theory for the natural vibration analysis of nanoplates. In [41], the authors investigated vibrational behaviour of nonlinear rectangular plates modelled using the shear deformation plate theory. In [42], the authors presented a new technique for solving nonlinear vibrational problems of rectangular plates subjected to inplane compressive forces. In [43], the authors used the trigonometric shear deformation plate theory for the flexural analysis of moderately thick plates according to the shear deformation assumptions.

Other contributions to the knowledge of plates are found in such seminal papers as presented by authors in [44-51].

Other contributions to the theory of plates are found in references [52–60].

In [61], the authors used the GITM for obtaining closed-form mathematical expressions for the stability problems of rectangular Kirchhoff plates.

In [62], the authors applied the finite integral transformation method to solve the flexural problems of rectangular Kirchhoff plates made with orthogonally anisotropic materials. They considered plates with two adjacent free boundaries and the other boundaries fixed or on simple suppports (FFCC or FFSS) plates.

In [63], the authors used the two-dimensional finite integral transformaion method to determine the mathematical expressions that solve the flexural problems of Kirchhoff plates that are rectangular in plan shape. They considered and studied such plates that are supported at the corner points.

In [64], the authors used the finte integral transformation method to solve the natural vibration problems for transversely anisotropic thin plates with opposite sides that are prevented from rotational displacement and the other sides free of support.

In [65], the authors used the techniques of finite integral transformation for flexural problems involving plates made of transversely-anisotropic materials where the plates opposite boundaries are fixed while the rest of the edges are free.

In [66], the authors used the two-dimensional finite integral transformation method to determine the mathematical expressions for the flexural problems of rectangular shaped plates with moderate thickness resting on Winkler foundations. They used the Mindlin plate theory to describe the plate and obtained the solutions to the system of governing equaitons using the two-dimensional finite integral tansformation technique.

2. Theory

2.1. The thin plate flexure problem:

The governing PDE describing flexure for thin plates a ´ b which is displayed in Figure 1 is given by the PDE:

where Ñ⁴ is the biharmonic operator, q(x, y) represents distribution of applied load intensity, w(x, y) denotes the deflection. D denotes the flexural rigidity of the plate, expressed in terms of the elastic properties and geometrical properties of the plate by Equation (2) as follows:

m is Poisson’s ratio, h is plate thickness. E is Young’s modulus of elasticity.

For clamped edges, the restraint equations for displacements are:

For (x = 0, y) and (x = a, y) edges, restraint (displacement) and bending moment force equations give:

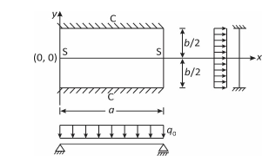Figure 1: Rectangular thin plate  with two opposite clamped boundaries  others on simple supports (SCSC or CSCS plate) subject to uniformly distributed transverse loading

2.2. Field equations for stability of rectangular thin plates subjected to uniaxial and biaxial compressive forces

The governing equation for the problem shown in Figure 2 is for biaxial buckling given by:

Figure 2: Biaxial buckling of rectangular thin (SCSC or CSCS) plates

The geometric and force equations for the buckling problem are expressed by Equations (3–6).

3. Methodology

In the Generalized Integral Transformation Method (GITM), the basis functions are chosen as the eigenfunctions of a freely vibrating thin beam of equivalent edge support conditions as the plate. The plate is simply supported along the boundaries x = 0, and x = a. The eigenfunction of a simply supported thin beam of span a at the nth vibration mode is:

n = 1, 2, 3, 4, 5, 6, …

The eigenfuction of a thin beam of span b clamped at y = ±b/2 at the mth vibration mode is given by:

m = 1, 2, 3, 4, 5, 6, …

In compact form,

where

where b_m are the roots (eigenvalues) of the eigen equation, which for clamped-clamped thin beams is a transcendental equation.

The roots (which are infinite in numbers) are obtained for the first five modes of vibration using Mathematica software as follows:

For large values of  and

Approximate solutions (eigenvalues) of the transcendental equation for m > 5 are obtained by solving the equation – Equation (18) using Mathematica and other root-finding software.

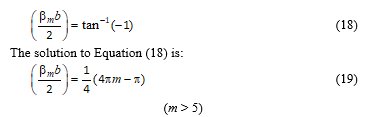Then, w(x, y) is constructed from the double infinite series of eigenfunctions in the x and y Cartesian coordinates as the following infinite double series:

where C_mn is an unknown displacement (deflection) parameter sought for w(x, y) to be a solution to the governing equation.

It is easily verified that F_1n(x) and F_2m(y) both satisfy all the boundary conditions of the thin plate problem for both flexure and elastic buckling.

3.1. The thin plate flexural problem

Applying the GITM to the PDE of the thin plate flexure problem results in the integral equation given as:

K_nm(x, y) denotes the nucleus (kernel) function.

Hence, simplification of Equation (21) gives:

where the primes represent differentiations with respect to the respective space coordinates.

For any m, n, we have C_mn determined by:

Then,

By differentiation,

The bending moments are:

At the plate centre, the bending moment expressions for M_xx and M_yy found by substitution of the centroidal coordinates are:

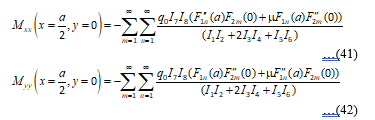At the middle of the clamped boundaries, the coordinates are:

The bending moment expressions for the midpoint of the fixed boundaries are found and given by:

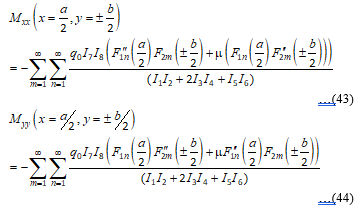3.2. Biaxial buckling of SCSC plate

The application of GITM to the elastic buckling equation gives the integral equation:

Then,

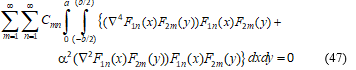Simplifying Equation (47) gives:

Hence,

3.3. Uniaxial buckling of SCSC plate

For uniaxial buckling due to N_x applied alone, N_y = 0, and the GITM yields:

The buckling load for uniaxial compression in the x direction is:

4. Results

By differentiation of the eigenfunctions,

Then,

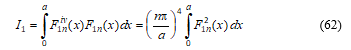Substitution of the expression for F_1n and integration gives:

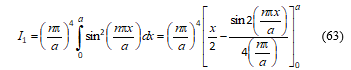Substituting the integration limits gives:

Similarly, I₂ is evaluated as:

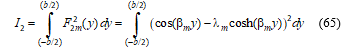Expanding the integrand in Equation (65) gives:

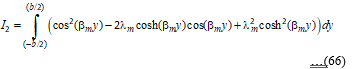Using the linearity property of integration, Equation (66) simplifies to:

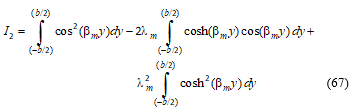Each integral in Equation (67) is evaluated.

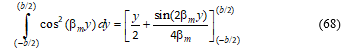Substituting the limits, and simplifying, gives:

Similarly,

Also,

Then, substitution of Equations (69) (72) and (74) into Equation (67) yields:

I₄ is evaluated as:

Similarly,

4.1.  Results for the thin plate flexure problem

Then, substituting the integrals into Equation (25), we have:

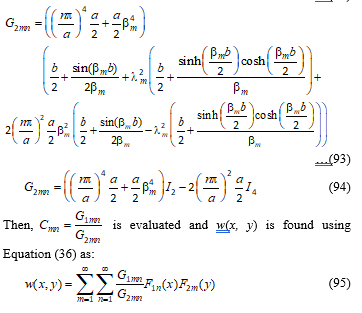where m = 1, 2, 3, …; n = 1, 2, 3, …

The bending moments are obtained from substitution of Equation (95) in Equations (7) and (8):

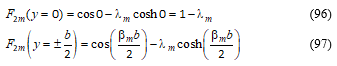
Results for deflections and bending moments evaluated at x = a, y = 0

The deflections and bending moments expressions evaluated at x = a, y = 0 are found from:

Results for deflection and bending moment expressions evaluated at the midpoint of the fixed edges  

The deflection and bending moments expressions evaluated at the midpoint of the fixed edges are found and given by:

The obtained results are presented in Tables 1, 2, 3, 4, 5, 6, 7, 8 and 9.

Table 1: Maximum deflection coefficients (a₁) of rectangular Kirchhoff CSCS plate having clamped boundaries  two opposite boundaries (x = 0, x = a), simply supported and the plates submitted to uniform load of intensity q₀ (case when b £ a or a ³ b) for

a/b
	Present study (GITM) a1	[1]  a1
1.0	1.92 ´ 10–3	1.92 ´ 10–3
1.1	2.09 ´ 10–3	2.09 ´ 10–3
1.2	2.23 ´ 10–3	2.23 ´ 10–3
1.3	2.34 ´ 10–3	2.34 ´ 10–3
1.4	2.40 ´ 10–3	2.40 ´ 10–3
1.5	2.47 ´ 10–3	2.47 ´ 10–3
2	2.60 ´ 10–3	2.60 ´ 10–3
¥	2.60 ´ 10–3	2.60 ´ 10–3

Table 2: Maximum deflection coefficient (a₂) of rectangular Kirchhoff CSCS plates with clamped boundaries  opposite simply supported boundaries (x = 0, x = a) where the plate carries uniform loading with an intensity q₀ (case when b ³ a) for

b/a
	Present study (GITM) a2	[1] a2
1.0	1.92 ´ 10–3	1.92 ´ 10–3
1.1	2.51 ´ 10–3	2.51 ´ 10–3
1.2	3.19 ´ 10–3	3.19 ´ 10–3
1.3	3.88 ´ 10–3	3.88 ´ 10–3
1.4	4.60 ´ 10–3	4.60 ´ 10–3
1.5	5.31 ´ 10–3	5.31 ´ 10–3
1.6	6.03 ´ 10–3	6.03 ´ 10–3
1.7	6.68 ´ 10–3	6.68 ´ 10–3
1.8	7.32 ´ 10–3	7.32 ´ 10–3
1.9	7.90 ´ 10–3	7.90 ´ 10–3
2	8.44 ´ 10–3	8.44 ´ 10–3
3	11.68 ´ 10–3	11.68 ´ 10–3
¥	13.02 ´ 10–3	13.02 ´ 10–3

Table 3:  convergence study of the maximum deflection function for CSCS (or SCSC) plate for the cases where b < a (or a > b) for

a/b	Present study n = 1, m = 1 a1	Relative error	Present study n = 1, 3, m = 1, 2 a1	Relative error	[1] a1
1.0					1.92 ´ 10–3
1.1	2.188125 ´ 10–3	4.69	2.081875 ´ 10–3	-0.39	2.09 ´ 10–3
1.2	2.345625 ´ 10–3	5.18	2.21625 ´ 10–3	-0.62	2.23 ´ 10–3
1.3	2.476875 ´ 10–3	5.85	2.320625 ´ 10–3	-0.83	2.34 ´ 10–3
1.4	2.585625 ´ 10–3	7.73	2.399375 ´ 10–3	-0.03	2.40 ´ 10–3
1.5	2.67625 ´ 10–3	8.35	2.461875 ´ 10–3	-0.45	2.47 ´ 10–3
2	2.64875 ´ 10–3	1.875	2.59375 ´ 10–3	-0.24	2.60 ´ 10–3
¥	2.63625 ´ 10–3	1.39	2.60125 ´ 10–3	-0.05	2.60 ´ 10–3

Table 4: Convergence study of the maximum deflection of the CSCS plate studied for the cases where b < a up to 5 terms each of the series for

a/b	n = 1, m = 1 a1 (´10–3)	n = 1, 3 m = 1, 2 a1 (´10–3)	n = 1, 3,  5 m = 1, 2, 3 a1 (´10–3)	n = 1, 3,  5, 7 m = 1, 2, 3, 4 a1 (´10–3)	n = 1, 3,  5, 7, 9 m = 1, 2, 3, 4, 5 a1 (´10–3)
1.1	2.188125	2.081875	2.09125	2.089375	2.09
1.2	2.345625	2.21625	2.228125	2.225625	2.23
1.3	2.476875	2.320625	2.335625	2.3325	2.34
1.4	2.585625	2.399375	2.418125	2.414375	2.40
1.5	2.67625	2.461875	2.481875	2.476875	2.47
2	2.64875	2.59375	2.623125	2.610625	2.60
¥	2.63625	2.60125	2.605	2.60375	2.60

Table 5: Convergence study of the maximum value of deflection of CSCS Kirchhoff plates studied for cases b ³ a for

b/a	a2 n = 1, m = 1 (´10–3)	a2 n = 1, 3 m = 1, 2 (´10–3)	a2 n = 1, 3,  5 m = 1, 2, 3 (´10–3)	a2 n = 1, 3,  5, 7 m = 1, 2, 3, 4 (´10–3)	a2 n = 1, 3,  5, 7, 9 m = 1, 2, 3, 4, 5 (´10–3)
1.0	1.998125	1.91125	1.919375	1.9175	1.92
1.1	2.625	2.520625	2.53	2.5275	2.509375
1.2	3.310625	3.184375	3.195625	3.193125	3.13375
1.3	4.035	3.8825	3.896875	3.89375	3.88
1.4	4.778125	4.594375	4.55	4.60875	4.60
1.5	5.5225	5.3025	5.3250	5.32	5.31
1.6	6.2875	5.9925	6.02	6.01375	6.03
1.7	6.960625	6.651875	6.685625	6.680625	6.68
1.8	7.635	7.27375	7.314375	7.305625	7.32
1.9	8.2725	7.8525	7.901875	7.89125	7.90
2	8.87	8.38625	8.445	8.4325	8.44
3	12.866875	11.50375	11.7325	11.67625	11.68
¥	13.07125	13.0175	13.02125	13.020625	13.02

Table 6: Bending moment coefficients evaluated at the centroidal coordinates of CSCS plates edges (x = 0, x = a) on simple supports, two sides  fixed with the plate carrying uniform loading of intensity q₀ (case where b < a, and m = 0.30)

a/b	Present study a3	[1] a3	Present study a4	[1] a4
1.1	0.0230	0.0230	0.0355	0.0355
1.2	0.0215	0.0215	0.0375	0.0375
1.3	0.0203	0.0203	0.0388	0.0388
1.4	0.0192	0.0192	0.0399	0.0399
1.5	0.0179	0.0179	0.0406	0.0406
2	0.0142	0.0142	0.0420	0.0420
¥	0.0125	0.0125	0.0417	0.0417

Table 7: Bending moment coefficients for uniformly loaded rectangular Kirchhoff CSCS plate studied. Sides  clamped, opposite edges (x = 0, x = a) on simple supports (case where b ³ a, and m = 0.30)

b/a
	a5 Present study (GITM)	[1] a5	a6 Present study (GITM)	[1] a6
1.0	0.0244	0.0244	0.0332	0.0332
1.1	0.0307	0.0307	0.0371	0.0371
1.2	0.0376	0.0376	0.0400	0.0400
1.3	0.0446	0.0446	0.0426	0.0426
1.4	0.0514	0.0514	0.0448	0.0448
1.5	0.0585	0.0585	0.0460	0.0460
1.6	0.065	0.0650	0.0469	0.0469
1.7	0.0712	0.0712	0.0475	0.0475
1.8	0.0768	0.0768	0.0477	0.0477
1.9	0.0821	0.0821	0.0476	0.0476
2	0.0869	0.0869	0.0474	0.0474
3	0.1144	0.1144	0.0419	0.0419
¥	0.0125	0.0125	0.0375	0.0375

Table 8: Bending moment coefficients at the midpoint of the fixed edges of rectangular Kirchhoff CSCS plate under uniform loading over the plate domain (for the case b < a) for

a/b
	a7 Present study (GITM)	[1] a7
1.1	-0.0739	-0.0739
1.2	-0.0771	-0.0771
1.3	-0.0794	-0.0794
1.4	-0.0810	-0.0810
1.5	-0.0822	-0.0822
2	-0.0842	-0.0842
¥	-0.0833	-0.0833

Table 9: Bending moment coefficients at the midpoint of fixed edges of thin CSCS plates carrying uniform loading (cases b ³ a; m = 0.30)

b/a
	a8 Present study (GITM)	[1] a8
1.0	-0.0697	-0.0697
1.1	-0.0787	-0.0787
1.2	-0.0868	-0.0868
1.3	-0.0938	-0.0938
1.4	-0.0998	-0.0998
1.5	-0.1049	-0.1049
1.6	-0.1090	-0.1090
1.7	-0.1122	-0.1122
1.8	-0.1152	-0.1152
1.9	-0.1174	-0.1174
2	-0.1191	-0.1191
3	-0.1246	-0.1246
¥	-0.1250	-0.1250

4.2. Results for stability problems studied

4.2.1.      Biaxial buckling of CSCS plate

G_2mn is found from Equation (93)

N is calculated from Equation (54).

For m = 1, n = 1, an approximate value for N for biaxial buckling load as well as the buckling load in uniaxial compression are found as follows:

Then,

Similarly, a one term solution for the buckling load for uniaxial compression in the x duration is given by:

The exact solution for the lowest/critical elastic buckling load in uniaxial compression in the x Cartesian coordinate direction is [1]:

The obtained GITM solution for the elastic buckling load under uniaxial uniform compression of CSCS plate for a one term approximation is 12.23% greater than the exact solution. It is suggested that more acceptable solutions that do not differ markedly from the exact solution for the elastic stability problems of square CSCS plates under uniaxial compressive loading could be obtained by using more terms in the eigenfunction expansion.

5. Discussion

The Generalized Integral Transform Method (GITM) has been used in this work to solve the bending and buckling problems of rectangular thin plates having two boundaries (x = 0, x = a) on simple supports and the other two boundaries (y = ±b/2) fixed. In the thin plate bending problem presented, the plate was submitted to a uniform distribution of loading. The PDE for homogeneous, isotropic plates is the inhomogeneous biharmonic equation expressed by Equation (2). The natural and force equations at the supported boundaries are expressed using the Equations (3 – 6). The study thus presented solutions to the domain Equation (2) using the GITM, where the solutions are required to satisfy Equations (3 – 6) along the boundaries.

The elastic buckling problem considered in the study is given for biaxial compressive forces by Equation (9) or Equation (10) when the biaxial compressive forces are equal for both the x and y directions (N_x = N_y). The domain PDE for uniaxial buckling in the x direction is given by Equation (11). The boundary conditions for buckling are given by Equations (3 – 6). The two-dimensional GITM which is a generalization of the integral transform methods uses the eigenfunctions of an equivalent vibrating thin beam for the respective Cartesian coordinates as the basis functions in the respective coordinate directions.

Thus the basis functions (eigenfunctions) for the problem considered are chosen as Equations (12) and (13). The unknown displacement w(x, y) is considered to be constructed from the basis functions as the double infinite series given by Equation (20). The unknown deflection w(x, y) is a function of C_mn, unknown displacement parameters which are sought such that w(x, y) satisfies the domain equation at all point in the solution space.

The basis functions F_1n(x) and F_2m(y) each satisfies the geometric and force equation at the supports for both bending and elastic buckling analysis. The GITM transforms the governing PDE for plate bending to the integral equation given by Equation (21) where the kernel function is expressed by Equation (22). The general solution of the integral equation is found for C_mn as Equation (25) which is expressible using integrals I₁, I₂, …, I₈. Thus w(x, y) is determined as Equation (36). With the aid of bending moments-displacement equations, the bending moments are obtained in general as Equations (39) and (40). The expressions for bending moments evaluated at the plate centre are obtained as Equations (41) and (42). The expressions for M_xx and M_yy bending moments at the mid-point of the fixed edges are found as Equations (43) and (44).

The generalized integral transformation of the governing equation for elastic buckling (biaxial case) gave the integral equation – Equation (45). Simplification of the formulation yielded the algebraic eigenvalue problem in Equation (49).

For nontrivial solutions (C_mn ¹ 0) C_mn would not vanish and the elastic stability equation was obtained as Equation (50). The solution of the equation gave a² from which N could be found as Equation (51). Specializations of the solution for biaxial buckling gave the solution for uniaxial buckling as Equation (55).

The general solutions obtained for both cases of bending and elastic buckling analysis are presented in terms of integrals. The integrals are evaluated in order to determine specific expressions for G_1mn, G_2mn, G_3mn, G_4mn, which are determined explicitly as Equations (90), (91), (109) and (110) respectively.

The deflection was thus found explicitly as the double series of infinite terms as Equation (95). The deflection of the plate centre is thus found as Equation (102). The maximum deflection presented in Tables 1 and 2 occurs at the centre and agrees with the symmetrical features of the plate problem. The bending moments M_xx, M_yy are found at the plate centre and the middle point of the fixed sides and presented in Tables 6, 7, 8 and 9. Tables 3, 4 and 5 which present convergence studies of the double series for maximum deflection at the plate centre confirm the series as rapidly convergent. Satisfactorily accurate results for maximum deflection are found with a small number of terms of the obtained double infinite series for the maximum deflection. The converged results obtained for deflections and bending moments were in excellent agreement with solutions presented using the superposition principle [1].

The eigenvalue problem of buckling yielded the approximate expression for a² for m = 1, n = 1 from which N would be found as Equation (122) for biaxial buckling cases. For square thin plates the biaxial buckling load was found as Equation (123). The approximate expression for a² for m = 1, n = 1 for uniaxial buckling under uniform compression was found as Equation (124). N was obtained as the expression in Equation (125).

6. Conclusion

In conclusion

(i)        The GITM assumes the unknown w(x, y) to be a double infinite series constructed as products of the eigenfuncions F_1n(x) and F_2m(y) of vibrating Euler-Bernoulli beams with equivalent end support conditions respectively in the Cartesian coordinates, and terms C_mn sought to be determined.

(ii)       In the present problem the GITM assumes w(x, y) as the double infinite series of the product of C_mn and F_1n(x) and F_2m(y). F_1n(x) is the eigenfunction of a vibrating Euler-Bernoulli beam with simply supported ends which correspond to the simply supported boundaries of the plate. F_2m(y) denotes eigenfunction of a vibrating Euler-Bernoulli beam with clamped ends (y = ±b/2) which corresponds to the clamped boundaries (y = ±b/2) of the thin plate being studied.

(iii)      The eigenfunctions F_1n(x) and F_2m(y) thus satisfy the geometric and force equations of the thin rectangular CSCS plates considered for the two cases of bending analysis and elastic buckling analysis considered in the study.

(iv)      The GITM uses the eigenfunctions F_1n(x) and F_2m(y) as the integral kernel functions in the formulation of the integral equation from the domain equation for both the bending analysis and the elastic buckling analysis presented.

(v)       The application of GITM to the governing domain PDE converts the PDE over the domain to an integral equation in both cases of bending and elastic buckling analysis.

(vi)      The integral equations further reduce to algebraic problems for bending analysis leading to the determination of the unknown displacement parameters C_mn, and the full determination of the deflection w(x, y).

(vii)     The integral equation reduces to an algebraic eigenvalue equation for elastic buckling analysis, leading to the determination of a² and thus N for nontrivial solutions.

(viii)    The bending moment expressions were found as double series with infinite terms.

(ix)      The expressions for the maximum values of the deflection and bending moments are found to be rapidly convergent double series of infinite terms in m, and n.

(x)       The maximum values for deflection and bending moments were found to occur at the plate centre, thus agreeing with the symmetrical features of the plate problems considered.

(xi)      Convergence studies done and presented in Tables 3, 4 and 5 for the deflection expression computed at the plate centre validate that the deflection expression is rapidly convergent series, and exact solutions are obtained using five terms of the series in x and y directions.

(xii)     Satisfactorily accurate results are obtained for the maximum deflection with just a small number of terms of the infinite series expression.

(xiii)    For the verification and validation of the plate bending results found using the GITM in this work, the numerical values of the maximum deflections and maximum bending moments obtained were compared with values obtained for the same problem solved using the superposition technique. Good agreement between the present GITM solutions and solutions by superposition presented by authors in [1] was observed.

(xiv)    The GITM gave closed form mathematical expression as analytical solutions to the plate bending problem studied.

(xv)     The eigenvalue problem of elastic buckling studied for biaxial loading in uniform compression was illustrated using the first terms from the eigenfunction, and the approximate value of the buckling load computed for square CSCS plates.

(xvi)    The approximated value of the elastic buckling load was also found for uniaxial uniform compression of square CSCS plate and the obtained result had a relative error of 12.23% compared with the exact solution. This demonstrates, the relative accuracy of the GITT since a 1 ´ 1 term approximation gave a relatively small error. The use of more terms would definitely yield better results for the buckling load; however, with huge computational efforts (even with software due to the large demands of computer memory size/space).

Conflict of Interest

The authors hereby affirm and declare that they have no conflict of interest whatsoever in the publication and dissemination of this research work.

Acknowledgment

The authors sincerely and heartily acknowledge the constructive contributions of the reviewers, and the hard work and sincere commitment of the Editor-in-Chief and the Editorial Board members. The authors are grateful for all the efforts leading to the acceptance of the paper for publication in the journal.

1. S. Timoshenko, S. Woinowsky-Krieger, Theory of Plates and Shells, Second Edition, McGraw Hill Book Company, 1987.
2. K. Chandrashekhara, Theory of Plates, Universities Press (India) Limited Hyderabad, 2001.
3. R.D. Mindlin, “Influence of rotary inertia on flexural motion of isotropic, elastic plates” Journal of Applied Mechanics, 18(1), 31–38, 1951.
4. N.N. Osadebe, C.C. Ike, H. Onah, C.U. Nwoji, F.O. Okafor, “Application of the Galerkin-Vlasov method to the flexural analysis of simply supported rectangular Kirchhoff plates under uniform loads” Nigerian Journal of Technology, 35(4), 732–738, October 2016.
5. C.C. Ike, C.U. Nwoji, I.O. Ofondu, “Variational formulation of Mindlin plate equation and solution for deflections of clamped Mindlin plates” International Journal for Research in Applied Sciences and Engineering Technology, 5(1), 340–353, January 2017.
6. C.C. Ike, “First principles derivation of differential equations of equilibrium of anisotropic thin plates on elastic foundations” Journal of Geotechnical and Transportation Engineering, 4(1), 10–16, 2018.
7. C.U. Nwoji, B.O. Mama, C.C. Ike, H.N. Onah, “Galerkin-Vlasov method for the flexural analysis of rectangular Kirchhoff plates with clamped and simply supported edges” IOSR Journal of Mechanical and Civil Engineering, 14(2), Version 1, 61 – 74, April 2017. Doi-10.9790/1684-1402016174
8. B.O. Mama, C.C. Ike, H.N. Onah, C.U. Nwoji, “Analysis of rectangular Kirchhoff plate on Winkler foundation using Fourier sine transform method” IOSR Journal of Mathematics, 13(1), Version VI, 58–66, Jan–Feb 2017. Doi:10.9790/5728-1301065866
9. C.U. Nwoji, B.O Mama, H.N. Onah, C.C. Ike, “Kantorovich-Vlasov method for simply supported plates under uniformly distributed loads” International Journal of Civil, Mechanical and Energy Science, 3(2), 69–77, March–April 2017. http://dx.doi.org/10.24001/ijcmes.3.2.1
10. B.O. Mama, C.U. Nwoji, C.C. Ike, H.N. Onah, “Analysis of simply supported rectangular Kirchhoff plates by the finite Fourier sine transform method” International Journal of Advanced Engineering Research and Science, 4(3), 285–291, March 2017.https:.dx.doi.org/10.22161/ijaers.4.3.44.
11. R. Szilard, Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods, John Wiley and Sons Inc., New York 1056pp, 2004.
12. C.C. Ike, “Equilibrium approach in the derivation of differential equations for homogeneous isotropic Mindlin plates” Nigerian Journal of Technology, 36(2), 346–350, April 2017. http://dx.doi.org/10.4314/nijt.v36i2.4
13. C.U Nwoji, H.N. Onah, B.O. Mama, C.C. Ike, “Theory of elasticity formulation of the Mindlin plate equations” International Journal of Engineering and Technology, 9(6), 4344–4352, 2017. DOI:10.21817/ijet/2017/v9i6/170906074
14. C.C. Ike, “Mathematical solutions for the flexural analysis of Mindlin’s first order shear deformable circular plates” Journal of Mathematical Models in Engineering (JVE MME), 14(2), 50–72, June 2018. https//doi.org/10.21595/mme.2018.19825
15. G.U. Nwoji, B.O. Mama, H.N. Onah, C.C. Ike, “Flexural analysis of simply supported rectangular Mindlin plates under bisinusoidal transverse load” ARPN Journal of Engineering and Applied Sciences, 13(15), 4480–4488, August 2018.
16. H.N. Onah, M.E. Onyia, B.O. Mama, C.U. Nwoji, C.C. Ike, “First principles derivation of displacement and stress functions for three-dimensional elastostatic problems, and application to the flexural analysis of thick circular plates” Journal of Computational Applied Mechanics, 51(1), 184–198, June 2020. DOI: 10.22059/JCAMECH:2020.295989.471.
17. C.C. Ike, “Variational formulation of the Mindlin plate on Winkler foundation problem” Electronic Journal of Geotechnical Engineering, 22(12), 4829–4846, 2017.
18. C.C. Ike, C.U. Nwoji, E.U. Ikwueze, I.O. Ofondu, “Bending analysis of simply supported rectangular Kirchhoff plates under linearly distributed transverse load” Explorematics Journal of Innovative Engineering and Technology, 1(1), 28–36, September 2017.
19. C.C. Ike, “Flexural analysis of rectangular Kirchhoff plate on Winkler foundation using Galerkin-Vlasov variational method” Mathematical Modelling of Engineering Problems, 5(2), 83–92, June 2018. https//doi.org/10.18280/mmep.050205.
20. B.O. Mama, H.N. Onah, C.C. Ike, N.N. Osadebe, “Solution of free vibration equation of simply supported Kirchhoff plate by Galerkin-Vlasov method” Nigerian Journal of Technology, 36(2), 361–365, April 2017. http://dx.doi.org/10.4314/nijt.v36i2.6.
21. C.U. Nwoji, H.N. Onah, B.O. Mama, C.C. Ike, “Ritz variational method for bending of rectangular Kirchhoff-Love plate under transverse hydrostatic load distribution” Mathematical Modelling of Engineering Problems, 5(1), 1–10, March 2018. https://doi.org/10.18280/mmep.050101.
22. C.C. Ike, “Systematic presentation of Ritz variational method for the flexural analysis of simply supported rectangular Kirchhoff-Love plates” Journal of Engineering Sciences, 5(2), D1–D5, 2018.
23. C.C. Ike, “Ritz variational method for the flexural analysis of rectangular Kirchhoff plate on Winkler foundation” Journal of Engineering Sciences, 6(1), pp D7–D15, 2018.
24. Y.M. Ghugal, A.S. Sayyad, “A static flexure of thick isotropic plate using trigonometric shear deformation theory” Journal of Solid Mechanics, 2(1), 79–90, 2010.
25. Y.M. Ghugal, P.D. Gajbhiye, “Bending analysis of thick isotropic plates by using 5th order shear deformation theory” Journal of Applied and Computational Mechanics, 2(2), 80–95, 2016.
26. C.C. Ike, “Flexural analysis of Kirchhoff plates on Winkler foundations using finite Fourier sine integral transform method” Mathematical Modelling of Engineering Problems, 4(4), 145–154, Dec 2017.
27. C.C. Ike, “Double Fourier cosine series method for the flexural analysis of Kirchhoff plates on Winkler foundations” Journal of Geotechnical and Transportation Engineering, 4(2), 30–38, 2018.
28. C.C. Ike, “Kantorovich – EulerLagrange – Galerkin’s method for bending analysis of thin plates” Nigerian Journal of Technology, 36(2), 351–360, April 2017. https://dx.doi.org/10.4314/nijt.v36i2.5
29. C.C. Ike, C.U. Nwoji, “Kantorovich method for the determination of eigenfrequencies of thin rectangular plates” Explorematics Journal of Innovative Engineering and Technology, 1(1), 20–27, September 2017.
30. H.N. Onah, B.O. Mama, C.C. Ike, C.U. Nwoji, “Kantorovich-Vlasov method for the flexural analysis of Kirchhoff plates with opposite edges clamped and simply supported (CSCS plates)” International Journal of Engineering and Technology, 9(6), 4333–4343, 2017. Doi:10.21817/ijet/2017/v9i6/170906073
31. C.C. Ike, B.O. Mama, “Kantorovich variational method for the flexural analysis of CSCS Kirchhoff-Love plates” Journal of Mathematical Models in Engineering (JVE – MME), 4(1), 29–41, 2018. https://doi.org/10.21595/mme.2018.19750.
32. C.U. Nwoji, H.N. Onah, B.O. Mama, C.C. Ike, E.U. Ikwueze, “Elastic buckling analysis of simply supported thin plates using the double finite Fourier sine integral transform method” Explorematics Journal of Innovative Engineering and Technology, 1(1), 37–47, September 2017.
33. H.N. Onah, C.U. Nwoji, C.C. Ike, B.O. Mama, “Elastic buckling analysis of uniaxially compressed CCSS Kirchhoff plate using single finite Fourier sine integral transform method” Modelling, Measurement and Control B, 87(2), 107–111, June 2018. doi:10.18280/mmc_b.87.0208.
34. M.E. Onyia, E.O. Rowland-Lato, C.C. Ike, “Galerkin-Kantorovich method for the elastic buckling analysis of thin rectangular SCSC plates” International Journal of Engineering Research and Technology, 13(4), 613–619, 2020.
35. M.E. Onyia, E.O. Rowland-Lato, C.C. Ike, “Galerkin-Vlasov variational method for the elastic buckling analysis of SSCF and SSSS rectangular plates” International Journal of Engineering Research and Technology, 13(6), 1137–1146, 2020.
36. M.E. Onyia, E.O. Rowland-Lato, C.C. Ike, “Elastic buckling analysis of SSCF and SSSS rectangular thin plates using the single finite Fourier sine integral transform method” International Journal of Engineering Research and Technology, 13(6), 1147–1158, 2020.
37. A. Ghannadiasi, A. Noorzad, “Bending solution for simply supported annular plates using the indirect Trefftz boundary method” Civil Engineering Infrastructures Journal, 49(1), 127–138, June 2016. DOI:10.7508/CEIJ.2016.01.009.
38. A.M.M. Bidgoli, A.R. Daneshmehr, R. Kolahchi, “Analytical bending solution of fully clamped orthotropic rectangular plates resting on elastic foundations by the finite integral transform method” Journal of Applied and Computational Mechanics, 1(2), 52–58, 2015. DOI:10.22055/JACM.2014.10742.
39. A. Zargaripoor, A. Bahrami, M. Nikkhah-Bahrami, “Free vibration and buckling analysis of third-order shear deformation plate theory using exact wave propagation approach” Journal of Computational Applied Mechanics, 49(1), 86–101, 2018. DOI:10.22059/JCAMECH.2018.248906.223.
40. M. Goodarzi, M. Nikkhah-Bahrami, V. Tavaf, “Refined plate theory for free vibration analysis of FG nanoplates using the nonlocal continuum plate model” Journal of Computational Applied Mechanics, 48(1), 123–136, 2017.DOI:10.22059/JCAMECH.2017.236217.155.
41. R. Javidi, M.M. Zand, K. Dastani, “Dynamics of nonlinear rectangular plates subjected to an orbiting mass based on shear deformation plate theory” Journal of Computational Applied Mechanics, 49(1), 27–36, 2018.DOI:10.22059/JCAMECH.2017.238716.169.
42. H. Makvandi, S. Moradi, D. Poorveis, K.H. Shirazi, “A new approach for nonlinear vibration analysis of thin and moderately thick rectangular plates under inplane compressive load” Journal of Computational Applied Mechanics, 48(2), 185–198, 2017. DOI:10.22059/JCAMECH.2017.240726.181.
43. A. Sayyad, Y.M. Ghugal, “Bending of shear deformable plates resting on Winkler foundations according to trigonometric plate theory” Journal of Applied and Computational Mechanics, 4(3), 187–201, 2018. DOI:10.22055/JACM.2017.23057.1148.
44. A. Mirzapour, M. Eskandari-Ghadi, A. Ardeshir-Behrestaghi, “Analysis of transversely isotropic half spaces under the effect of bending of a rigid circular plate” Civil Engineering Infrastructures Journal, 45(5), 601–610, 2012.
45. F. Shahabian, S.M. Elachachi, D. Breysse, “Safety analysis of the patch load resistance of plate girders: Influence of model error and variability” Civil Engineering Infrastructures Journal, 46(2), 145–160, 2003. DOI:10.7508/CEIJ.2013.02.003.
46. G. Abdollahzadeh, F. Ghobadi, “Mathematical modelling of column-base connections under monotonic loading” Civil Engineering Infrastructures Journal, 47(2), 255–272, 2014. DOI:10.7508/CEIJ.2014.02.008.
47. L. Cuba, R.A. Arciniega, J.L. Mantari, “Generalized 2-unknown’s HSDT to study isotropic and orthotropic composite plates” Journal of Applied and Computational Mechanics, 5(1), 141–149, 2019. DOI: 10.22055/JACM.2018.24953.1222.
48. A. Jahanpour, F. Roozbahani, “An applicable formula for elastic buckling of rectangular plates under biaxial and shear loads” Aerospace Science and Technology, 56, 100–111, 2016. http://dx.doi.org/10.1016/J.AST.2016.07.005.
49. J. Zhang, C. Zhou, S. Ullah, Y. Zhong and L. Rui, “Two-dimensional generalized finite integral transform method for new analytic bending solutions of orthotropic rectangular thin foundation plates” Applied Mathematics Letters, 92, 8–12, June 2019.
50. S. Ullah, J. Zhang, Y. Zhong, “Accurate buckling analysis of rectangular thin plates by double finite sine integral transform method” Structural Engineering and Mechanics, 72(4), 491–502, 2019. Doi:http://dx.doi.org//10.12989/sem.2019.72.4.491.
51. O.A. Oguaghamba, C.C. Ike, “Single finite Fourier sine integral transform method for the determination of natural frequencies of flexural vibration of Kirchhoff plates” International Journal of Engineering Research and Technology, 13(3), 470–476, 2020.
52. E. Ventsel, T. Krauthammer, Thin Plates and Shells, Marcel Dekker Inc. USA, 2001.
53. E.H. Mansfield, The Bending and Stretching of Plates, Cambridge University Press, Cambridge, 1989.
54. R. Vinson Jack, Solid Mechanics and its Applications – Plate and Panel Structures of Isotropic Sandwich Construction, Springer Dordrecht, Netherlands, 2005.
55. P.S. Chen, N.N. Archer, “Solutions of a twelfth order thick plate theory” Acta Mechanics, 79, 77–111, 1989.
56. C.C. Ike, C.U. Nwoji, B.O. Mama, H. N. Onah, M.E. Onyia. “Least squares weighted residual method for finding the elastic stress fields in rectangular plates under uniaxial parabolically distributed edge loads”. Journal of Computational Applied Mechanics 51(1), 107-121. Doi: 10.22059/JCAMECH.2020.298074.484.
57. D. Durban, D. Givoli, J.G. Simnonds (Eds), Solid Mechanics and its Applications Advances in the Mechanics of Plates Shells: The Avio nvan Libai Anniversary Volume Kluwer Academic Publisher Dordrecht, Netherlands, 2001
58. C.H. Aginam, C.A. Chidolue, C.A. Ezeagu, “Application of direct variational method in the analysis of isotropic thin rectangular plates” ARPN Journal of Engineering and Applied Sciences, 7(9), 1128–1138, September 2012.
59. J.N. Reddy, Energy Principles and Variational Methods in Applied Mechanics, John Wiley and Co Inc. New Jersey, USA, 2002.
60. A.C. Ugural, Stresses in Plates and Shells, McGraw Hill Book Co New York, 1999.
61. S. Ullah, Y. Zhong, J. Zhang, “Analytical buckling solutions of rectangular thin plates by straightforward generalized integral transform method” International Journal of Mechanical Sciences, 159, 535 – 544, 2019. DOI: 10.1016/j.ijmechsci.2019.01.025
62. Q. Xu, Z. Yang, S. Ulllah, Z. Jinghui, Y. Gao, “Analytical bending solutions of orthotropic rectangular thin plates with two adjacent edges free and the others clamped or simply supported using finite integral transform method” Advances in Civil Engineering, Vol 2020. Article ID: 8848879 (11pages), https://doi.org/10.1155/2020/8848879.
63. J. Zhang, C. Zhou, S. Ullah, Y. Zhong, R. Li, “Accurate bending analysis of rectangular thin plates with corner supports by a unified finite integral transform method” Acta Mechanica, 230(10), 3807 – 3821, 2019. DOI: 10.1007/s00707.019-02488-7
64. Y. Zhang, S. Zhang, “Free transverse vibration of rectangular orthotropic plates with two opposite edges rotationally restrained and remaining others free” Applied Sciences, 9(22): 1 – 13, 2019. doi.103390/app9010022
65. S. Zhang, L. Xu, “Analytical solutions for flexure of rectangular orthotropic plates with opposite rotationally restrained and free edges” Archives of Civil and Mechanical Engineering, 18(2018), 965 – 972, 2018. https://doi.org/10.1016/jacme.2018.02.005.
66. B. Tian, R. Li, Y. Zhong “Integral transform solutions to the bending problems of moderately thick rectangular plates with all edges free resting on elastic foundations” Applied Mathematical Modelling, 39(2015), 128 – 136, 2015.

(Click Here)

(Click Here)

No. of Downloads Per Month

No. of Downloads Per Country