1. Introduction

With the increase in multidimensional applications of internet based multimedia content, secure transmission of multimedia data including images has become the need of the day. Biometric image based security is deployed in all the electronic gadgets. Electronic transactions are involved in day today life. Various multimedia applications include transmission variety of images though the computer networks.  Image encryption algorithms vary in the way they are developed, the domain in which they encrypt and the inputs they accept. Since the algorithms need to satisfy a variety of constraints imposed by different applications, there is a need for adaptivity. Adaptive encryption algorithms meet the security standards without compromising the quality of the transmission. Self-adaptive encryption techniques improve the security of the encryption.  Bringing adaptivity at various stages of encryption algorithm is a promising field of current era.

As image security is an elementary requirement in variety of applications ranging from IoT to aerospace communication, variety of constraints are imposed on the encryption methods.

Researchers have developed various algorithms to meet the specifications of the application intended. Based on implementation, image encryption techniques can be classified into cover a wide range of classes including:

• Nature Inspired Encryption
• Parallel Encryption
• Transform Domain Encryption
• Partial / Selective Encryption
• Self-Adaptive Encryption, etc

Many hybrid algorithms are developed recently with a proper blend of these classes, considering the relative advantages of various classes. For the comparative study proposed, two different algorithms are considered. First one is based on nature inspired encryption and the second is a blend of transform domain and self-adaptive encryption.

Majority of the nature inspired encryption algorithms are based on genetic algorithms (GA). Efficient image encryption algorithms exploit the basic techniques of the GAs which simulate processes in natural systems necessary for evolution.

2. Literature Survey

Genetic algorithms initialize a random population and define fitness of population (p). These algorithms randomly choose parents from p. Crossover operation is carried out on these parents, resulting in the creation of new population (p+1). The new population is mutated and the fitness of population (p+1) is determined. The entire process is repeated until best individual is good enough. This concept can be effectively used in the accomplishment of confusion and diffusion of pixels required for encryption. Genetic Algorithms possess the following limitations:

• requires a greater number of iterations for optimum solution
• convergence is spread across many parameters [1].

To overcome these limitations, it is essential to find and to improve GA and to increase the speed of convergence.  Various methods have been proposed to improvise the efficiency of GA [2-7]. In [8], a Chaos Genetic Algorithm (CGA) is proposed that employs logistic map to create the initial population. Limitation of this technique is that it still cannot generate diverse content in mutation for some complex circumstances. Work taken up in [9] is a feature selection method based on chaos GA using two different chaotic maps to keep up and improve the capability in global searching.

Various approaches to achieve confusion and diffusion based on genetic operations are presented in [10-14]. They utilize the fitness function for key generation and generation of cipher image. The pixels are permuted with DNA (Deoxyribo nucleic acid) based combinations to improve the encryption quality.  A scheme for the security of medical images based on the features of genetic algorithms is discussed in [15]. Limitations of these algorithms are that few of the parameters are not tested for the cipher images. The algorithms are efficient but complex in nature. Work in [16] cryptanalyzes a DNA based color encryption technique. Also, there is a different approach using predicted key pair values to breach the security of these algorithms as demonstrated   in [17].

Since the DNA based techniques do not change the pixel values non-linearly, they are prone to known plaintext attack. If one plain image is compromised, the enciphered image can be easily reconstructed without the help of keys. Optical encryption techniques target parallel processing of the image with multiple degree of freedom.

The image pixels are multiplied with random phase masks in the process of Double Random Phase Encryption (DRPE) in spatial and frequency domain. Optical encryption is performed with the keys generated in the transform domain. Work presented in [18-25] describe encryption techniques based on various transforms including fractional Fourier transform (FrFT), Radial Hilbert transform (RHT), Discrete Cosine Transform (DCT) and Hartley transform (HT).  Optical encryption exploits several image parameters, including color, amplitude, phase, spatial frequency, polarization, etc., to arrive at a robust and secure encryption. Also, the complications can be regulated by proper selection of the number of rounds and the fractional order.

Fractional transforms play a vital role in image encryption. They exhibit many beneficial assets of general transforms, and have an additional independent component, its fraction. If this fraction equals to zero, the output image is a modulated version of the input image. When the fraction equals to one, fractional transform is equivalent to the original regular transform. With the fraction varying from zero to unity, different versions of the signals interpolating between modulated form and the regular transformed version can be generated. Thus, the free component serves as a key for encipherment.

The fractal compression technique is another promising method for image encryption. It is a lossy compression technique that suits for the images having high similarity at different parts. Natural and texture images are the best examples for this kind of images. A compression-encryption algorithm based on the fractal coding is discussed in [26]. Even though the compression ratio is high, the algorithm suffers at the quality of encryption. Balancing the compression ratio and the encryption quality is an interesting topic for current research.

Fractional Fourier transform has found effective in image encryption and noise removal. A multiple parameter FrFT based scheme is discussed in [27], in which, the order is considered as a vector. This scheme provides flexibility for the dimension of transform order and improvises the strength of encrypted image while retaining low computational complexity and hardware cost. Fractional Fourier transform with vector power multi-parameters is another general form of the FrFT which has great significance in information processing security. Performance of various transform based techniques is compared in [28]. Even though it claims that chaos based encryption with discrete wavelet transform gives better performance, the NPCR (number of changing pixel rate) and UACI values need to be improved. A properly designed scrambler can improve these parameters.

Remote sensing (RS) is a booming technology that provides the dynamic information of the earth surface remotely and without contact. Remote sensing technology has been developed with an exponential rate due the improved research on the computers and graphic and playing a vital role in the national, economic, construction and defense related issues [29].

Latest studies of primary focus are on the protection of digital contents communicated using RS technology. Satellite remote sensing utilizes image distribution and characteristics with various structures of remote sensing image [30]. Recently purposeful hack assaults have demonstrated that interruption into satellite information is not an unimaginable assignment. A group at the Embry Riddle Aeronautical University figured out how to get National Oceanic and Atmospheric Administration (NOAA) satellite symbolism with fundamental contraption worked as a component of an exploratory venture and by utilizing open sources accessible from the Internet [31].

Cryptanayzers have been successful in breaking few of these algorithms with known/chosen plaintext cryptanalysis. The reason is that the same set of encryption keys are used to encipher different input plain images. Unfortunately, all these cryptosystems use the same key for quite a long period. The key set can be easily compromised by encrypting some distinct images like a completely white image or completely black image, and then associating the result with the equivalent enciphered output. In order to make the algorithms robust against the kind of attacks, a plaintext-related diffusion and confusion needs to be incorporated.  The key stream rudiments can be selected under the control of plain pixel. Secret keys must be associated not only to the control parameters but also to the parameters related to plain image, in order to make the known/chosen plaintext attack harder to succeed.

Self-adaptive encryption is considered as a method that has the encryption considering input image details. The dependency on the plain image content is strongly desirable characteristics of a good encryption algorithm since two images differing with few pixels will get encrypted into totally dissimilar patterns. The proposed technique generates the encryption keys dependent on the plain image features. Also, the technique arrives at a second level of self adaptivity since one part of the image gets encrypted by the influence of the other part.

Optical systems deploy transform based algorithms, which include, Fourier transform (FT), the fractional Fourier transform (FrFT), radial Hilbert transform (RHT). To add to these, there are also discrete fractional Fourier transform (DfrFT), discrete fractional cosine transform (DFrCT), and discrete fractional Sine transform (DFrST). Haar wavelet transform de-correlates the image pixels by decomposing into averaging and differencing components [32].The Hilbert transform exhibits edge enhancing properties and hence finds its use in processing of images and phase observation [33]. Radial Hilbert transform can increases the strength with expanded key space [34].

Satellite images are widely used in various applications including remote sensing, weather forecasting and vegetation based analysis, mineral/rock differentiation, plant species identification, forest classification, coastal water analysis, soil/vegetation differentiation, etc. [35]. Satellite images can be classified as infrared images, water vapor and visible images. Some features of the satellite images are high correlation among the pixels, bulkiness and large size. Since most of them are confidential, the traditional encryption methods lack in efficiency for bulky images and have a poor speed. To encrypt bulky images, a secure and high speed encryption algorithm is necessary.

The paper compares the performance of chaos based bio-inspired image encryption [36] and chaos based self-adaptive encryption using radial Hilbert transform [37].  The test is performed with three sets of images, namely, satellite images, face images and signature images as input data. Self-adaptive technique divides the plain image into sub-images and adds chaos. The encrypted image after jumbling yields an unsystematic, disordered image [38]. In the second method, image encryption is accomplished using multi-point crossover and mutation serving as bio-operational tools for confusion and diffusion.

3. Description of proposed techniques

3.1. Chaos Based Self Adaptive Encryption Using Radial Hilbert Transform (Technique 1)

Proposed technique employs Radial Hilbert transform. Hilbert Transform in fractional domain has been explored by Lohmann et al. [39]. Hilbert Transform has a special feature that it selectively emphasizes the features of the given input image during the spatial filtering process. Generally Hilbert Transform applied to an image builds its edge-enhanced version. In support to this, the fractional HT modifies the nature of the edge enhancement. A Hilbert filter yields an edge-enhanced image in a single dimension. 2D edge enhancement for the image can be accomplished by merging the response of two Hilbert filters orthogonal to each other. Still, these transformed images preserve the basic symmetry in rows and columns. A uniformly edge-enhanced image is the result of its radial version of the Hilbert transform. Since the Hilbert transform is helpful in enhancing the edges of one the input image, it is commonly used in image processing and phase observation. Three dimensional radially symmetrical Hilbert transform is mathematically represented as

H(a, b, 3) = exp(i * x * θ(a, b, 3))                     (1)

where x is a user defined parameter.

Self-adaptive encryption employs the keys generated form one part of the image to encrypt the other part. Proposed algorithm has the following components.

3.1.1. Image Encryption

Flow diagram of algorithm is as shown in Fig.1.Plane images are initially re-sized to MxN and divided into 4 sub-images with size (M/2, N/2).  It is divided into four sub-images (I₁, I₂, I₃ and I₄). First sub-image I₁ is encrypted using three input parameters: radial Hilbert transform, random chaos mask and a key x selected by the user. The Second sub-image I₂ is encrypted with a key calculated as the fraction of mean to standard deviation the previous sub-image I₁. This value also functions as an input to the radial Hilbert transform. Remaining sub-images are encrypted similarly. The encrypted sub-images are joined together and pixel positions are jumbled using a randomly generated matrix to get the final encrypted image. For decipherment, conjugate of the radial Hilbert transform and two random chaos masks are considered.

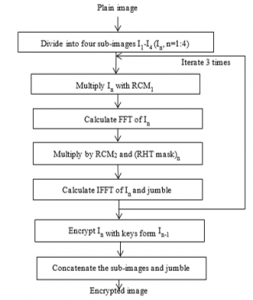
Figure 1: Radial Hilbert transform based image encryption process

3.1.2 Creation of Random Chaos Mask (RCM)

Two random three dimensional matrices having dimensions equal to that of the plain image ‘i’ are considered. These are considered as A₁ and A_2. Two random matrices are generated as

Ø₁ (a, b, 3) = exp(i * θ₁ (a, b, 3))                       (2)

Ø₂ (a, b, 3) = exp(i * θ₂ (a, b, 3))                       (3)

where  is the random chaos mask generated,  is the Fourier transform of randomly generated matrix.  These values are utilized in the generation of chaotic images A1 and A2 using logistic map which serve as a random chaos masks. The process is depicted in Figure 2.

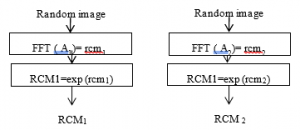
Figure 2: Generation of random phase mask (RCM)

3.1.3 Transformation with Radial Hilbert Transform

Each of sub-images undergoes a transformation as per equation (4), where x is a user defined value for sub- image I₁. For I₂-I₄, x is fraction of mean and standard deviation of previous sub-images.  θ(a,b,3) is the imaginary part of the Fourier transform for the sub- image I_n and H(a,b,3) is the Hilbert transform for sub- image I_n. By introducing radially symmetrical Hilbert transform, we can use it in three dimensions. The equation for radial Hilbert transform is given by

H (m, n, 3) = exp (i * x * θ (m, n, 3))                              (4)

The conjugate of radial Hilbert transform parameter is expressed as

H₁ (a, b, 3) = exp (-i * x * θ (a, b, 3))                               (5)

3.1.4 Results

The algorithm is applied on color images downloaded from Bhuvan, a Geo-portal of ISRO [40]. The images published on Bhuvan in 2D/3D domain are captured using many sensors and inform about the water, soil and land.

Figure 3: Input image for encryption

Figure 4: Sub-image I₁

Figure 5: Sub-image I₂

Figure 6: Sub-image I_3,

Figure 7: Sub-image I₄

Figure 8: First encrypted block

Figure 9: Second encrypted sub-block

Figure 10: Third encrypted sub-block

Figure 11: Fourth encrypted sub-block

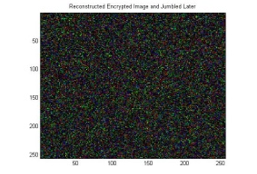
Figure 12: Complete encrypted image

Input satellite image shown in Figure 3 is divided into four smaller sub-images as displayed in Figure 4 -7. Each block is encrypted by the keys generated using the previous sub-image. The process is iterated three times for the entire image. Encrypted sub-images are displayed in Figure 8-11. Complete encrypted image is presented in Figure 12.

3.1.4.1 Histogram Analysis

Histogram analysis provides an overview of strength of confusion and diffusion for an image encryption algorithm, in presence of statistical attack. Histogram of plain image is obtained as shown in figure 13 (a) – (c). Histogram of encrypted image is shown by figure 14 (a) – (c). Histogram of the encrypted image gets exponentially distributed due to radial Hilbert transform.

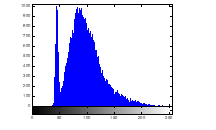
Figure 13(a): Histogram of plain image red channel

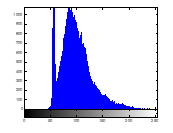
Figure 13(b): Histogram of plain image green channel

Figure 13(c): Histogram of plain image blue Channel

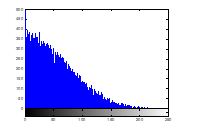
Figure 14(a): Histogram of encrypted image red channel

Figure 14 (b) Histogram of encrypted image green channel

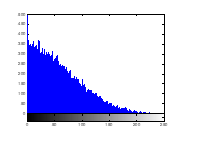
Figure 14(c): Histogram of encrypted image blue channel

3.1.4.2 Correlation of Two adjacent pixels

Correlation coefficients r(x,y) in horizontal, vertical  and diagonal directions are calculated with the equation 6.

where x and y are values of two neighboring pixels in the image, D(x) equals to the variance of x and COV(x, y) indicates the covariance of  x and  y.

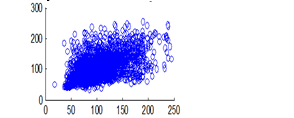
Figure 15(a): Horizontal pixel distribution of plain image for red plane

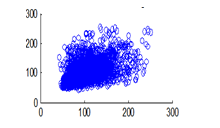
Figure 15(b): Horizontal pixel distribution of plain image for green plane

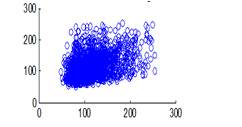
Figure 15(c): Horizontal pixel distribution of plain image for blue plane

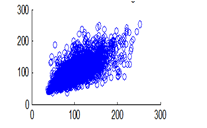
Figure 16(a): Vertical pixel distribution of plain image for red plane

Figure 16(b): Vertical pixel distribution of plain image for green plane

Figure 16(c): Vertical pixel distribution of plain image for blue pixel

Figure 16(a): Diagonal pixel distribution of plain image for red plane

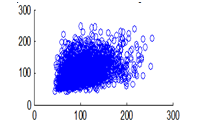
Figure 16(b): Diagonal pixel distribution of plain image for green plane

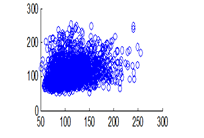
Figure 16(c): Diagonal pixel distribution of plain image for blue pixel

The experiment was conducted with 4096 pairs of neighboring pixels selected arbitrarily from the plain image and the enciphered image. Pixel distribution in Horizontal, Vertical and Diagonal directions corresponding to plain satellite image and encrypted image are plotted in figures 14 (a) –(c), 15 (a) – (c), 16 (a) –(c) and 17 (a) – (c), 18 (a) – (c), 19 (a) – (c) respectively. Encrypted image exhibits a uniform pixel distribution, which is a desirable property of a good encrypting algorithm to resist the statistical attacks. Correlation coefficients are given in table 1.

 

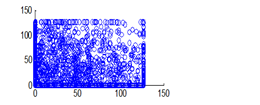
Figure 17(a): Horizontal pixel distribution of encrypted image for red plane

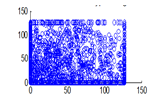
Figure 17(b): Horizontal pixel distribution of encrypted image for green plane

Figure 17(c): Horizontal pixel distribution of encrypted image for blue plane

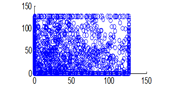
Figure 18(a): Vertical pixel distribution of encrypted image for red plane

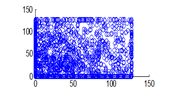
Figure 18(b): Vertical pixel distribution of encrypted image for green plane

Figure 18(c): Vertical pixel distribution of encrypted image for blue plane

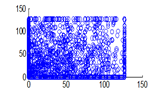
Figure 19(a): Diagonal pixel distribution of encrypted image for red plane

Figure 19(b): Diagonal pixel distribution of encrypted image for green plane

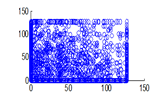
Figure 19(c): Diagonal pixel distribution of encrypted image for blue plane

Table 1: Correlation coefficients of two adjacent pixels in plain and encoded image

	Plain Image			Cipher Image
Color	R	G	B	R	G	B
HC	0.6316	0.5629	0.5239	0.0057	-0.0013	0.0027
VC	0.7814	0.7525	0.7312	-0.0072	0.0393	-0.0021
DC	0.5247	0.5058	0.4179	-0.0056	-0.0189	-0.0170

3.1.4.3 Sensitivity Analysis

Since this algorithm encrypts one sub-image 3 times it is less prone to differential attacks. The initial key is obtained from the user and a special operation on the initially encrypted image acts as the input for the next part of the original image using radial Hilbert transform. This makes the algorithm more powerful as the complete image cannot be decrypted at once with a single key. Four unique keys are required to decrypt the complete image. Input to radial Hilbert transform is image dependent. If the input given to radial Hilbert transform while decrypting is changed slightly, it leads to error propagation to the complete sub-image. The whole encrypted image changes as the sub images are interdependent. Thus the sensitivity is four times more than the algorithm with single key for the whole image. Figure 20 shows the deciphered image with a wrong key.

Figure 20: Deciphered image with a wrong key

To resist brute force attack, the algorithm must possess a very large key space. The technique proposed exhibits key sensitivity up-to 24 bits after the decimal point (10²⁴) and before the decimal point. There can be a range of 10²¹²⁸ combinations of keys.

3.1.4.4 Differential analysis

The number of changing pixel rate is to be analyzed to decide the robustness in case of differential attacks. It is a measure to decide how many pixels in the cipher-image change as one pixel in the plain image is changed. The NPCR value obtained equals to 99.99%. UACI value is equal to 32.6%. The results for the satellite image shown in figure 3 are given in table 2 which demonstrates the resistance to differential attacks.

3.1.4.5 Entropy Analysis

Information entropy of an image is a basic parameter to measure the randomness of pixels. A value of entropy near to 8 implies a random distribution.

Table 2: NPCR, UACI and entropy results

	Encrypted Image
Color	R	G	B
NPCR (%)	99.6368	99.6017	99.6201
UACI (%)	33.5262	33.6828	33.5840
Entropy (bits)	7. 7499	7. 4897	7.3896

3.2.  Nature Inspired Technique (Technique 2)

The general block diagram of the proposed encryption algorithm is shown in figure 21. The process includes a quantification unit, a logistic map generator, a mutation block, a crossover block and a scrambler. Chaotic sequence generator generates four chaotic sequences. The quantifier transforms these chaotic sequences into four streams of keys applied to crossover and mutation operations.  Crossover unit alters the order of the image pixels along the horizontal and vertical direction (confusion). The mutation unit disguises the encryption image with a random mask image (diffusion). The scrambler alters the position of the image pixels using a random sequence. Functionality of the various units is described as follows:

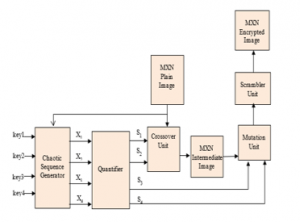
Figure 21: Architecture of the nature inspired image encryption algorithm

3.2.1 Chaotic Sequence Generator

Chaotic generator unit produces four random sequences with logistic map depending on the control parameters (µ1, µ2, µ3, µ4) and initial seed values (X₁₀, X₂₀, X₃₀, X₄₀). These keys form the set of shared secret values used in the cryptosystem. All the plain image pixels are added up and divided by (MxNx255). This fractional value is scaled down to 10% and added with the initial parameters. Thus the chaotic sequences generated are dependent on initial keys as well as the plain image. This makes the encryption algorithm stronger as the values X₁, X₂, X₃ and X₄ are not same with any two different images.  Logistic map is used for the generation of chaotic sequences.

3.2.2 Quantifier

The quantifier receives four chaotic arrays X₁– X₄ produced by the chaotic map and reforms them to four sequences S₁– S₄. The length of the 1^st and 3^rd key streams is chosen equal to M, and the length of the 2^nd and 4^th key streams is made equal to N, where M × N is the dimension of the plain image.

3.2.3 Crossover Unit

Let K_i and K_i+1 denote two sequential elements present in the key stream. Rows/columns numbered Ki and K_i+1 are undergo crossover process. Cut points occupy the positions in accordance with the following equation:

r₁ = max{1, | K_i  – K_{j _}+ 1|modL}                    (7)

r₂ = max {1, r₁ + | K_i  – K_{j _}+ 1|modL}           (8)

r_k = max {1, r_k-1 + | K_M  – K_N + 1|modL}       (9)

 

where k refers to the number of cut points, L = M or N = the length of the row/column, and (r₁,  r₂, …,  r_K) are the localities of cut points. Crossover operation at multiple points is executed by exchanging the even or odd numbered sectors of i and j.

3.2.4 Mutation Unit

Mutation unit disguises the transitional values rearranged after crossover by XORing with a random image. The random mask image is generated before the encryption process starts and shared between the two end users. Mutation unit changes each and every pixel in the intermediary image by XORing with an arbitrary pixel selected by the values of the S₃ and S₄ from the secrete mask image. Any (i, j)^th pixel in the enciphered image is attained by XORing the corresponding pixel in the transitional image and (p_i, q_j)^th pixel of the enciphered image, where p_i є S₃ and q_i є S₄.

3.2.5 Scrambler Unit

The scrambling is incorporated by altering the positions of the mutated image pixel values as per the elements in a random sequence generated by a random seed. The process for a sample sequence {2, 3, 1… N} is tabulated in table 3.

Table. 3: Scrambler unit design

	Random Sequence
Random Sequence		2	3	1	…	N
	2	(2,2)	(2,3)	(2,1)	…	(2,N)
	3	.	.	.	.	.
	.	.	.	.	.	.
	..	.	.	.	.	.
	N	(N,2)	(N,3)	(N,1)	..	(N, N)

3.2.6 Experimental results

A sample satellite image shown in Figure 22 is enciphered using the proposed method. Key used is {3.7158, 0.11, 3.89858, 0.25, 3.76158, 0.35, 3.8458, 0.6520}.  Figure 23 shows the encrypted image.

Figure 22: Original image,

Figure 23: Encrypted Image

3.2.6.1 Histogram Analysis

Figure 24(a): Histogram of plain image for red plane

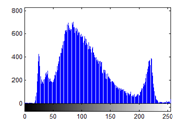
Figure 24(b): Histogram of plain image for green plane

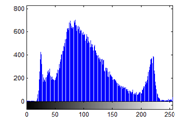
Figure 24(c): Histogram of plain image for blue plane

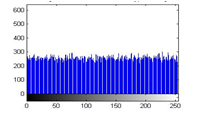
Figure 25(a): Histogram of cipher image for red plane

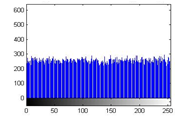
Figure 25(b): Histogram of cipher image for green plane

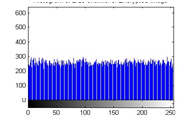
Figure 25 (c): Histogram of cipher image for blue plane

The histograms of plain image are presented in figure 24 (a)-(c). From figure 25(a)-(c), it is witnessed that the histogram of the encrypted image differs completely from the histogram of the plain image and has a uniform distribution, which is the desired property to make the algorithm hard for cryptanalysis.

3.2.6.2 Correlation Analysis

Correlation between two contiguous pixels corresponding to the plain image and cipher image is tested in this experiment. Horizontal, Vertical and Diagonal pixel distribution of plain image and cipher image for red, green and blue planes is shown in figures 26 (a) –(c), 27(a) –(c), 28(a)-(c) and 39(a)-(c), 40(a) –(c), 41(a)-(c) respectively. It is observed that the distribution is almost same and uniformly distributed for all the three-color planes in the cipher image.

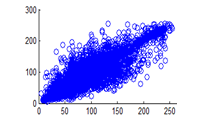
Figure 26(a):  Horizontal pixel distribution of plain image for red plane

Figure 26(b):  Horizontal pixel distribution of plain image for green plane

Figure 26(c):  Horizontal pixel distribution of plain image for blue plane

Figure 27(a): Vertical pixel distribution of plain image for red plane

Figure 27(b):  Vertical pixel distribution of plain image for green plane

Figure 28(c): Vertical pixel distribution of plain image for blue plane

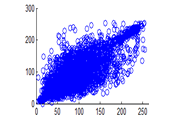
Figure 29(a): Diagonal pixel distribution of plain image for red plane

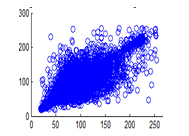
Figure 29(b): Diagonal pixel distribution of plain image for green plane

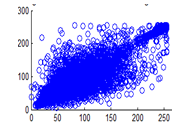
Figure 29(c): Diagonal pixel distribution of plain image for blue plane

Figure 30(a):  Horizontal pixel distribution of cipher image for red plane

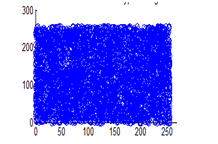
Figure 30(b):  Horizontal pixel distribution of cipher image for green plane

Figure 30(c):  Horizontal pixel distribution of cipher image for blue plane

Figure 31(a):  Vertical pixel distribution of cipher image for red plane

Figure 31(b):  Vertical pixel distribution of cipher image for green plane

Figure 31(c):  Vertical pixel distribution of cipher image for blue plane

Figure 32(a):  Diagonal pixel distribution of cipher image for red plane

Figure 32(b)  Diagonal pixel distribution of cipher image for green plane

Figure 32(c):  Diagonal pixel distribution of cipher image for blue plane

The following equations are used to obtain the correlation coefficients r(x,y) in horizontal (HC), vertical (VC) and diagonal (DC) directions:

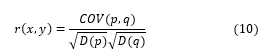
where p and q represent gray scale values of two neighboring pixels in the image, D(p) denotes the variance of p and COV (p, q) indicates the covariance of p and q.

The experiment was executed by selecting 4096 random adjacent pixel sets from the plain image and the ciphered image. Correlation coefficients are calculated using equation 3.3 and documented in table 4. It can be observed that the cipher image correlation coefficients are uniformly distributed in the range of 0-255 for all the three planes. This shows the strength of the algorithm towards statistical attacks.

Table 4: Correlation coefficients of two neighboring pixels in input and enciphered image

	Plain Image			Cipher Image
Color	R	G	B	R	G	B
HC	0.9545	0.9491	0.9223	-0.0005	-0.0008	0.0185
VC	0.9680	0.9558	0.9542	-0.0006	-0.0266	0.0052
DC	0.9269	0.9034	0.8875	-0.0242	-0.0109	-0.0051

3.2.6.3 Differential Analysis

The number of changing pixel rate and the unified averaged changed intensity are effective parameters used in the assessment of the robustness of an image encryption algorithm against differential attacks. Parameter NPCR implies the number of pixels changed over the encrypted image with only one single pixel in the plain image being varied. The UACI index represents difference in the intensity between plain and encrypted images on an average. The equations 1.9 and 1.10 are used in the calculation of NPCR and UACI respectively. The results for input satellite image shown in figure 3.5(a) are given in table 5 that shows the resistance at differential attacks

Table 5: NPCR, UACI and entropy results

	Encrypted Image
Color	R	G	B
NPCR (%)	99.6368	99.6017	99.6201
UACI (%)	33.5262	33.6828	33.5840
Entropy (bits)	7.9974	7.9974	7.9973

4. Comparative Study

A huge variety of chaos based image encryption algorithms have been modeled and developed in the past few years. Usually these algorithms are tested on a single image and the conclusion is drawn based on the performance parameters obtained. There arises a need to test the algorithms for a set of images with identical features and decide about the suitability of the algorithms for the input dataset. Proposed work attempts to analyze the results obtained with the algorithms tested using three datasets, namely, satellite images, face images and handwritten signature images. Sample images from each of these datasets are shown in Figure 33, 34 and 35.

 

Figure 33: Satellite image

Figure 34: Face image

Figure 35: Signature Image

The three datasets have a vast variation in their features. Satellite images have many small segments which show a high level of pixel variations. Also, the content is massive. Face images have few different segments with identical colors. Content is almost uniform in a segment.  Signature images have only two colors, blue and white. Pixels are almost identical except the blue colored area. Fifty images belonging to each class are considered in the comparative study.

4.1. Statistical features

Statistical parameters for the three sample images are provided in table 2. Satellite images have almost equal variation in the three planes, with an average centered at the middle value in the range of 0-255. Face images have a bit higher deviation in the three planes and the average is smaller as compared to satellite images. Signature images are centered at near white pixel because of the large white background. Variation is quite different for the three planes. However, all the three sets follow an identical pattern with respect to the correlation coefficients.

Table 5: Statistical parameters for the three datasets

Parameter	Satellite image	Face image	Signature image
mean	102.0983	85.4429	212.9507
standard deviation (R plane)	45.7829	53.3737	91.6546
standard deviation (G plane)	40.5145	44.4940	95.4395
standard deviation (B plane)	50.0683	52.0977	10.6353
correlation coefficient (R plane)	1	1	1
correlation coefficient (G plane)	0.8618	0.9209	0.9999
correlation coefficient (B plane)	0.9715	0.9480	0.3898
Entropy	7.303112	7.307502	2.740406

Results obtained with fifty images from each dataset are compared in the following section to decide about the suitability of the algorithm for the particular dataset. Performance parameters considered for the analysis include horizontal correlation, vertical correlation, diagonal correlation, net changing pixel rate, unified average change in intensity, entropy and encryption time taken by the encryption technique.

4.2. Results for Satellite Images

Fifty satellite images are considered for testing. They are RGB images with sizes varying from 128×128 to 1024×1024 pixels. The images are resized to 256×256 to bring the uniformity in the result. Performance parameters included in the analysis are correlation coefficient, NPCR, UACI, entropy and time required for encryption. Figure 36 (a) to (f) shows the plot of the pixel correlations for fifty encrypted satellite images.

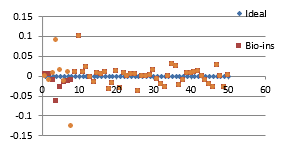
Figure 36(a): Horizontal correlation for 50 images

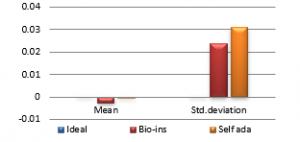
Figure 36(b): Mean Horizontal Correlation

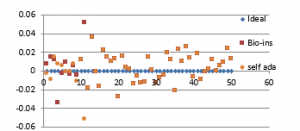
Figure 36 (c): Vertical Correlation for fifty images

Figure 36 (d): Mean vertical correlation

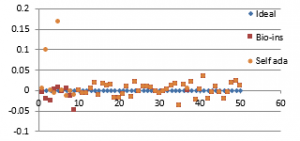
Figure 36(e): Diagonal Correlation for fifty images

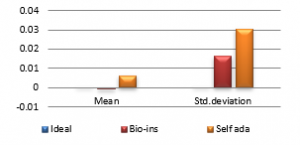
Figure 36(f): Mean Diagonal Correlation

Results of performance comparison for satellite images are displayed in Figure 37.

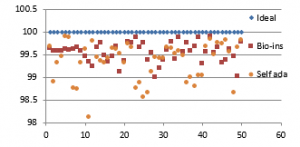
Figure 37(a): NPCR for fifty images

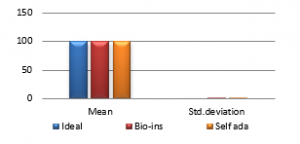
Figure 37 (b): Mean NPCR

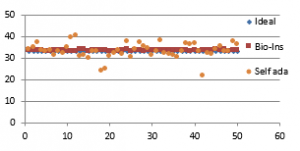
Figure 37(c): UACI for fifty images

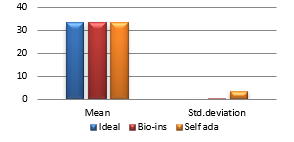
Figure 37(d): Mean UACI

Figure 37(e): Entropy for fifty images

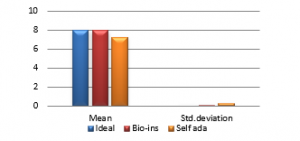
Figure 37(f): Mean Entropy

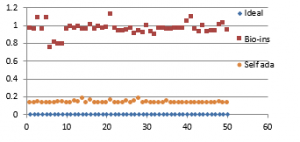
Figure 37(g): Encryption time for fifty images

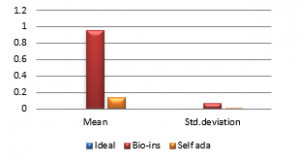
Figure 37(h): Mean encryption time

Referring to these results, Bio-inspired technique performs well with respect correlation coefficients, but requires more time for encryption. Self-adaptive method works well except entropy. Since the satellite images are generally bulky in size and sometimes need to be transmitted in real time, encryption time is also an important parameter to decide the capability of an algorithm. Self-adaptive encryption technique seems to be more time-efficient for the encryption of the satellite images.

4.3. Results for Face Images

Fifty RGB color images containing human face are provided as the inputs for testing. These images are obtained from an open source database [41] and have size of 180×200 pixels. Figure 38(a) to (f) displays the correlation parameters obtained for the fifty encrypted face images.

Figure 38(a): Horizontal Correlation for fifty images

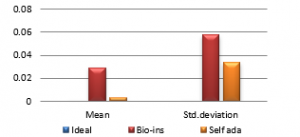
Figure 38(b): Mean Horizontal Correlation

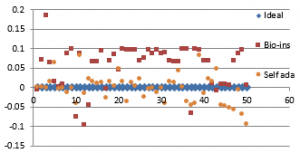
Figure 38(c): Vertical Correlation for fifty images

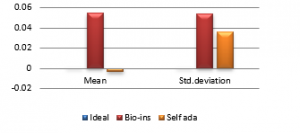
Figure 38(d): Mean Vertical correlation

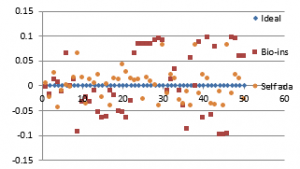
Figure 38(e): Diagonal correlation for fifty images

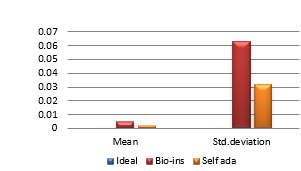
Figure 38(f): Mean Diagonal Correlation

Performance comparison for face images is visualized in Figure 39.

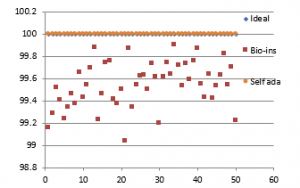
Figure 39 (a): NPCR for fifty images

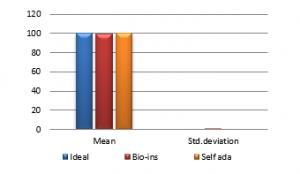
Figure 39(b): Mean NPCR

Figure 39(c): UACI for fifty images

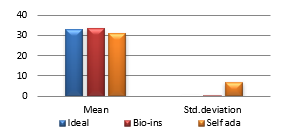
Figure 39(d): Mean UACI

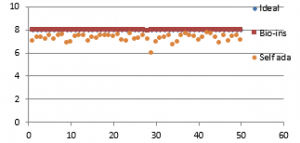
Figure 39(e): Entropy for fifty images

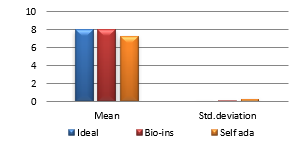
Figure 39(f): Mean Entropy

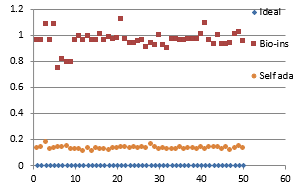
Figure 39(g): Encryption time for fifty images

Figure 39(h): Mean Encryption time

Results show that bio-inspired algorithm performs low with correlation test and takes more time for encryption. Self-adaptive algorithm is the fastest but lacks in performance with respect to UACI and entropy values. Face has an important significance in biometric based identification and authentication applications. However, the size of the images does not vary much and the need for real time transmission has limited scope. Hence, any of these algorithms can be chosen for encryption of this kind of images.

4.4. Results for Signature images

Fifty sample signatures are collected from fifty different people with a mobile app. Signatures are RGB images with size varying from 320×320 pixels to 675×675 pixels with white background. Performance parameters obtained for the fifty signature images are documented in Figures. 40 (a) to (f) and 41(a) to (h)

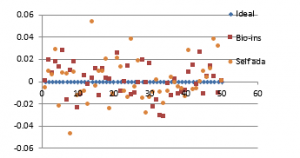
Figure 40(a): Horizontal correlation of fifty images

Figure 40(b): Mean Horizontal correlation

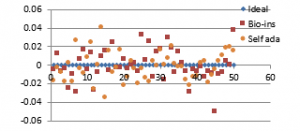
Figure 40(c): Vertical correlation for fifty images

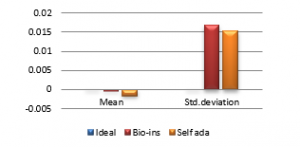
Figure 40(d): Mean vertical correlation

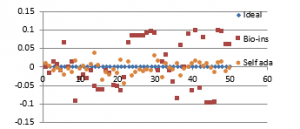
Figure 40(e): Diagonal correlation for fifty images

Figure 40(f): Mean Diagonal correlation

Below images Performance comparison for signature images from figure 41 (a) – (g)

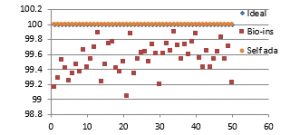
Figure 41(a): NPCR for fifty images

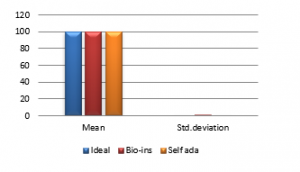
Figure 41(b): Mean NPCR

Figure 41(c): UACI for fifty images

Figure 41(d): Mean UACI

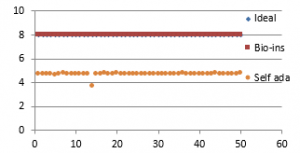
Figure 41(e): Entropy for fifty images

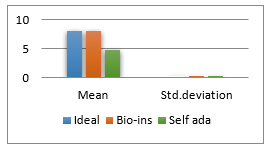
Figure 41(f): Mean Entropy

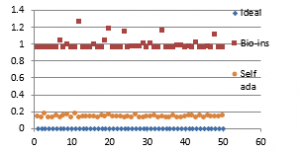
Figure 41(g): Encryption time for fifty images

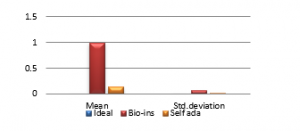
Figure 41(h): Mean encryption time

It can be observed that nature inspired encryption technique performs high for correlation, NPCR, entropy and UACI. Self-adaptive technique has high performance for correlation, NPCR and time, with entropy and UACI values deviating from the ideal values.

Signature images are mainly involved in online shopping and banking applications. Security of them is the primary factor rather than the time taken. Real time processing of these images has limited scope. Also, size of the signature images is not bulky and does not vary much. Therefore, nature inspired technique suits better for the signature image encryption in comparison with the self-adaptive technique.

5. Conclusion and future scope

Suitability analysis is performed on three datasets with different statistical features. Results obtained reveal that the bio-inspired technique provides better performance with respect to NPCR, UACI and entropy, but takes more time to encrypt. Self-adaptive encryption performs well in consideration with correlation and NPCR. Limitation of this method is its low performance in the UACI and entropy tests. Suitability analysis finds out that satellite images can be encrypted more efficiently using self-adaptive method. Performance is almost equal for face images. Signature image encryption can achieve better quality by using bio-inspired method and fast partial method.

1. M. Javidi and R. Hosseinpourfard, “Chaos Genetic Algorithm Instead Genetic Algorithm”, The International Arab Journal of Information Technology, . 12(2), 163-168, March 2015. https://doi.org/10.1007/s11633-017-1107-6
2. D. Haufu, L. Xiao-lu., L. Xue, “An Improved Genetic Algorithm for Combinatorial Optimization,” in Proceedings of the IEEE International Conference on Computer Science and Automation Engineering, Shanghai) 58-61, 2011. https://doi.org/10.1109/CEC.2014.6900496
3. K. Tang, “An Improved Genetic Algorithm based on A Novel Strategy for Nonlinear Programming Problems,” Computers and Chemical Journal, 35(3), 615-621, 2011. https://doi.org/10.1016/j.compchemeng.2010.06.014
4. F. Ye F., Y. Haiyang, and J. Xueshou, “An Improved Constrained Optimization Genetic Algorithm,” in Proceedings of IEEE International Conference on ICIS, Xiamen, China) 435-439, 2010. https://doi.org/10.1109/ICICISYS.2010.5658317
5. K. Shankar, P Eswaran, “An Efficient Image Encryption Technique Based on Optimized Key Generation in ECC Using Genetic Algorithm”, Artificial Intelligence and Evolutionary Computations in Engineering Systems, , 394, 705-714. https://doi.org/10.1007/978-81-322-2656-7_64.
6. H. Nematzadeh, RasulEnayatifar, bHomayunMotameni, Frederico GadelhaGuimarães, Vitor NazárioCoelho, “Medical image encryption using a hybrid model of modified genetic algorithm and coupled map lattices”, 110, 24-32, 2018. https://doi.org/10.1016/j.optlaseng.2018.05.009.
7. X. Wang, Hui li Zhang, “A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems”, Nonlinear Dynamics, 83, 333-346, 2016. https://doi.org/10.1007/s11071-015-2330-8.
8. Cheng T., Wang C., Xu M., and Chau W., “Optimizing Hydropower Reservoir Operation using Hybrid Genetic Algorithm and Chaos,” Water Resources Management, 22(7), 895-909, 2008. https://doi.org/10.1007/s11269-007-9200-1
9. Chao-Lin Kuo, et.al, “Image Encryption Based on Fuzzy Synchronization of Chaos Systems”, IEEE 37th Annual Computer Software and Applications Conference)45 3-461, 2013. https://doi.org/10.1109/COMPSAC.2013.23
10. Abdul Hanan Abdullaha, Rasul Enayatifara,, Malrey Lee, “A hybrid genetic algorithm and chaotic function model for image encryption”, International Journal on Electronics and Communication (AEÜ), 66, 806– 816,2012. https://doi.org/10.1016/j.aeue.2012.01.015
11. A. Ahmed et al., “Modeling and Simulation of Office Desk Illumination Using ZEMAX,” in 2019 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), 1–6, 2019. doi: 10.1109/ICECCE47252.2019.8940756.
12. V. Srikanth, et.al, “Bit-Level Encryption of Images using Genetic Algorithm”, TECHNIA, International Journal of Computing Science and Communication Technologies, 3(1), 2010. https://doi.org/10.1007/978-3-642-30111-7_75
13. K.A Al-Utaibi., El-Alfy, “A bio-inspired image encryption algorithm based on chaotic maps”, IEEE Congress on Evolutionary Computation (CEC)) 87-92, 2010. https://doi.org/10.1109/CEC.2010.5586463
14. Hassan Al-Mahdi , Yaser Fouad, “Design and analysis of DNA Binary Cryptography Algorithm for Plaintext”, International Journal of Engineering and Technology (IJET), 10(3) 699-706, 2018. https://doi.org/10.21817/ijet/2018/v10i3/181003055
15. Narendra K. Pareek, Vinod Patidar, “Medical image protection using genetic algorithm operations”, Soft Computing, 20(2), 763–772, 2016. https://doi.org/10.1007/s00500-014-1539-7
16. Yuansheng Liu,et.al, “Cryptanalyzing a RGB image encryption algorithm based on DNA encoding and chaos map”, Optics & Laser Technology, 60(6)111–115, 2014. https://doi.org/10.1016/j.optlastec.2014.01.015
17. H. Wen et.al, “Breaking an Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos’, Entropy, 21(7), 246-263, 2019. https://doi.org/10.3390/e21030246
18. A. Fatima, Isha Mehra and Naveen K Nischal , “Optical image encryption using equal modulus decomposition and multiple diffractive imaging”, Journal of optics, 18, 2016, 10.1088/2040-8978/18/8/085701.
19. R. Kumar, Basanta Bhaduri, “Optical image encryption using Kronecker product and hybrid phase masks”, Optics & Laser Technology, 95, 51-55, 2017. https://doi.org/10.1016/j.optlastec.2017.03.041
20. R. Kumar, Basanta Bhaduri, “Optical image encryption in Fresnel domain using spiral phase transform”, Journal of optics, Vol 19. 2017. 10.1088/2040-8986/aa7cb1
21. M. Joshi, Chandra Shakher, Kehar Singh, “Image encryption and decryption using fractional Fourier transform and radial Hilbert transform’, Optics and Lasers in Engineering, 46(1), 522– 526, 2008. https://doi.org/10.1016/j.optlaseng.2008.03.001
22. S. Liu, “A review of optical image encryption techniques”, Optics & Laser Technology, 57(1), 327–342, 2014. https://doi.org/10.1016/j.optlastec.2013.05.023
23. Z. Liu, et.al, “Color image encryption by using the rotation of color vector in Hartley transform domains”, Optics and Lasers in Engineering, 48, 800–805, 2010. https://doi.org/10.1016/j.optlaseng.2010.02.005
24. N. Singh, A. Sinha, “Optical image encryption using fractional Fourier transform and chaos”, Optics and Lasers in Engineering, 46(2) 117–123, 2008. https://doi.org/10.1016/j.optlaseng.2007.09.001
25. Y. Liang & G. Liu “Color image encryption combining a reality-preserving fractional DCT with chaotic mapping in HIS space”. Multimedia Tools and Applications, 75(11), 6605-6620, 2016. https://doi.org/10.1007/s11042-015-2592-7
26. Dr. Emad S. Othman, Dr. Mohammed M. Sakre, “Compression and Encryption Algorithms for Image Satellite Communication”, International Journal of Scientific & Engineering Research, 3(9), 1-4, 2012.
27. Qiwen Ran, et.al, “Vector power multiple-parameter fractional Fourier transform of image encryption algorithm”, Optics and Lasers in Engineering, 62, 80–86, 2014. https://doi.org/10.1016/j.optlaseng.2014.05.008
28. Ensherah A. Naeem, et.al, “Efficient implementation of chaotic image encryption in transform domains”, The Journal of Systems and Software, 97(3), 118–127, 2014. https://doi.org/10.1016/j.jss.2014.07.026
29. R. A. Schowengerdt, “Remote sensing, third edition: models and methods for image processing”, Academic Press, 2006.
30. Anil K. Jain, et.al, “Statistical Pattern Recognition: A Review”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000. https://doi.org/10.1109/34.824819
31. Panigrahi, Sushant, and Toran Verma, “Texture image classification using neuro fuzzy approach.” International Journal of Engineering and Computer Science, 2(1), 2309-2313, 2013.
32. Sura F. Yousif, “”Grayscale Image Confusion and Diffusion Based on Multiple Chaotic Maps”, 1st International Scientific Conference of Engineering Sciences – 3rd Scientific Conference of Engineering Science (ISCES), 2018. https://doi.org/10.1109/ISCES.2018.8340538
33. Jianhua Wu, Mengxia Zhang and Nanrun Zhou,“Image encryption scheme based on random fractional discrete cosine transform and dependent scrambling and diffusion”, Journal of Modern optics, 2016. https://doi.org/10.1080/09500340.2016.1236990
34. P. Maan, Hukum Singh, “Non-linear Cryptosystem for Image Encryption Using Radial Hilbert Mask in Fractional Fourier Transform Domain”, 3D Research, 9(53), 112-119, 2018. https://doi.org/10.1007/s13319-018-0205-8
35. V. Srikanth, et.al, “Bit-Level Encryption of Images using Genetic Algorithm”, TECHNIA, International Journal of Computing Science and Communication Technologies, 3, issue1, 2010.
36. R. Bhagyashri. Pandurangi, Meenakshi R. Patil, “A Nature Inspired Color Image Encryption Technique to Protect the Satellite Images”, International Journal of Current Engineering and Technology, 9(3), May 2019. https://doi.org/10.14741/ijcet/v.9.3.4
37. R. Bhagyashri. Pandurangi, Meenakshi R. Patil, Chaitra Bhat, “Comparison of Bio-inspired and Transform based Encryption Algorithms for Satellite Images”, Third IEEE International Conference on Electrical, Electronics, Communication, Computer Technologies and Optimization Techniques (ICEECCOT), Mysore, India, December 2018. https://doi.org/10.1109/ICEECCOT43722.2018.9001344
38. H. Gao, et.al, “A new chaotic algorithm for image encryption”, Chaos, Solitons& Fractals, 2(29), 393-399, July 2006. https://doi.org/10.1016/j.chaos.2005.08.110
39. Adolf W. Lohmann, David Mendlovic, and Zeev Zalevsky, “Fractional Hilbert transform,” Optics Letters, 21(4), 281-283, 1996. https://doi.org/10.1364/OL.21.000281
40. https://bhuvan-app1.nrsc.gov.in/imagegallery/bhuvan.html
41. http://cmp.felk.cvut.cz/~spacelib/faces/faces94.html

(Click Here)

(Click Here)