1 Introduction

The need for robust robotic controllers, that respond to greater productivity and faster manufacturing devices, has been a hot topic in the last few years. This need obviously imposes high pressure on researchers to acquire secure and effective robots, especially with the increasing humanitarian and social exigency, which require interactions between robots and humans. This paper presents an extension of a research work originally presented in the 8^th International Conference on Modelling, Identification and Control [1]. Recently, several similar synchronization studies have been investigated in several complex mechanical systems, where flexibility a nd accuracy have been highly recommended [2], [3], [4], [5], [6]. There exist numerous samples of sophisticated technologies dedicated to modern life, such as material transporting [7], [8], advanced agriculture aggregation [9], building tasks [10], etc. Indeed, in light of the accelerated pace of development, there has become a growing demand for cooperative multi-agent robotic systems to serve contemporary industries and manufacturing applications [11], [12]. In this context, it has been proved that the flexibility and the maneuverability guaranteed by a cooperative robotic system are far beyond the working capacity of one single manipulator. In the other hand, the time-delay phenomenon obviously appears in nature [13], especially in several control systems (aircraft, chemical or process control systems) either in the control input, in the state or in measurements. In contrast to the ordinary differential equations, delayed systems are infinite dimensional in nature, and the time-delayeddatatransmissionpresentsinthemostofcases,asourceofinstability.Asanillustration,astateestimatorisdesignedin[14]toaclassofuncertaindiscrete-timeMarkovianjumpneuralnetworks,withtime-varyingdelays,inordertoestimatethenetworkstatesthroughavailableoutputmeasurements.Indeed,thestudypresentedin[15]seekstoresolvetheproblemofdatapacketdropoutandtransmissiondelaysresultedbycommunicationchannelsinthe

networkedcontrolsystem.So,greate ortshavebeeninvestedinthesynthesisofuncertainnetworkedsystemswithtime-delay,seenthatthestabilityissueaswellasperformancesofthesystemcontrolwithdelayarebothoftheoreticalandpracticalimportance.However,inseveralroboticapplications,theuncertaintymayarisefrommanyrealworldsourcessuchaserrorsoftherobotmodeling,unpredictablerobotactuation,unpredictablemovementsintheenvironment,etc[16],[17].Aswell,whilerobotsareexecutingtheirassignedglobaltask,someassumptionsunderwhichcontrollerswerebuilt

may be invalidated: loads or robots may fail, the environment may change, etc. The cumulative e

ect of

513

such uncertainty sources can be hard to manage during the task execution. Thus, to ensure a fluid response to the distributed multi-robot system, tradeoffs between multi-robot flexibility, time delay adjustment, uncertainty compensation, and task execution efficiency should be considered. To achieve it, we present, as a first step, the stability analysis and then the simulation results of a robust control concept, which combines the SMC design with a partic-ular class of the graph theory, aiming to stabilize a networked robotic system.

2 Introduction to the SMC

While considering the SMC concept, the state trajectory evolution is divided into two parts [18]:

• from the initial state to the intersection with thesliding surface, this part is called “the reaching phase”,
• from the intersection with the sliding surface tothe origin, this part is called “ the sliding phase”.

During the reaching phase, the attractiveness condition of the sliding surface S˙(x)S(x) < 0 is verified. This condition is global but it does not guarantee a finite sliding time. To ensure a finite sliding time, the condition becomes:

                 S˙(x)S(x) < −ε₁ − ε₂|S| if S(x) , 0 and ε > 0              (1)

This sliding time can be imposed by choosing the sliding surface of the form:

                            S˙(x) = −µS(x) − µΩsign[S(x)]                         (2)

This expression, which has been adopted in this study, is a solution of a differential equation [19]. During the sliding phase (S(x) = 0 and S˙(x)S(x) < 0), the closed loop system has the same behavior than S(x) = 0. In general, for a system of order n which is described in the state space by:

⁽ x˙_i = x_i+1 i = 1,…,n ⁻ 1 (3) x˙_n = f (x,t)+g(x,t)u(t)

the linear sliding surface according to the state has the form:

n

X

                                    S(x) = Cx =           c_ix_i                                                (4)

i=1

In the sliding phase, the looped system will have the same behavior as the system is described by:

^_ x˙_i = x_i+1 ;i = 1,…,n ⁻ 2

 − −nP−1cixi ;cn = 1 (5) x˙n 1 =

                           ^                   i=1

This is a linear system of order (n−1) [20]. Thus, when the sliding regime is reached (after an interval t_g of time), the operating point is going to stay on the surface whose equation is S(x) = 0. Therefore, the looped system has an insensitivity to parameter variations of the system to be controlled.

3 Problem formulation and Mutual SMC synchronization concept

Let us consider p manipulator robots described by the following differential equation:

                       M_i(q¨_i)+C_i(q_i,q˙_i)q˙_i +G_i(q_i)         =     τ_i                      (6)

for i = 1···p. Each robot has n degrees of freedom, for which:

• q_i ∈ _Rⁿ denotes the vector of measured displacements and i is the number of cooperative robots, • q˙_i ∈ _Rⁿ is the measured velocity vector,
• q¨_i ∈ _Rⁿ is the vector of articulatory acceleration, • M_i(q_i) ∈ _R^n×n is the inertia matrix, which is symmetric uniformly bounded and positive definite,
• C_i(q_i,q˙_i)q˙_i ∈ _Rⁿ is the vector expressing the Coriolis and the centrifugal forces,
• G_i(q_i) ∈ _Rⁿ is the vector of gravitational forces,
• τ_i ∈ _Rⁿ denotes the vector of external torques and forces applied at each joint.

The state vector is presented as: x_i = ^q_q˙ⁱ_i!, and its control vector is u_i = τ_i. To achieve a coordinated control motion, a cross coupling synchronizing approach (that is derived from the graph theory [21]) has been applied to the networked system. Thus, the cross-coupled SMC concept is adopted in this work to control the whole multi-agent system, which in turn becomes considered as a single generalized system. The typical procedure for implementing such a control module is to first build a global error model in real time [3], based on the information feedbacks derived from all system members. In order to achieve this goal, we define the tracking error as follows:

                                     ζ_1i(t) = q_i(t) − q_d(t)                                (7)

where:

• q_d(t) ∈ _Rⁿ denotes the desired position of the robot.

The ‘cross-coupling’ concept consists in presenting a synchronization error with reference to the calculation of differences between position errors. This error is presented as follows [3]:

p

X

                    ζ₂i(t)      =              Λij [q_i(t) − q_j(t − τ)]                 (8)

j,i

global error concerning each agent of the system is given by:where Λ_ij = Λ_ji are symmetric positive-definite matrices which reveal an idea about the communication quality between the i^th and j^th agent. Finally, the

Z t

εi = ζ1i +           ζ2i(µ)dµ 0 Let’s consider the sliding surface: si = ε˙i +λiεi and let’s define the control law:	(9)
ui = ueq +∆u	(10)

Hence, equality s˙_i = 0 yields the following equivalent control expression:

ueq = Mihq¨id −ζ˙2i −λi(ζ2i −ζ˙1i)i+Ci(qi,q˙i)q˙i +Gi (11) and the discontinuous control part becomes:

                                  ∆u = −M_i⁻¹ K_i sign (s_i)                           (12)

where K_i is a definite positive diagonal matrix.

Applying the control law (10) yields the expression of the differential with respect to time of vector s_i:

                                        s˙_i = −K_i sign(s_i)                                 (13)

The advantage of the adopted decentralized architecture is that it allows to each robot to have local information about relative positions of its neighbors. So each agent can communicate and share information with robots placed just nearby, according to the utilized cross coupling approach.

• Stability analysis

To prove the stability of one agent in the system, we consider a Lyapunov function:

12              T Ki−1si        > 0          (14) Vi       =              si

Its differentiation with respect to time gives:

                            V˙_i        =        −s_i^T sign(s_i) < 0                         (15)

By considering the whole multi-agent system, the chosen Lyapunov candidate function becomes:

p

X

                                       V =           V_i > 0

i

and after its differentiation with respect to time we obtain:

p

V˙ = ^−X s_i^T sign(s_i) < 0

i

This proves the stability of the overall system.

• Convergence to the desired trajectory

It is clear that s_i(t) goes to zero after the reaching phase (t > t₀). In the sliding phase, we have s_i = 0. That is for t > t₀:

εi(t)     =       εi(t0)e−λ(t−t0)	(16)
ε˙i(t)     =       −λεi(t0)e−λ(t−t0) It is obvious that:	(17)
lim εi(t)       =     0 t−→+∞	(18)
lim ε˙i(t)      =     0 t−→+∞	(19)

Then, we can write that for t > t₁ = t₀ + _λ⁵:

                                      ε_i(t) ‘ 0 , ε˙_i(t) ‘ 0                               (20)

Let’s assume that the following quantities are uniformly bounded for t > t₁:

	kqd(t) − qd(t − τ)k	≤	m1	(21)
	kq˙d(t) − q˙d(t − τ)k	≤	m2	(22)
Z t	qd(ς) − qd(ς − τ)dς	≤	m3	(23)

                       t−τ                                                         

Let’s write, for t > t₁, ε˙ = 0:

                                                              



q˙i(t) − q˙d(t)+XΛij[qi(t) − qd(t)]

                                                              

  j,i

X

− Λ_ij [q_j(t − τ) − q_d(t − τ)] j,i

X + Λij [qd(t) − qd(t − τ)] = 0 j,i Denoting:	(24)
X di(t)    =              Λij[qd(t) − qd(t − τ)]	(25)

j,i

we can write that:

                            

ζ˙1i(t)+XΛijζ (t)−XΛijζ1j(t −τ)+di(t)=0 (26)

1i

                            

                            

                   j,i                                         j,i

Let’s define: ζ₁ = [ζ₁^T_i ζ₂^T_i ··· ]^T and d = [d₁^T d₂^T ··· ]^T . Then, we have:

                            ζ˙₁(t) = Aζ₁(t)+Bζ₁(t − τ)+d(t)                     (27)

where A is a block-diagonal matrix, for which each bloc-diagonal term is:

p

X

A_i = − Λ_ij                (28) j,i

which is a symmetric definite negative matrix. This shows that all eigenvalues of matrix A_i have strictly negative real parts. Consequently, A is a Hurwitz matrix.

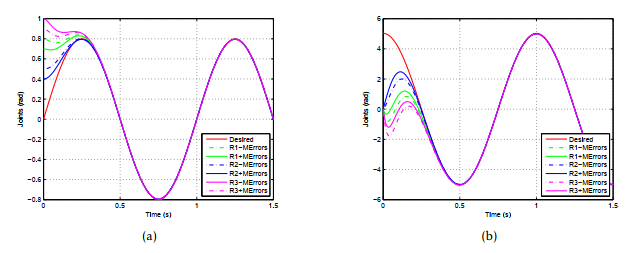Figure 1: The 1^st joints SMC:(a) Trajectory tracking and position synchronization,(b) Velocity synchronization.

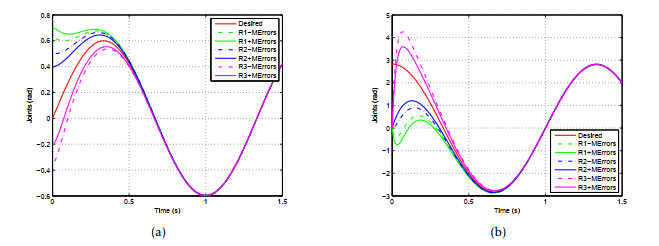 Figure 2: The 2^nd joints SMC:(a) Trajectory tracking and position synchronization,(b) Velocity synchronization.

Table 1: Joints initiation and parameters

Articulation	Mass	Length
q1	8 kg	0.4 m
q2	6 kg	0.3 m
q3	0.5 kg	0.3 m

Using properties of matrices A and B, and using the fact that d(t) is uniformly bounded, we can deduce that ζ₁(t) is uniformly bounded [22, 23, 24]. This shows that ζ_2i(t) and:

Z t

ζ2i(t)dt = εi − ζ1i(t) 0 are uniformly bounded. This yields that:	(29)
lim ζ2i(t) = 0 t−→+∞ In consequence, we have, for t > t1:	(30)
ε(t) = ζ˙1i +ζ2i ‘ 0	(31)

Finally, we can easily deduce that for t > t₁:

ζ₁(t) ‘ 0. This proves that positions of al robots converge to their desired trajectory.

• Application

Consider the SMC law applied to the networked robotic system for a trajectory tracking control task. Here, the cooperation is defined as a group of robots that work together to accomplish a required task, where resources are shared between all agents, and the action performed by each robot takes into account actions performed by others. The required behavior of the proposed synchronizing SMC is to handle measurement errors appearing in the controller of one robot in the system, the communication time delay lag between cooperative robot movements, and at the same time to retain all properties and system performances. So that, the designed controller must have a sufficient authority which is able to dominate the undesirable disturbances affecting one robot, and which Without external disturbances,

have been transmitted to other neighbors due to the feedback control sharing imposed by the cross coupling design. Dynamic parameters of the manipulator robot model are mentioned in Table I. We note that:

• R_i: designate the cooperative robots, i = 1..
• R-MErrors: presents the robot behavior without measurement errors ( in the presence of a constant communication time delay z = 0.4s).
• R+MErros: presents the robot behavior in the presence of measurement errors affecting the position vector of the first robot R1 ( in the presence of a constant communication time delay z = 0.4s).

Discussion: Simulation results present a comparison between behaviors of the time-delayed networked system acting with and without presence of measurement errors. The robust synchronization of the networked system, realized by the synchronizing SMC has been proved when the time delay rate is valued around 0.4 s, even in the presence of external disturbances. In fact, position and velocity behaviors of the multi-agent system are almost similar in both cases as shown in Figs.1, 2 and 3, despite the addition of measurement errors (at the position vector of the first robot) whose impact reaches 20% of its right value. So the global system addresses imposed perturbations and different positions of cooperative robots rapidly attain their desired trajectories. At the same time, the synchronization effect is clearly presented despite the existence of communication time delay between robots. Besides, the generated velocity curves also reflect the insensitivity of the proposed control approach to different perturbations applied to the system, as demonstrated in Figs.1(b), 2(b) and 3(b). This proves the robustness of the synchronizing SMC in achieving adequate motion control and meeting the efficiency requirement throughout a middle affected by a constant communication time-delay and relatively high valued external disturbances. Concerning the control input behavior, we note that the signum function (which is responsible to generate the chattering phenomenon) has been replaced by an approximating function (Hyperbolic tangent) in order to better present the disturbance effect on the system. This is justified by the fact that the high frequency signals resulted from the chattering phenomenon cover the measurement error impact, whose amplitude is much smaller in comparison with the chattering one. So in the absence of measurement errors, torques behave smoothly as shown in Fig.4(a) and obviously in Fig.4(b). However, it is clear that input torques are influenced by the presence of disturbances, where slight oscillating signals disrupt input torques of the affected robot, and lower disturbing signals appear in the torque behaviors of other agents not affected. This shows that each robot influences other teammates under the synchronizing control effect. So, feedbacks derived from unaffected robots help the affected agent to overcome external disturbances which he meets.

• Conclusion

In this paper, we have developed an analytical approach to define a dequate s ynchronizing stability conditions in the presence of constant communication delays, and illustrated them for a decentralized architecture of a class of networked robotic systems. This analysis shows that the overall system synchronization, even in a middle disturbed by measurement errors, can be successfully guaranteed by transmitting feedbacks between cooperative system agents. Obtained comparison between simulation results shows that the networked system can easily reach desired behaviors and move smoothly when the considered communication time delay is valued around 0.4 s, and the rate of measurement errors attain 20%. The presence of low disturbing frequencies in the control torques of agents proves that the proposed controller addresses distur-bances and guarantees a robust synchronized motion task. Further researches will involve consideration of the system convergence rate with respect to the time-varying delay functions, to the SMC constraints, and to the limit

1. F. Abdelhedi, A. Jribi, & N. Derbel, Robust SMC for synchronization of networked time delay robotic systems. 8th International Conference on Modelling, Identification and Control (ICMIC), 2016.
2. M. Fathallah, F., Abdelhedi, & N. Derbel, A surveillance camera algorithm based on the sliding mode approach with measurement’s disturbance. The 13th International Multi-Conference on Systems, Signals and Devices (SSD), 783–786, 2016.
3. D. Sun, Synchronization and control of multi-agent systems, vol. 41. CRC Press, 2010.
4. F. Abdelhedi, Y. Bouteraa and N. Derbel, Second Order Sliding Mode Based Synchronization Control for Cooperative Robot Manipulators, Advances and Applications in NonlinearControl Systems Springer International Publishing, 2016.
5. F. A. Bouaziz, Y. Bouteraa, and N. Derbel, Control energy comparison between 1st and 2nd order sliding mode approach with application to a SCARA robot, In 13th International Multi-Conference on Systems, Signals and Devices, 2016.
6. P. Gratia, A. Magomedov, T. Malinauskas, M. Daskeviciene, A. Abate, S.Ahmad, … & M. K. Nazeeruddin, A Methoxydiphenylamine Substituted Carbazole Twin Derivative: An Efficient Hole Transporting Material for Perovskite Solar Cells. Angewandte Chemie International Edition, 54(39), 11409–11413, 2015.
7. Y. K. Wang, Z. C. Yuan, G. Z. Shi, Y. X. Li, Q. Li, F. Hui, … & L. S. Liao, DopantFree Spiro Triphenylamine/Fluorene as Hole Transporting Material for Perovskite Solar Cells with Enhanced Efficiency and Stability. Advanced Functional Materials, 26(9), 1375–1381, 2016.
8. A. Z. Abbasi, N. Islam, & Z. A. Shaikh, A review of wireless sensors and networks’ applications in agriculture. Computer Standards & Interfaces, 36(2), 263–270, 2014.
9. C. Laschi, & M. Cianchetti, Soft robotics: new perspectives for robot bodyware and control. Frontiers in bioengineering and biotechnology, 2(3), 2014.
10. A. Jribi, F. Abdelhedi, Y. Bouteraa, and N. Derbel, Kinematics and a Comparison Between Two SM Control Strategies for a 5DOF Serial Robot for Tele-Echography. In Applications of Sliding Mode Control 157–174. Springer Singapore, 2017.
11. S. J. Chung, U. Ahsun, J. J. E. Slotine, D. W. Miller, Application of synchronization to cooperative control and formation flight of spacecraft, In proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit. Hilton Head, South Carolina, 2007.
12. M. Wu, Y. He, and J. H. She, Stability analysis and robust control of time-delay systems, 43–47. Berlin: Springer, 2010.
13. P. Shi, Y. Zhang, & R. K. Agarwal, Stochastic finite-time state estimation for discrete time-delay neural networks with Markovian jumps. Neurocomputing, 151, 168–174, 2015.
14. M. Yu, L. Wang, T. Chu, & F. Hao, Stabilization of networked control systems with data packet dropout and transmission delays: continuous-time case. European Journal of Control, 11(1), 40–49, 2005.
15. R. Olfati Saber, Flocking for multi agent dynamic systems: algorithms and theory. IEEE Transactions on Automatic Control, 51(3):401–420, 2006.
16. B. Yang, & H. Fang, Forced consensus in networks of double integrator systems with delayed input. Automatica, 46(3), 629–632, 2010.
17. A. S. Nouri, F. A. Bouaziz, and N. Derbel, On the Sliding Control, In Applications of Sliding Mode Control Springer Singapore, 2017.
18. F. Abdelhedi, N. Derbel, Adaptive Second order sliding mode control based cross coupling concept for synchronization of robotic systems, Advances in Systems, Signals and Devices, Issues on Systems, Analysis and Automatic Control, 2016.
19. P. Lopez & A.S. Nouri, Thorie lmentaire et pratique de la commande par les rgimes glissants, Mathmatiques et applications 55, SMAI, Springer – Verlag, 2006.
20. M. C. Golumbic, Algorithmic graph theory and perfect graphs 57, Elsevier, 2004.
21. N.N. Krasovskii, Stability and motion: applications of Lyapunov’s second method to differential systems and equations with delay. Stanford University Press, Stanford, 1963.
22. Gu. K. Discretized lmi set in the stability problem of linear uncertain time-delay systems, International Journal of Control, 68:923–934, November, 1997.
23. Gu. K. An integral inequality in the stability problem of time-delay systems, In Proceedings of the 39th IEEE Conference on Decision and Control, 3:2805–2810, 2000.
24. Y. Miladi Siala, Commande du comportement chaotique d’un moteur pas pas. Master report, Ecole Nationale d’Ingnieurs de Sfax-Tunisia, June, 2012.

(Click to view)

(Click to view)