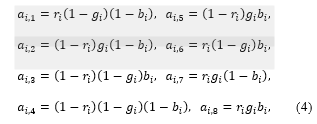1. Introduction

The reflectance properties of object surfaces are determined by the spectral reflectance factors that are normally measured at regular intervals in the visible spectrum of radiation by reflectance spectrophotometers [1]. The integrals of the products of the spectral reflectance, the relative spectral power distribution of an illuminant and color matching functions produce the tristimulus values. On the other hand, the inverse computation from tristimulus values or colorimetric data to the spectral reflectance is a difficult problem because the computation of tristimulus values from spectral reflectance involves the dimensionality reduction of data, i.e., the spectral reflectance estimation is an ill-posed problem.

Recently, Sharma and Wang proposed a neural network-based spectrum recovery method, and evaluated the accuracy of the spectrum recovery by the spectral mean-squared error [2]. Harifi et al. presented a principal component analysis (PCA)-based method which employed six principal components [3]. Amiri and Amirshahi proposed a step by step progressive method for recovery of spectral data from the corresponding colorimetric information, where the spatial dimensions are decreased from 6D to 3D in a step-by-step manner to decrease the number of samples used for color gamut interpolation [4]. Wu et al. presented an approach that uses a new sample selection criterion based on color feature match to select a series of suitable samples for creating the adapted transformation matrix to reconstruct spectral reflectance [5]. Inoue et al. proposed two methods for recovering the reflectance spectra of colorimetric data by using the non-negative constraints in reflectance spectra, where the problem of reflectance spectra recovery is formulated as a nonnegative least squares problem [6] into which the Neugebauer model [7] is incorporated [8]. These methods can be used to estimate the spectral reflectance from general colorimetric data including CIE tristimulus values and CMYK-printed samples.

The Neugebauer model can be used to infer the gamut boundaries of printed colorants on paper [7] by printers such as conventional CMYK printers. If three inks, such as cyan, magenta and yellow, are utilized, then the paper may be covered by one ink, two inks, three inks, or may be left blank. As a result, eight combinations of overlap of inks can occur, and they correspond to eight basic colors, such as red, green, blue, black, cyan, magenta, yellow and white, which are referred to as the Neugebauer primaries [7]. Although the Neugebauer model was originally developed for modeling the printed colorants on paper, it can be used for general colorimetric data as we will prove in Subsection 2.1 that the equation of the Neugebauer model holds for any color in RGB color space.

The rest of this paper is organized as follows. Section 2 summarizes the Neugebauer model, and then proposes the sparse Neugebauer model. Section 3 proposes a method for estimating the spectral reflectance based on the Neugebauer models, and a convergence property of the proposed estimation algorithm is proved. Section 4 describes the procedure for reproducing the colors from the estimated spectral data. Section 5 shows experimental results. Finally, Section 6 concludes this paper.In this paper, we propose sparse Neugebauer model for estimating spectral reflectance of Neugebauer primaries or basic eight colors when reflectance spectra of several colors are given. Experimental results show that the proposed method achieves lower estimation error than the previous method with the conventional Neugebauer model. We also reproduce the Neugebauer primaries and the colors of given reflectance spectra from the estimated reflectance spectra. The effectiveness of the sparse Neugebauer model in color reproduction is also demonstrated in comparison with the conventional Neugebauer model.

2.       Neugebauer Models

In this section, we first summarize the Neugebauer model, and then propose sparse Neugebauer model to improve the performance of spectral reflectance estimation and color reproduction.

2.1.  Neugebauer Model

Let  be a color vector in RGB color space (bold italic lowercase letters denote vectors), where  and  denote the red, green and blue components of the color, and satisfy  and , respectively. Then  have another expression as follows:

  (1)

where  and  denote the Neugebauer primaries [7]: red, green, blue, black, cyan, magenta, yellow and white, respectively. The coefficients in (1) are given by

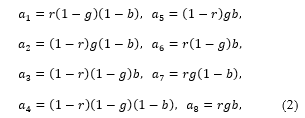which are called the Demichel equations, and (1) is called the Neugebauer equation [7]. The coefficients in (2) are nonnegative and satisfy  where . The equality in (1) with the coefficients in (2) can be confirmed for each element as follows: for example, the first element in (1) satisfies

The similar equations hold for the second and third elements in (1).

      We simply call (1) with (2) the Neugebauer model, which is valid for both tristimulus values and spectral reflectance, and use it for spectral reflectance estimation.

2.2.  Sparse Neugebauer Model

      Let  be a set of the Neugebauer primaries. Then the Neugebauer equation in (1) states that an arbitrary color vector  can be expressed as a weighted average of the eight color vectors in . We can also express a color vector in RGB color space as a linear combination of four colors which are in general position in RGB color space because four points being in general position in a three-dimensional color span a three-dimensional linear space, and form a tetrahedron. If a color is just on a plane spanned by three vertices of RGB color cube or a line connecting two vertices of RGB color cube, then the color is expressed as the linear combinations of three or two vertices, respectively. We describe the most general four-color case as follows (in the other degenerated cases, the description can be simplified): Let  be a subset of  the elements of which are in general position. Then, for a color vector , we have from which the coefficients  are given by

where  is selected as a basic point. As a result, we have

                                        where , and the four coefficients are nonnegative if  is in the tetrahedron with the four vertices in . We call (3) the sparse Neugebauer model since four coefficients among eight ones in (1) are zero in (3).

We adapt the minimal brightness variation criterion (MBVQ) proposed by Shaked et al. [9] for selecting four Neugebauer primaries , which are called the minimal brightness variation quadruple (MBVQ) [9], and given by  or .

3.       Spectral Reflectance Estimation

Assume that the reflectance spectra of  colors  for  are given and stored in , where  denotes the reflectance of the th wavelength  for  in the th color . Then, by the above nonsparse or sparse Neugebauer model, we have

where  denotes an  coefficient matrix whose elements are given by

 (4)

when the Neugebauer model is used, and these are the Demichel equations [7] for the th color , and the number of columns in  is the number of the Neugebauer primaries, i.e., . For the sparse Neugebauer model, four coefficients out of the eight ones in (4) become zero.  denotes a  matrix whose  element  is the reflectance of the th Neugebauer primary at the th wavelength . Then we formulate the problem for estimating the spectral reflectance of the Neugebauer primaries as follows:

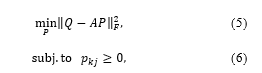where  denotes the Frobenius norm, and the constraint (6) is for  and . Let  be the objective function in (5), then we have

Since  is a constant independent of , the minimization of  is equivalent to the maximization of

      Applying Jensen’s inequality [10] to the second term of the right side in (7), we have

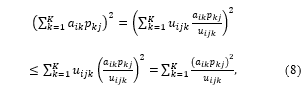where  are positive constants satisfying . Substituting the rightmost term in (8) into (7), we have a lower bound of  as

where  denotes a three-dimensional array having  as its  element.

      Replacing  with , we formulate the problem of spectral reflectance estimation as follows:

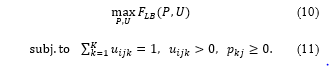Let  be the Lagrange function for the constrained maximization problem (10) with (11), where  for  and  are the Lagrange multipliers. Then we have the following condition for optimality:

where  and  denote the element-wise multiplication and division, respectively, because    and  in (15) are the  elements of matrices  and  in (16), respectively.

Proposition 1 The sequence  converges.

Proof. Let

                                                                       (17)

be an instance of  substituted  for  in (14). Then (15) can be written as

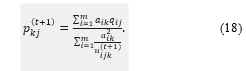                                                                  Since (17) is the solution to  and  with , we find that . Similarly, since (18) is the solution to  with , we find that , i.e.,

                              Next, substituting (14) into (9), we have

from which and (19) we have

                                           Considering the relationship between  and  given by , we have the following inequality from (20):

that is, the sequence  is monotonically nonincreasing, and is also bounded below by , i.e.,  by definition. Consequently, the sequence  converges to a number greater than or equal to .

4.       Color Reproduction

Let  and  be the color matching functions for the 1931  CIE standard colorimetric observer [], where  denotes a wavelength, and let  be the relative spectral power distribution of an illuminant. Then the CIE XYZ tristimulus values of a spectral reflectance  are given by

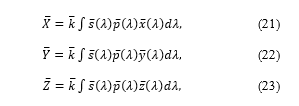where  is a normalizing factor given by . We use the trapezoidal rule for computing the above integrals. The transformation from the CIE XYZ tristimulus values into the standard RGB (sRGB) is as follows. First, we compute the linear transformation where note that similar but slightly different transformation matrices are also proposed and used in practice.

      Next, a nonlinear luminance encoding, which is also known as gamma encoding, is calculated to obtain sRGB values as follows:

Consequently, we obtain the sRGB values  transformed from the CIE XYZ tristimulus values .

5.       Experimental Results

      In this section, we show experimental results of spectral reflectance estimation and color reproduction. Figure 1 shows the Macbeth ColorChecker (MCC), of which the manufacturer’s sRGB D65 color values are also given on the Internet (ColorChecker, Wikipedia. URL: https://en.wikipedia.org/wiki/ ColorChecker). Although the 24 squares of painted samples in MCC are not materials but colorants, the proposed method can handle both of them equally because the Neugebauer model is valid for general colorimetric data as shown in Subsection 2.1.

Figure 1 Macbeth ColorChecker.

The spectral reflectance data of the 24 colors in MCC are shown in Figure 2, where the line colors correspond to the MCC colors. These data are provided by the Munsell Color Science Laboratory (URL: http://www.cis.rit.edu/research/mcsl2/online/cie.php).

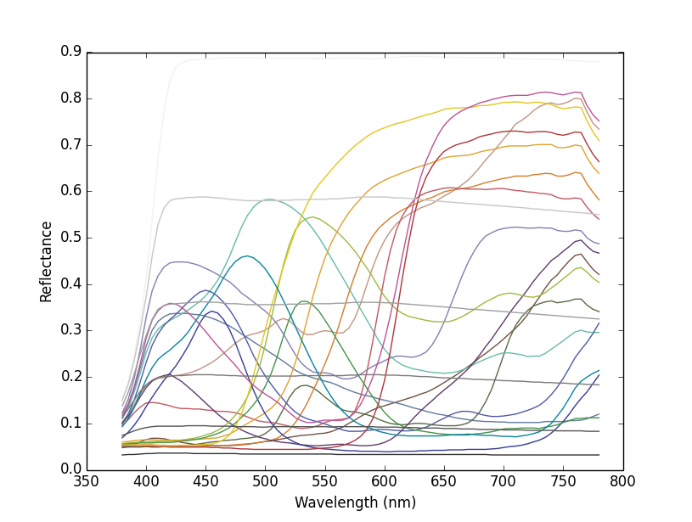Figure 2 Reflectance spectra of Macbeth ColorChecker colors.

      In the following experiments, we store the above data in a matrix  where  denotes the number of colors in MCC, i.e., , and  denotes the number of spectral data in which the wavelengths between 380 nm (nanometer) and 780 nm are sampled at 5 nm intervals, i.e., .

     Figure 3 shows the change in the value of the objective function  of the proposed method with the Neugebauer model described in Section 2.1, where the vertical and horizontal axes denote the objective function value and the number of iterations  with the maximum iteration number , respectively. The objective function value monotonically decreases with the increase in the number of iterations, that supports the claim in Proposition 1 experimentally.

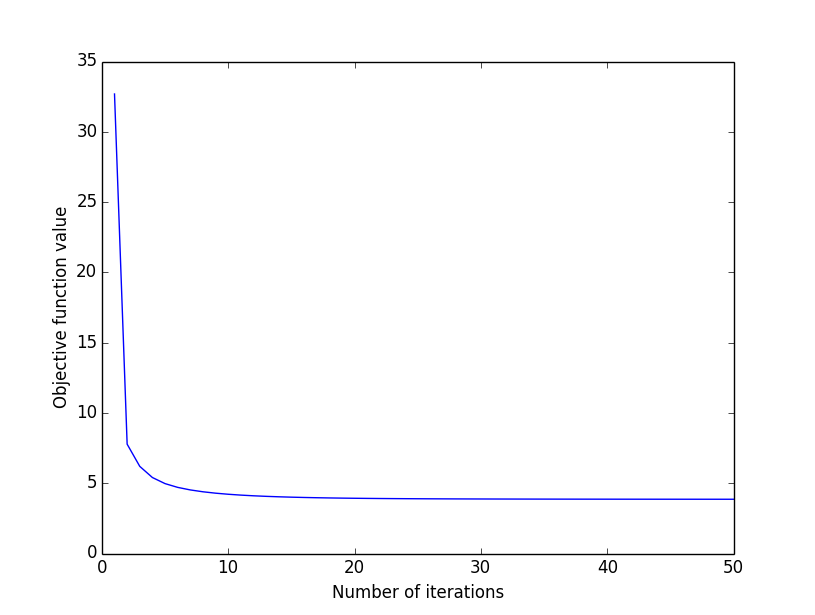Figure 3 Change in objective function value.

      Figure 4 shows the estimated spectral reflectance of the Neugebauer primaries by the sequential coordinate-wise algorithm (SCA) [6,8], where the vertical and horizontal axes denote the reflectance and wavelength, respectively, and the colors of solid lines correspond to the primary colors, and the broken line denotes white color. On the other hand, Figure 5 shows the estimated spectral reflectance by the proposed method with the Neugebauer model, and is similar to Figure 4, although the algorithms are different from each other. We measured CPU time for estimating the spectral reflectance on an Intel Core-i3-equipped PC using Portable Python 2.7.6.1. Then SCA and the proposed method required 1.12 and 0.028 seconds, respectively, from which we conclude that the proposed method is computationally more efficient than SCA.

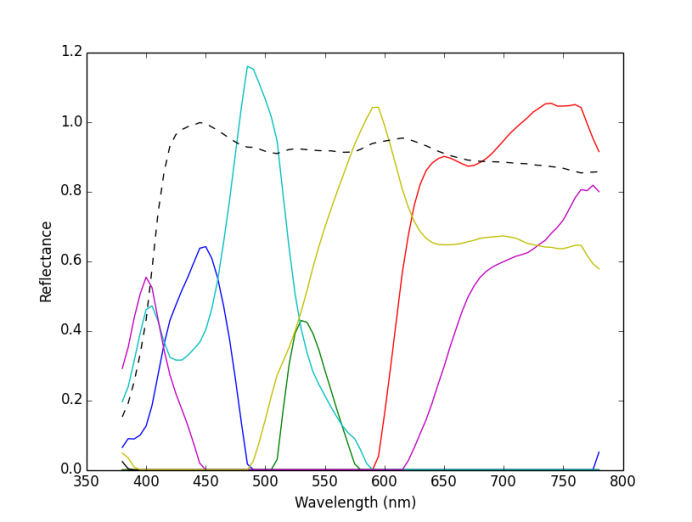Figure 4 Estimated spectral reflectance by SCA [6,8].

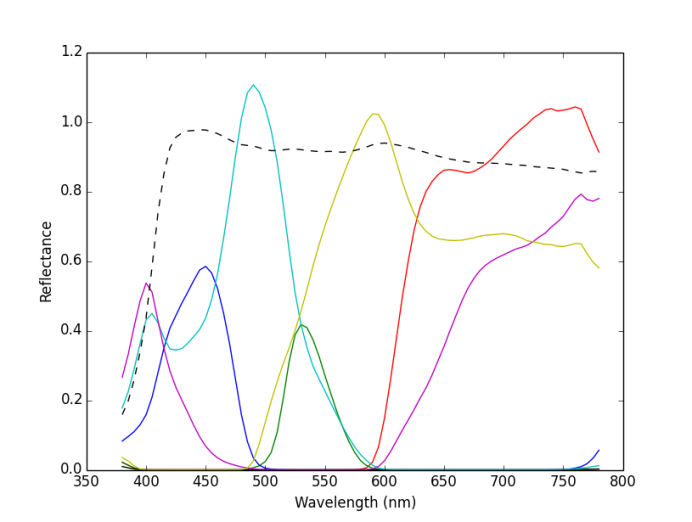Figure 5 Estimated spectral reflectance by the proposed method with Neugebauer model.

      Next, we compare sparse Neugebauer model with nonsparse or conventional Neugebauer model in the proposed method. Figure 6 shows the coefficients in two Neugebauer models for the upper left color in MCC in Figure 1, where the vertical and horizontal axes denote the value of each coefficient and the Neugebauer primaries, respectively. the blue and red bars denote conventional (nonsparse) and sparse Neugebauer models, respectively. In the conventional model (blue bars), all Neugebauer primaries have positive values. On the other hand, in sparse one (red bars), only four colors (R, G, B and M) have positive values, and the other coefficients are strictly zero.

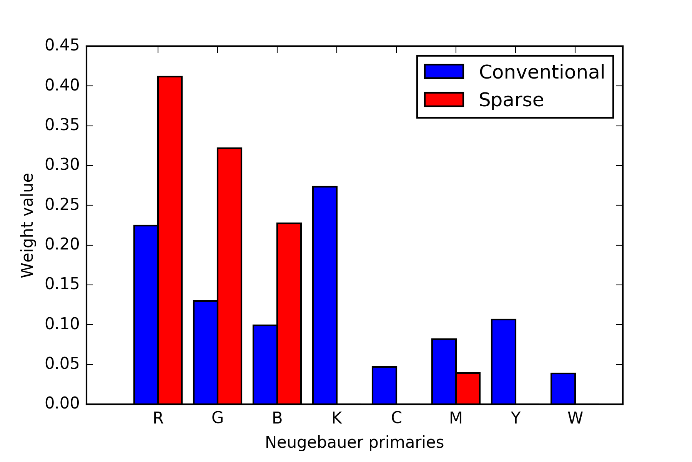Figure 6 Coefficients in Neugebauer models.

      Figure 7 shows the estimated spectral reflectance of the Neugebauer primaries by the proposed method with the sparse Neugebauer model. Each curve in Figure 7 has greater variance than that in Figure 5 or 4.

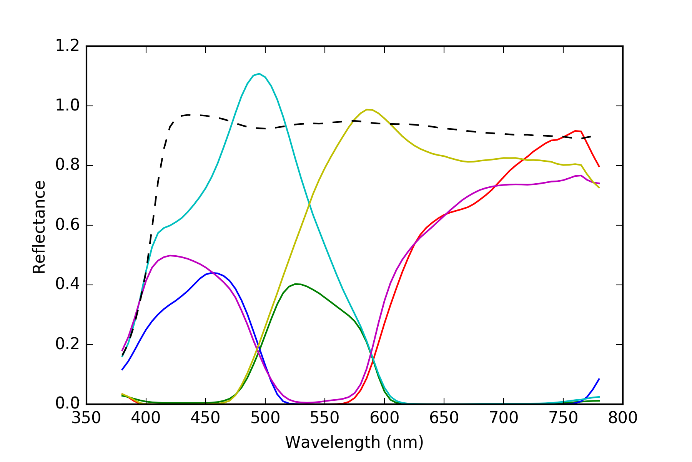Figure 7 Estimated spectral reflectance by the proposed method with sparse Neugebauer model.

      From Figure 8 to Figure 11, we show the reflectance spectra of the colors in MCC from the first to fourth rows, respectively (here we divide the 24 MCC colors into 4 figures each of which includes the spectral reflectance curves of 6 colors for visibility), where solid lines show the original reflectance spectra, and broken lines show their estimated ones by the proposed method with the Neugebauer model.

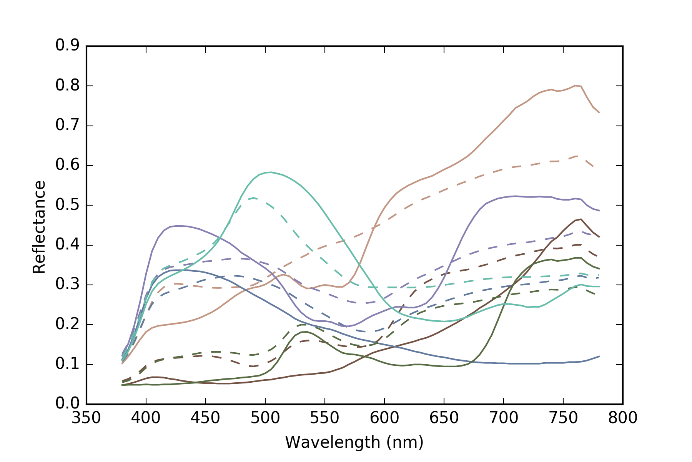Figure 8 The original reflectance spectra of the colors in the first row of MCC (solid lines) and their estimated ones by the proposed method with Neugebauer model (broken lines).

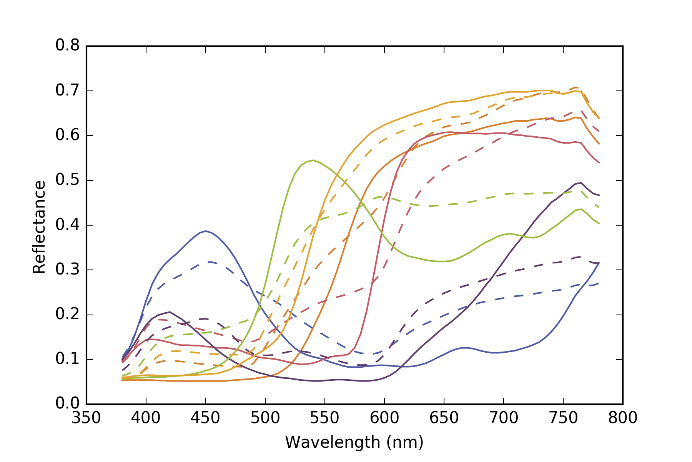Figure 9 The original reflectance spectra of the colors in the second row of MCC (solid lines) and their estimated ones by the proposed method with Neugebauer model (broken lines).

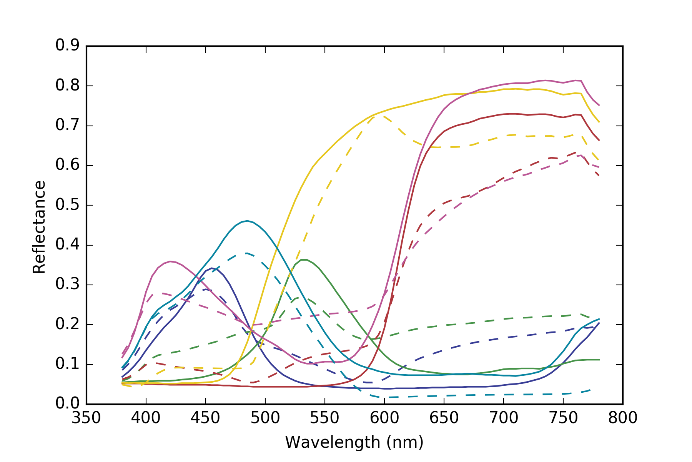Figure 10 The original reflectance spectra of the colors in the third row of MCC (solid lines) and their estimated ones by the proposed method with Neugebauer model (broken lines).

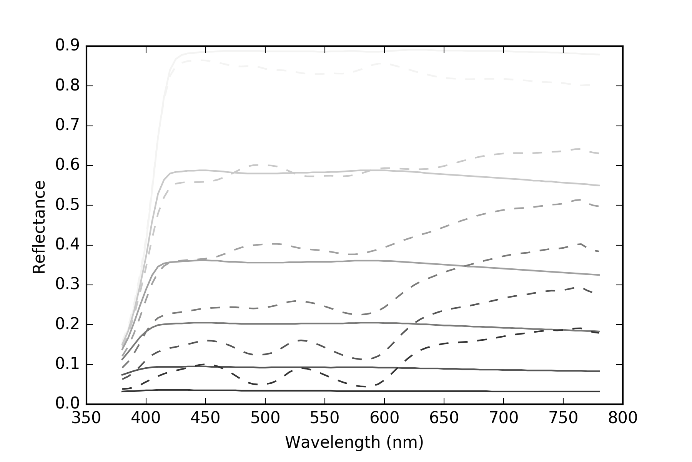Figure 11 The original reflectance spectra of the colors in the fourth row of MCC (solid lines) and their estimated ones by the proposed method with Neugebauer model (broken lines).

      On the other hand, from Figure 12 to Figure 15, we show the estimated reflectance spectra by the proposed method with sparse Neugebauer model, as well as Figures 8-11 with the Neugebauer model.

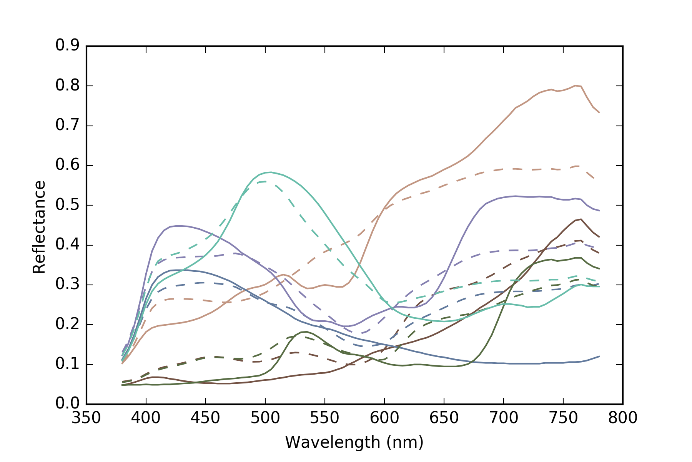Figure 12 The original reflectance spectra of the colors in the first row of MCC (solid lines) and their estimated ones by the proposed method with sparse Neugebauer model (broken lines).

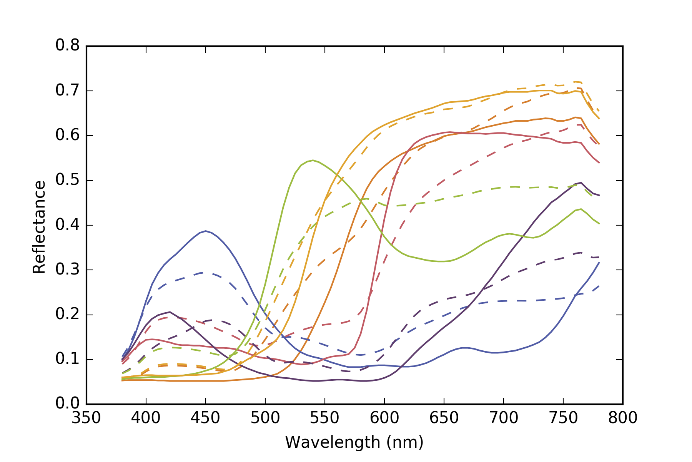Figure 13 The original reflectance spectra of the colors in the second row of MCC (solid lines) and their estimated ones by the proposed method with sparse Neugebauer model (broken lines).

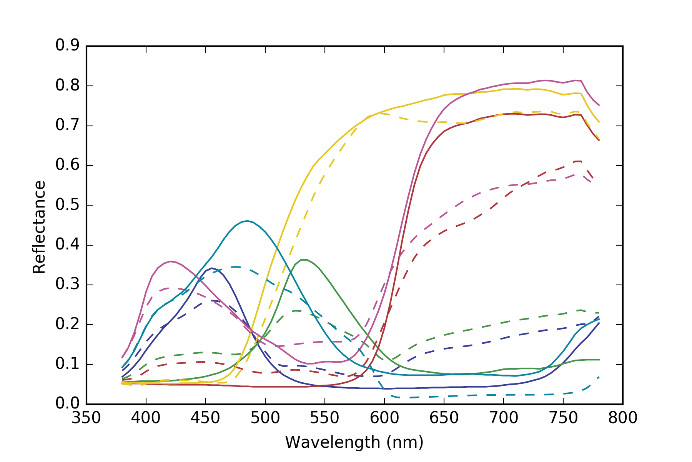Figure 14 The original reflectance spectra of the colors in the third row of MCC (solid lines) and their estimated ones by the proposed method with sparse Neugebauer model (broken lines).

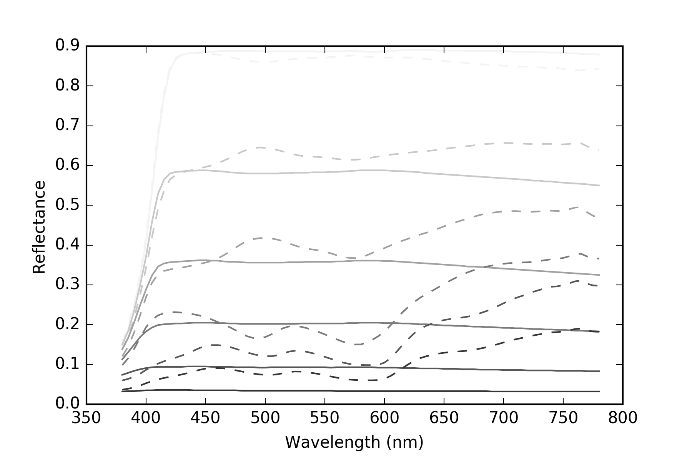Figure 15 The original reflectance spectra of the colors in the fourth row of MCC (solid lines) and their estimated ones by the proposed method with sparse Neugebauer model (broken lines).

      We evaluate the mean squared error between the original and estimated reflectance spectra given by

for the th color in MCC. Figure 16 shows the result where the vertical and horizontal axes denote the mean squared error and the identification number of MCC colors, respectively, and the blue and red bars denote the conventional nonsparse and the sparse Neugebauer models, respectively. In 18 colors among all 24 colors, the sparse Neugebauer model achieved smaller  than the conventional one. The average of  for  given by

are  for the conventional Neugebauer model and  for the sparse one.

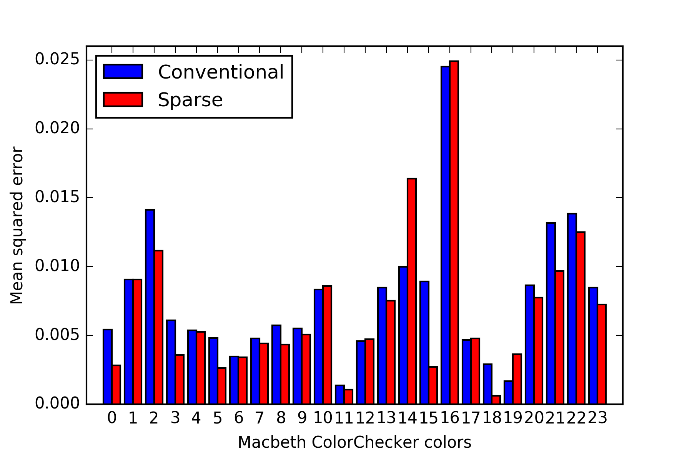Figure 16 Mean squared error of estimated reflectance spectra.

      Next, we also evaluate the same measure using the leave-one-out cross-validation [11], where the spectral reflectance of the th color in MCC is removed from  to evaluate . Figure 17 shows the result, where the sparse Neugebauer model (red bars) achieved smaller  in 15 colors among all 24 colors than the conventional Neugebauer model (blue bars). The values of  are  for the conventional Neugebauer model and  for the sparse one.

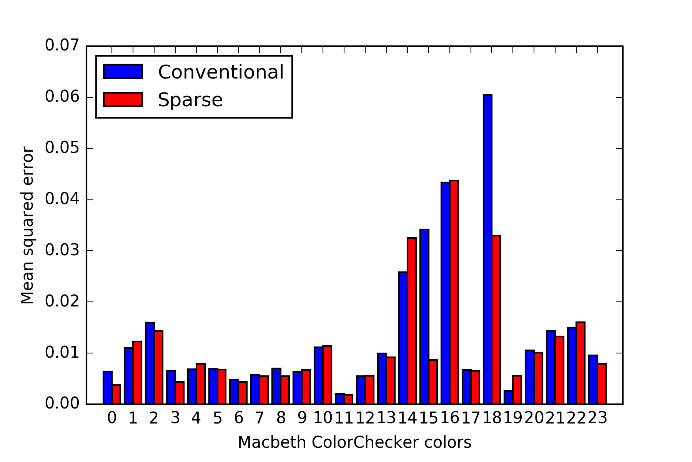Figure 17 Mean squared error of estimated reflectance spectra evaluated by the leave-one-out cross-validation.

      Finally, we show the results of color reproduction from the estimated reflectance spectra. Figure 18 shows the original Neugebauer primaries: red, green, blue, black, cyan, magenta, yellow and white.

Figure 18 Neugebauer primaries.

Figure 19 shows the reproduced Neugebauer primaries with the conventional Neugebauer model, in which blue is wrongly transformed into magenta.

Figure 19 Reproduced Neugebauer primaries from the estimated reflectance spectra with Neugebauer model.

On the other hand, the reproduced Neugebauer primaries with the sparse Neugebauer model is shown in Figure 20, where blue is correctly reproduced as well as the other colors.

Figure 20 Reproduced Neugebauer primaries from the estimated reflectance spectra with sparse Neugebauer model.

      Figures 21 and 22 show the reproduced MCC colors with the conventional and sparse Neugebauer models, respectively. The reproduced colors are similar to the original ones in Figure 1. Additionally, note that the proposed method can be applied to not only the CMYK-printed colors like MCC but also more general tristimulus values including material colors.

Figure 21 Reproduced MCC colors with Neugebauer model.

Figure 22 Reproduced MCC colors with sparse Neugebauer model.

      We evaluate the mean absolute error between the original and reproduced MCC colors given by

for the th color in MCC, where  and denote the reproduced sRGB values from the estimated reflectance spectra. Figure 23 shows the result, where the sparse Neugebauer model (red bars) achieved smaller  in 20 colors among all 24 colors than the conventional Neugebauer model. The average of  for  given by

are 17.65 for the conventional Neugebauer model and 13.81 for the sparse one.

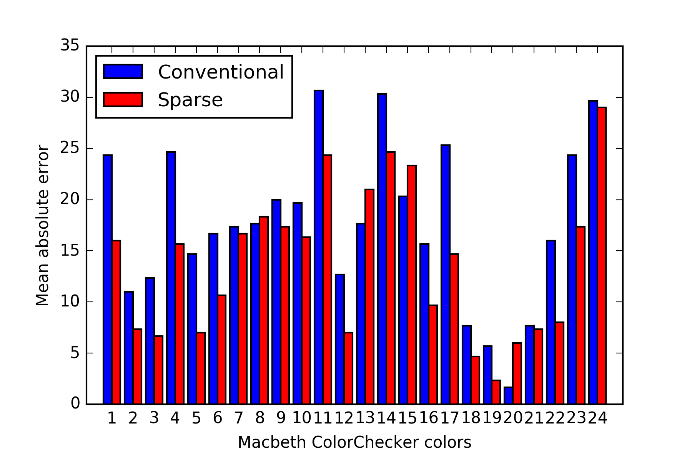Figure 23 Mean absolute error of reproduced MCC colors.

      Consequently, the sparse Neugebauer model improved the performance of both spectral reflectance estimation and color reproduction from the estimated spectral reflectance compared with the conventional Neugebauer model.

6.       Conclusion

      In this paper, we proposed a method for estimating spectral reflectance based on the Neugebauer model and its sparse version. The sparse Neugebauer model improved the estimation performance compared with the conventional Neugebauer model. We also proved the convergence property of the proposed algorithm for spectral reflectance estimation. Additionally, we reproduced the colors from the estimated spectral reflectance, in which the sparse Neugebauer model also improved the performance compared with the conventional one.

      For future work we would like to improve the performance of both spectral reflectance estimation and color reproduction by robustifying the proposed method, and compare the proposed method with other related methods including learning-based methods. We are also planning an application of the proposed method to the design of spectral reflectance for controlled color reproduction under various illuminations.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

This work was supported by JSPS KAKENHI Grant Number JP16H03019.

1. S. Westland, Computational Colour Science Using MATLAB, Wiley, 2004.
2. G. Sharma, S. Wang, “Spectrum recovery from colorimetric data for color reproductions,” in Proc. SPIE 4663, Color Imaging: Device-Independent Color, Color Hardcopy, and Applications VII, San Jose, CA, 2002.
3. T. Harifi, S. H. Amirshahi , F. Agahian, “Recovery of reflectance spectra from colorimetric data using principal component analysis embedded regression technique,” Opt. Rev., 15(6), 302–308, 2008.
4. M. M. Amiri, S. H. Amirshahi, “A step by step recovery of spectral data from colorimetric information,” J. Opt., 44(4), 373–383, 2015.
5. G. Wu, X. Shen, Z. Liu, S. Yang, M. Zhu, “Reflectance spectra recovery from tristimulus values by extraction of color feature match,” Opt. Quant. Electron., 48(1), 48:64, 2016.
6. V. Franc, V. Hlavá, M. Navara, “Sequential coordinate-wise algorithm for the non-negative least squares problem,” in Gagalowicz A., Philips W. (eds) Computer Analysis of Images and Patterns. CAIP 2005. Lecture Notes in Computer Science, vol 3691. Springer, Berlin, Heidelberg, 2005.
7. E. Reinhard, E. A. Khan, A. O. Akyuz, G. Johnson, Color Imaging: Fundamentals and Applications, A K Peters/CRC Press, 2008.
8. K. Inoue, K. Hara, K. Urahama, “Reflectance spectra recovery with non-negativity constraints,” in 2016 International Symposium on Intelligent Signal Processing and Communication Systems, Phuket, Thailand, 2016.
9. D. Shaked, N. Arad, , A. Fitzhugh, I. Sobel, “Color diffusion: Error-diffusion for color halftones,” HP Labs Technical Reports, HPL-96-128R1, 1999.
10. S. Boyd, L. Vandenberghe, Convex Optimization, Cambridge University Press, 2004.
11. S. Arlot, A. Celisse, “A survey of cross-validation procedures for model selection,” Statistics Surveys, 4, 40–79, 2010.

(Click to view)

(Click to view)