1            Introduction

The proliferation of access to information terminals, as well as the implementation of digital personal data transfers, requires the availability of means that ensure a reliable, fast and genuine exchange. In fact, the use of a communications network exposes the transfer of data to certain risks, which require adequate and appropriate security measures. For example, Pirated images can subsequently be the subject of data exchange and illegal digital storage. Data encryption is often the only effective way to meet these requirements. According to Shannon, the basic techniques [1] for an encryption system can be classified into two main categories: permutation of positions (diffusion) and transformation of values (confusion). And the combination between the two classes is also possible. In the literature, several algorithms based on confusion and diffusion have been developed [2-3]. Currently, the use of chaos in cryptosystems, has caught the attention of researchers. This is due to the characteristics of the chaotic signals. To quote, unpredictability, ergodicity, and sensitivity to parameters and initial values. Recently, several chaos-based articles have been proffered [4-5]. Unfortunately, the one-dimensional logistic map has been widely used in several cryptosystems based on chaos [6-7]. Nevertheless, this map has some disadvantages when it is used in cryptography such as not uniform distribution, small space key, chaotic discontinuous ranges, and periodicity in chaotic ranges [8]. Its very important to produce a new chaotic system with better chaotic performance. In this work, we proposed a method based on an improvement of the three chaotic maps, namely the Pseudorandomly Enhanced Logistics Map (PELM) [9], the Pseudorandomly Enhanced Sine Map (PESM) and the Pseudorandomly Enhanced Skew Tent Map (PESTM). Thus, the red channel of the original image is mixed with the ELM, the green channel with the ESM, and the blue channel with the ESTM. Then, a strong avalanche effect will be applied on the three mixed channels, so that a small perturbation on a pixel of the original image will be reflected on the entire image.

The paper is organized as follows. Section 2 makes a new chaotic maps by using the above mentioned three 1D chaotic maps. Section 3 gives a detailed explanation of the proposed image encryption scheme. Section 4 present experimental results demonstrating performance of the proposed method against statistical and sensitivity cryptanalysis. section 5 shows conclusion.

2          Thepseudorandomnumbergenerator

The proposed image encryption scheme relies on three improved chaotic maps PELM, PESME and the PESTM, for the generation of pseudo-random number sequences. In this section we show the improvement of the three chaotic maps in terms of chaotic behavior, Lyapunov exponent, bifurcation and distribution.

2.1         Pseudorandomly Enhanced Logistics Map

The logistic map is a simple dynamic nonlinear equation with a complex chaotic behavior, is one of the famous chaotic maps, expressed by the following equation:

                                 X_n+1 = µ × X_n × (1 − X_n)                            (1)

Where µ ∈ [0,4] is a control parameter of the logistic map, the variable X_n ∈ [0,1] with n is the iterations number used to generate the iterative values. The one-dimensional logistics map is characterized by its simple structure and its ease of implementation. Its usually used to encrypt large data in real time [11]. On the other hand, it has several weaknesses [10], including discontinuity, non-uniformity, short periodicity, numerical degradation and weak key space.

We have thus improved the pseudo-randomness of the sequences generated by the logistic map, by a simple multiplication by 10⁶ and an application of the modular arithmetic (mod 1). This new pseudorandom generator is indicated in equation (2) [9]:

X_n+1 = mod(((µ × X_n × (1 − X_n))(10⁶)) (2) where mod is the operation of module 1. the proposed generator has a Lyapunov exponent higher than that of the logistic map (Fig. 1), and a good distribution (Fig. 2).

2.2         Pseudorandomly Enhanced Sine Map

The sine map is also one of the one-dimensional chaotic maps whose chaotic behavior is similar to that of the logistic map described by the following equation:

                                   Y_n+1 = r ^× sin(π ^× Y_n)                              (3)

Where r ∈]0,1] is a control parameter of the sine map, the variable Y_n ∈ [0,1] with n is the iterations number used to generate the iterative values. We have also improved the pseudo-randomness of the sequences generated by the Sine map, by a simple multiplication by 10⁶ and an application of the modular arithmetic (mod 1). This new pseudo-random generator is indicated in equation (4):

                       Y_n+1 = mod(((r × sin(π × Y_n))(10⁶))                   (4)

To test the property of the PESM in terms of the Lyapunov exponent and distribution, several simulations and analysis were performed (see Fig. 1 and Fig.

2).

2.3         PseudorandomlyEnhancedSkewTent Map

The skew tent map is a one-dimensional simple chaotic system which can be described by [12]:

 Zbn if Zn < b    Zn+1 =   1−Zn if Zn > b   1−b

Zn ∈ [0,1]

(5)

Where Z_n ∈ [0,1] is the state of the chaotic system, and b ∈ [0,0.5] ∪ [0.5,1] is the control parameter. We have also improved the pseudo-randomness of the sequences generated by the skew tent map. This new pseudo-random generator is indicated in equation (6):

^ ^Zn)(10⁶)),1) if Z_n < b mod((( _b



Z_n+1 = ^_                                                                    Z_n ^∈ [0,1]

^ mod(((¹1⁻−^Zbⁿ)(10⁶)),1) if Z_n > b

(6)

The figure below shows the Lyapunov exponents of the logistic map, the sin map, the skew tent map, and of the pseudo-random generators proposed.

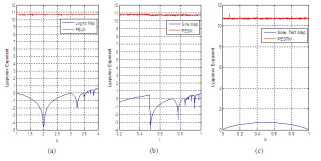Fig. 1 : Lyapunov exponent of: (a) Logistic Map and PELM; (b) Sine Map and PESM; (c) Skew Tent Map and PESTM.

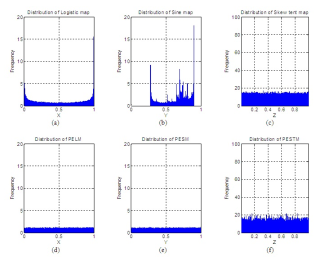Fig. 2: Distribution of: (a) Logistic Map; (b) Sine Map; (c) Skew Tent Map; (d) PELM; (e) PESM; (f) PESTM.

We can see in the fig. 1 that the Lyapunov exponent is large for the proposed pseudo-random generator. Therefore, this generator presents a higher and faster divergence between two chaotic trajectories having very similar initial conditions. From a cryptographic point of view, a good pseudo-random generator must produce chaotic sequences with uniform distribution. The figure below shows the distribution densities of the logistic map, the sin map, the skew tent map, and of the pseudo-random generators proposed.

It is clear from the fig. 2 that the pseudo-random generators proposed has a uniform distribution density. Therefore, has excellent statistical properties, and is more recommended to use for a robust encryption system.

3          Description of the proposed scheme

Our algorithm is based on three stages of confusion and a diffusion step. Let us consider an H × W color image P to be encrypted. With H is the height and W the width. The process of our proposed algorithm will be summarized in Fig. 3 :

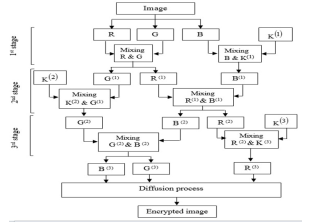Fig. 3: Flowchart of the proposed algorithm

3.1         Confusion process

The confusion step is described as follows :

Step 1: Load the plain image P of size W × H, and divide it into 3 images with R, G and B channels respectively.

Step 2: Choose six values X₀,Y₀,Z₀,µ,r and b which represent the initial conditions and the control parameters of the pseudo-random generators proposed. Step 3 : Iterate the PELM, PESM and PESTM respectively for W × H times to get the state X =

^{X₀,X₁,…,X_W×H−₁^}, Y = ^{X₀,Y₁,…,Y_W×H−₁^} and Z =

^{Z₀,Z₁,…,Z_W×H−₁^}.

Step 4 : Generate three keys K⁽¹⁾, K⁽²⁾ and K⁽³⁾. With K⁽¹⁾ = mod(f loor(X(i) × 10¹⁴),256), K⁽²⁾ = mod(f loor(Y(i) × 10¹⁴),256), and K⁽³⁾ = mod(f loor(Z(i)×10¹⁴),256), With i = 0, 1 … W ×H −1. Then convert each key into a matrix of dimensions with the size of W × H.

Step 5: Create three invertible matrices M⁽¹⁾, M⁽²⁾ and M⁽³⁾ used for iterative mixing. With

                                                !                                            !

M(1) ₌ 1 p1 _{, M}(2) ₌ 1 p2 _, q1 1+p1q1 q2 1+p2q2

                                                                              !

                             and M(3) ₌       1    p3

q3 1+p3q3

Where p₁ and q₁ are from K⁽¹⁾ , p₂ and q₂ are from K⁽²⁾, p₃ and q₃ are from K⁽³⁾.

Step 6 : Mix each color channel with to another or with a key according to the following formulas :

R (1) ! = M(1) × R ! (mod 256) G(1)                                        G	(7)
B (1)                                      ! = M(1) × B(1) ! (mod 256) T mp(1)                                         K	(8)
R (2) ! = M(2) × R ! (mod 256) G(2)                                        G	(9)
G (2)                              ! = M(2) × G(1)(2) ! (mod 256) T mp(2)                                                K	(10)
B (3) ! = M(3) × B(2)(2) ! (mod 256) G(3)                                         G	(11)
R (3)                              ! = M(3) × R(2)(3) ! (mod 256) T mp(3)                                                K	(12)

T mp⁽¹⁾, T mp⁽²⁾ and T mp⁽³⁾ are variables not taken into consideration in the encryption process.

3.2         Diffusion process

The diffusion step is described as follows :

Step 1: Convert R⁽³⁾, G⁽³⁾ and B⁽³⁾ to a vectors of size W × H , and concatenate them into a single vector V ^(RGB) =

^{r0,r1,…,rW×H−1,g0,g1,…,gW×H−1,b0,b1,…,bW×H−1^}.

Where ^{r₀,r₁,…,r_W×H−₁^}, ^{g₀,g₁,…,g_W×H−₁^} and {b₀,b₁,…,b_W×_H−₁} are respectively the components of R(3), G(3) and B(3).

Step 2 : Concatenate the three sequences X, Y and Z into a single vector V ^(K) =

^{X₀,X₁,…,X_W×H−1,Y₀,Y₁,…,Y_W×H−1,Z₀,Z₁,…,Z_W×H−₁^}.

Then by sorting the order of the vector V ^(K), the chaotic sequence is changed into a sorted order. This sequence is called V ^(p).

Step 3 :                     Obtain the permuted image pixel vector

0

P = {p₀,p₁,…,p_W×_H−₁}, by using the permutation position vector V ^(p) according to the following formula

:

                                   P (i) = V ^(RGB)(V ^(p)(i))                              (13)

Step        4              :               Obtain    the          diffusion vector    D             = {d₀,d₁,…,d₃×W×H−₁}, by the following algorithm :

Algorithm 1: Diffusion mechanism S ←− 0 //Initialisation

For i ←− 0 T o 3 × W × H − 1

0

S ←− mod(S +P (i),256)

EndFor D(0) ←− S For i ←− 1 T o 3 × W × H − 1

0

S ←− D(i − 1) ⊕ P (i)

D(i) ←− S ⊕ V (p)(i)

EndFor

Step 5 : Convert the diffusion vector D into the R, G and B color image with the size of W ⊗ H.

3.3         Decryption algorithm

The decryption process is similar to that of encryption procedure in the reversed order.

4          Experimental results and analysis

In this section, we will validate our encryption system in terms of key space, histogram, entropy, correlation coefficient, NPCR, and UACI. All simulations are performed on a personal computer. Table 1 shows the hardware, the software environment and the image source.

Table. 1: Specification table

Processor	Intel CoreTM i5-2430M CPU 2.4GHZ
RAM	4GB
Operating system	Windows 8 professional
Programming language	JAVA
Image source	USC-SIPI image data base [13]

4.1         Space of key

The exhaustive attack is to try all possible combinations of keys until obtaining a clear text. Therefore, in a good image cryptosystem, the space of key should be large enough to make brute-force attack infeasible. The secret key of the proposed cryptosystem contains six real numbers (µ, r, b , X₀, Y₀, Z₀). If the precision is 10⁻¹⁴, the key space size can reach to 2²⁵². From a cryptographic point of view, the size of the key space should not be less than 2¹⁰⁰ to ensure a high level of Security [14]. This means that our algorithm can withstand the brute force attack.

4.2         Statistical Analysis

4.2.1        Histogram analysis

An image histogram is a graphical representation of the number of pixels with the same gray level. Thus, the abscissa axis represents the color level, which starts from zero (color channel off) to 255 (maximum color channel). Fig. 4(a)-(b) show the plain and cipher image. Fig. 4(c)-(d) show the histogram of plain and cipher components’ R, G, and B.

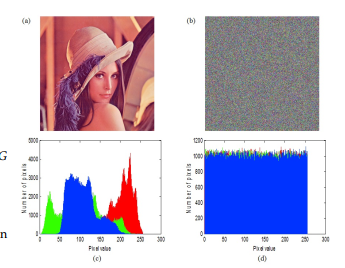Fig. 4: (a) Lena 512×512; (b)encrypted image; (c) Histogram of plain-image; (d) Histogram of encrypted image

Comparing the two histograms of plain and cipher image, we can see that histogram of encrypted image is fairly uniform and is significantly different from that of the original image, and that the encrypted images obtained do not provide any information to the attacker, which can strongly resist statistical attacks.

4.2.2        Information Entropy

Information entropy is designed to evaluate the uncertainty in a random variable as shown in the following equation [1]:

M

X

                          H(m) = −          P (m_i)log(P (m_i))                  (14)

i=0

Where, M is the total number of symbols and represents the probability of occurrence of the symbol, for a grayscale image with a data range of, its maximum Information entropy is 8. The results are shown in Table 2.

Table. 2: Entropy of the original image and the encrypted image

mages	Original	Encrypted
House 256 × 256	7.068625	7.999159
Lena 512 × 512	7.750197	7.999779
Peppers 512 × 512	7.669825	7.999776

It is clear from Table 2 that the values of the entropy of the encrypted images are very close to the theoretical value (which is equal to 8).

4.2.3        Correlation analysis

The obvious characteristics of visually meaningful images is redundancy and strong correlation among adjacent pixels, and it can be used by attackers. In order to test the correlation, we randomly select 1000 pairs of adjacent pixels in three dimension (vertical, horizontal and diagonal). The results are shown in Table 3 and Fig 5.

The correlation coefficient for a sequence of adjacent pixels is given by the following formula:

cov(u,v)

                                 ruv = p p                               ,       (15)

                                                 D(u)      D(v)

Where u and v represent two vectors formed respectively by the values of the pixels of the chosen sequence of the image and the values of their adjacent pixels. The terms cov(u,v), D(u) and D(v) are calculated by the following formulas:

N

1 X

E(u) =       ui, N i=1	(16)
N 1 D(u) =        X[ui − E(u)]2,	(17)

N

i=1

N

1 X

            Cov(u,v) =             [u_i − E(u)] ∗ [v_i − E(v)]             (18)

N

i=1

Where N is a large number of adjacent pixel pairs randomly selected in the image (In our case N = 1000), u_i and v_i are respectively the color levels of the collected pixels.

Table. 3: Correlation coefficient of the two adjacent pixels for the original and encrypted image

We can see in the Table 3, the correlation coefficient values are nearing to zero and negative values which prove that there is no correlation between the plain and cipher image.

4.3         Differential analysis

The Number of Pixels Change Rate (NPCR) [15] and Unified Average Changing Intensity (UACI) [16] are used to analyze the effect of slight change (one bit of single pixel) in the plain image on the cipher image [21]. The formulas used to calculate NPCR and UACI are defined by the following two equations:

Pi,j g(i,j)

                             NP CR =    × 100

W ^× H

             UACI = 100 ^{X |}C1(i,j) ⁻ C2(i,j)^| _× 100

                             W × H               

i,j

Where, C₁(i,j) is the encrypted image and C₂(i,j) is the encrypted image after changing a pixel of the clear image. For the pixels at the position (i,j) , if C₁(i,j) , C₂(i,j) , then g(i,j) = 1 , otherwise it’s equal to zero.

A value of UACI > 33.4635% and NP CR > 99.6094% ensures that an image encryption scheme is immune to a differential attack. Table 4 below shows the results of the UACI and NPCR simulations.

Table. 4: NPCR and UACI values after changing the value of a pixel.

It is clear from Table 4 that the value of NPCR is greater than 99.6094% and that of UACI is greater than 33.4635%. That is to say a modification of a single pixel of the original image results in a radical change of all the pixels of the encrypted image.

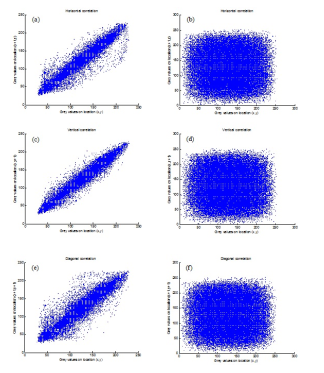Fig. 5: Correlation distribution of adjacent pixels of the Lena 512 × 512 in directions, (a) Horizontal, (c) Vertical, (e) diagonal. Correlation distribution of adjacent pixels of the Lena 512 × 512 encrypted in the directions, (b) Horizontal, (d) Vertical, (f) diagonal.

5          Conclusion

In this work, firstly, we proposed a technique of making an effective pseudorandom number generator by using a difference of the output states of three famous one-dimension chaotic maps namely logistic map, sine map and skew tent map. Simulations evaluations in terms of the Lyapunov exponent and the

distribution density showed that the proposed generator is able to generate a one-dimension chaotic system with excellent statistical properties and good chaotic behavior. Secondly, we proposed a novel algorithm based on an iterative mixing of the three components R, G and B with the three chaotic sequences generated from the proposed pseudo-random generator, followed by a strong diffusion. The values of the performance metrics in terms of key space, histogram, entropy, correlation coefficient, NPCR, and UACI, satisfy that the proposed algorithm is extremely difficult to break and withstands on various kinds of security attacks.

1. Shannon, C. E. (1949). Communication theory of secrecy systems. Bell Labs Technical Journal, 28(4), 656-715.
2. Chen, G., Mao, Y., and Chui, C. K. (2004). A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos, Solitons and Fractals, 21(3), 749-761.
3. Kanso, A., and Ghebleh, M. (2012). A novel image encryption algorithm based on a 3D chaotic map. Communications in Nonlinear Science and Numerical Simulation, 17(7),2943-2959.
4. Liu, L., Zhang, Q., and Wei, X. (2012). A RGB image encryption algorithm based on DNA encoding and chaos map. Computers and Electrical Engineering, 38(5), 1240-1248.
5. Hua, Z., and Zhou, Y. (2016). Image encryption using 2D Logistic-Adjusted-Sine map. Information Sciences, 339, 237-253.
6. Wong, K. W., Kwok, B. S. H., and Law, W. S. (2008). A fast image encryption scheme based on chaotic standard map. Physics Letters A, 372(15), 2645-2652.
7. Hanchinamani, G., and Kulakarni, L. (2014). A New Approach for Image Encryption Based on Cyclic Rotations and Multiple Blockwise Diffusions Using Pomeau-Manneville and Sin Maps. JCSE, 8(4), 187-198.
8. Arroyo, D., Alvarez, G., and Fernandez, V. (2008). On the inadequacy of the logistic map for cryptographic applications. arXiv preprint arXiv:0805.4355.
9. Murillo-Escobar, M. A., Cruz-Hernndez, C., Cardoza- Avendao, L., and Mndez-Ramrez, R. (2017). A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dynamics, 87(1), 407-425.
10. Arroyo, D., Alvarez, G., and Fernandez, V. (2008). On the inadequacy of the logistic map for cryptographic applications. arXiv preprint arXiv:0805.4355.
11. Mazloom, S., and Eftekhari-Moghadam, A. M. (2009). Color image encryption based on coupled nonlinear chaotic map. Chaos, Solitons and Fractals, 42(3), 1745-1754.
12. Lai, D., Chen, G., and Hasler, M. (1999). Distribution of the Lyapunov exponent of the chaotic skew tent map. International Journal of Bifurcation and Chaos, 9(10), 2059-2067.
13. http://sipi.usc.edu/database/database.php?
14. Alvarez, G., and Li, S. (2006). Some basic cryptographic requirements for chaos-based cryptosystems. International Journal of Bifurcation and Chaos, 16(08), 2129-2151.
15. Akhshani, A., Behnia, S., Akhavan, A., Hassan, H. A., and Hassan, Z. (2010). A novel scheme for image encryption based on 2D piecewise chaotic maps. Optics Communications, 283(17), 3259-3266.
16. Kwok, H. S., and Tang,W. K. (2007). A fast image encryption system based on chaotic maps with finite precision representation. Chaos, solitons and fractals, 32(4), 1518-1529

(Click to view)

(Click to view)