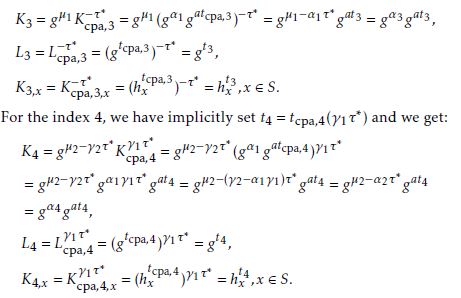1 Introduction

Access control is one of the fundamental processes and requirements in cybersecurity. Attribute-based encryption (ABE) invented by Sahai and Waters [1], where attributes mean authorized credentials, enables to realize access control which is functionally close to role-based access control (RBAC), but by encryption. In key-policy ABE (KP-ABE) introduced by the subsequent work of Goyal, Pandey, Sahai and Waters [2], a secret key is associated with an access policy over attributes, while a ciphertext is associated with a set of attributes. In a dual manner, in ciphertext-policy ABE (CP-ABE) [2, 3, 4], a ciphertext is associated with an access policy over attributes, while a secret key is associated with a set of attributes. In a KP-ABE or CP-ABE scheme, a secret key works to decrypt a ciphertext if and only if the associated set of attributes satisfies the associated access policy. The remarkable feature of ABE is attribute privacy; that is, in decryption, no information about the access policy and the identity of the secret key owner in the case of KPABE (or, the attributes and the identity of the secret key owner in the case of CP-ABE) leaks except the fact that the set of attributes satisfies the access policy. Since the proposals, it has been studied to attain certain properties such as indistinguishability against chosen-plaintext attacks (IND-CPA) in the standard model [4] and adaptive security against adversary’s choice of a target access policy [5].

In this paper¹, we work through resolving a problem of constructing a shorter ABE scheme that attains indistinguishability against chosen-ciphertext attacks (IND-CCA) in the standard model. Here CCA means that an adversary can collects decryption results of ciphertexts of its choice through adversaries’ attacking. Note that “provable security” of a cryptographic primitive is now a must requirement when we employ the primitive in a system, where it means that an appropriately defined security is polynomially reduced to the hardness of a computational problem. Moreover, the CCA security of an encryption scheme is preferable to attain because the CCA security is one of the theoretically highest securities and hence the scheme can be used widely.

To capture the idea of our approach, let us recall the case of identity-based encryption (IBE). The CHK transformation of Canetti, Halevi and Katz [7] is a generic tool for obtaining IND-CCA secure IBE scheme. It transforms any hierarchical IBE (HIBE) scheme that is selective-ID IND-CPA secure [8] into an IBE scheme that is adaptive-ID IND-CCA secure [8]. A point of the CHK transformation is that it introduces a dummy identity vk that is a verification key of a one-time signature. Then a ciphertext is attached with vk and a signature σ, which is generated each time one executes encryption. In contrast, the direct chosen-ciphertext security technique for IBE of Boyen, Mei and Waters [9] is individual modification for obtaining an IND-CCA secure IBE scheme. It converts a HIBE scheme that is adaptive-ID IND-CPA secure into an IBE scheme that is adaptive-ID INDCCA secure. Though the technique needs to treat each scheme individually, the obtained scheme attains better performance than that obtained by the generic tool (the CHK transformation). Let us transfer into the case of ABE. The transformation in [10] is a generic tool for obtaining IND-CCA secure ABE scheme. It transforms any ABE scheme (with the delegatability or the verifiability [10]) that is IND-CPA secure into an ABE scheme that is IND-CCA secure. A point of their transformation is, similar to the case of IBE, that it introduces a dummy attribute vk that is a verification key of a one-time signature. Then a ciphertext is attached with vk and a signature σ. Notice here that discussing direct chosen-ciphertext security modification for ABE (in the standard model) is a missing piece. One of the reasons seems that there is an obstacle that a Diffie Hellman tuple to be verified is in the target group of a bilinear map. In that situation, the bilinear map looks of no use.

1.1       Our Contribution

A contribution is that we fill in the missing piece; we demonstrate direct chosen-ciphertext security modification in the case of the Waters CP-ABE scheme [4] and the KP-ABE scheme of Ostrovsky, Sahai and Waters [11] To overcome the above obstacle, we employ the technique of the Twin Diffie-Hellman Trapdoor Test of Cash, Kiltz and Shoup [12]. In addition, we also utilize the algebraic trick of Boneh and Boyen [13] and Kiltz [14] to reply for adversary’s decryption queries.

1.2      Related Works

Waters [4] pointed out that IND-CCA security would be attained by the CHK transformation. Gorantla, Boyd and Nieto [15] constructed a IND-CCA secure CP-ABKEM in the random oracle model. In [10] the authors proposed a generic transformation of a INDCPA secure ABE scheme into a IND-CCA secure ABE scheme. Their transformation is considered to be an ABE-version of the CHK transformation, and it is versatile. Especially, it can be applied to non-pairingbased scheme.

The Waters CP-ABE [4] can be captured as a CP-ABKEM: the blinding factor can be considered as a random one-time key. This Waters CP-ABKEM is IND-CPA secure because the Waters CP-ABE is proved to be IND-CPA secure. For theoretical simplicity, we demonstrate an individual conversion of the Waters CP-ABKEM into a CP-ABKEM which is IND-CCA secure. Then we provide a CP-ABE scheme which is IND-CCA secure. As for KP-ABE, we demonstrate an individual conversion of KP-ABKEM of Ostrovsky, Sahai and Waters [11], which is IND-CPA secure, into a KP-ABKEM which is IND-CCA secure. Then we provide a KP-ABE scheme which is IND-CCA secure.

Finally, we note that there is a remarkable work of CP-ABE schemes and KP-ABE schemes with constantsize ciphertexts [16, 17]. Our direct chosen-ciphertext security modification is not constant-size ciphertexts but a different approach for easier implementation in engineering.

1.3 Organization of the Paper

In Section 2, we survey concepts, definitions and techniques needed. In Section 3, we revisit the concept, the algorithm and the security of the twin Diffie Hellman technique. In Section 4, we construct a CCAsecure CP-ABKEM from the Waters CPA-secure CPABKEM [4], and provide a security proof. Also, we describe the encryption version, a CCA-secure CPABE. In Section 5, we construct a CCA-secure KP-ABKEM from the Ostrovsky-Sahai-Waters CPA-secure KP-ABKEM [11], and provide a security proof. Also, we describe the encryption version, a CCA-secure KPABE. In Section 6, we compare efficiency of our CP-ABE and KP-ABE schemes with the original schemes, and also, with the schemes obtained by applying the generic transformation [10] to the original schemes. In Section 7, we conclude our work.

2 Preliminaries

The security parameter is denoted λ. A prime of bit length λ is denoted p. A multiplicative cyclic group of order p is denoted G. The ring of exponent domain of G, which consists of integers from 0 to p − 1 with modulo p operation, is denoted Z_p.

2.1 Bilinear Map

We remark first that our description in the subsequent sections is in the setting of a symmetric bilinear map for simplicity, but we can employ an asymmetric bilinear map instead for better efficiency as is noted in Section 6. Let G and G_T be two multiplicative cyclic groups of prime order p. Let g be a generator of G and e be a bilinear map, e : G × _G → _GT . The bilinear map e has the following properties:

1. Bilinearity: for all u,v ∈ _G and a,b ∈ _Zp, we have e(u^a,v^b) = e(u,v)^ab.
2. Non-degeneracy: e(g,g) , id_GT (: the identity element of the group G_T ).

Parameters of a bilinear map are generated by a probabilistic polynomial time (PPT) algorithm Grp on input λ: (p,G,GT ,g,e) ← Grp(λ).

Hereafter we assume that the group operation in G and GT and the bilinear map e : G ^× G ^→ GT are computable in PT in λ.

2.2 Access Structure

Let U = {χ₁,…,χ_u} be a set of attributes, or simply set U = {1,…,u} by numbering. An access structure, which corresponds to an access policy, is defined as a collection A of non-empty subsets of U; that is, A ⊂ 2^U \{φ}. An access structure A is called monotone if for any B ∈ _A and B ⊂ C, C ∈ _A holds. The sets in A are called authorized sets, and the sets not in A are called unauthorized sets. We will consider in this paper only monotone access structures.

2.3 Linear Secret-Sharing Scheme

We only describe a linear secret-sharing scheme (LSSS) in our context of attribute-based schemes. A secret-sharing scheme Π over the attribute universe U is called linear over Z_p if:

1. The shares for each attribute form a vector over Z_p, 2. There exists a matrix M of size l×n called the share generating matrix for Π and a function ρ which maps each row index i of M to an attribute in U = {1,…,u}: ρ : ^{1,…,l^{} → U}.

To make shares, we first choose a random vector v~ = (s,y₂,…,y_n) ∈ _Zⁿ_p: s is a secret to be shared. For i = 1 to l, we calculate each share λ_i = v~·M_i, where M_i denotes the i-th row vector of M and · denotes the formal inner product. LSSS Π = (M,ρ) defines an access structure A through ρ.

Suppose that an attribute set S satisfies A (S ∈ _A) and let I_S = ρ⁻¹(S) ⊂ {1,…,l}. Then, let {ω_i ∈ _Zp;i ∈ I_S} be a set of constants (linear reconstruction constants) such that if {λ_i ∈ _Zp;i ∈ I_S} are valid shares of a secret s according to M, then ^P_i∈_IS ω_iλ_i = s. It is known that these constants {ω_i}_i∈_IS can be found in time polynomial in l: the row size of the share-generating matrix M. If S does not satisfy A (S <A), then no such constants {ω_i}_i∈I_S exist.

2.4    Attribute-Based Key Encapsulation Mechanism

Ciphertext-policy attribute-based key encapsulation mechanism (CP-ABKEM). A CP-ABKEM consists of four PPT algorithms (Setup, Encap, KeyGen, Decap)^[1].

Setup(λ,U). A setup algorithm Setup takes as input the security parameter λ and the attribute universe U = {1,…,u}. It returns a public key PK and a master secret key MSK.

Encap(PK,A). An encapsulation algorithm Encap takes as input the public key PK and an access structure A. It returns a random string κ and its encapsulation ψ. Note that A is contained in ψ. KeyGen(PK,MSK,S). A key generation algorithm KeyGen takes as input the public key PK, the master secret key MSK and an attribute set S. It returns a secret key SK_S corresponding to S. Note that S is contained in SK_S.

Decap(PK,SK_S,ψ). A decapsulation algorithm Decap takes as input the public key PK, an encapsulation (we also call it a ciphertext according to context) ψ and a secret key SK_S. It first checks whether S ∈ _A, where S and A are contained in SK_S and ψ, respectively. If the check result is False, it puts κˆ =⊥. It returns a decapsulation result κˆ.

Chosen-Ciphertext Attack on CP-ABKEM. According to previous works (for example, see [15]), the chosen-ciphertext attack on a CP-ABKEM is formally defined as the indistinguishability game (IND-CCA game). In this paper, we consider the selective game on a target access structure (IND-sel-CCA game); that is, the adversary A declares a target access structure∗

A before A receives a public key PK, which is defined as the following experiment.

Experimentind-sel-ccaA_,CP-ABKEM(λ,U)∗

A ← A(λ,U),(PK,MSK) ← Setup(λ,U)

 _{← A}KeyGen(PK,MSK,·),Decap(PK,SK_·,·)(PK)

(κ^∗,ψ^∗) ← Encap(PK,A^∗),κ ← KeySp(λ),b ← {0,1} If b = 1 then κ˜ = κ^∗ else κ˜ = κ

         _b0 _{← A}KeyGen(PK,MSK,·),Decap(PK,SK_·,·)(κ,ψ_˜     ∗)

If b⁰ = b then return ^Win else return ^Lose.

In the above experiment, two kinds of queries are issued by A. One is key-extraction queries. Indicating an attribute set S_i, A queries its key-extraction oracle KeyGen(PK,MSK,·) for the secret key SK_Si . Here we do not require any input attribute sets S_i1 and S_i2 to be distinct. Another is decapsulation queries. Indicating a pair (S_j,ψ_j) of an attribute set and an encapsulation, A queries its decapsulation oracle Decap(PK, SK_·,·) for the decapsulation result κˆ_j. Here an access structure A_j, which is used to generate an encapsulation ψ_j, is implicitly included in ψ_j. In the case that S <A, κˆ_j =⊥ is replied to A. Both kinds of queries are at most q_k and q_d times in total, respectively, which are polynomial in λ.

The access structure A^∗ declared by A is called a target access structure. Two restrictions are imposed on A concerning A^∗. In key-extraction queries, each attribute set S_i must satisfy S_i <A^∗. In decapsulation queries, each pair (S_j,ψ_j) must satisfy S_j <A^∗ ∨ ψ_j , ψ∗.

The advantage of the adversary A over CP-ABKEM in the IND-CCA game is defined as the following probability:

Advind-sel-ccaA,CP-ABKEM(λ,U) def= Pr[Experimentind-sel-cca_A,CP-ABKEM(λ,U) returns Win].

CP-ABKEM is called selectively secure against chosenciphertext attacks if, for any PPT adversary A and for any attribute universe U, Adv^ind-sel-cca_A,CP-ABKEM(λ,U) is negligible in λ. Here we must distinguish the two cases; the case that U is small (i.e. |U| = u is bounded by a polynomial of λ) and the case that U is large (i.e. u is not necessarily bounded by a polynomial of λ). We assume the small case in this paper.

In the indistinguishability game against chosenplaintext attack (IND-CPA game), the adversary A issues no decapsulation query (that is, q_d = 0).

Ciphertext-Policy Attribute-Based Encryption Scheme (CP-ABE). In the case of the encryption version (i.e. CP-ABE), Encap(PK,A) and Decap(PK,SK_S,ψ) are replaced by PPT algorithms Encrypt(PK,A,m) and Decrypt(PK,SK_S,CT), respectively, where m and CT mean a message and a ciphertext, respectively.

The IND-CCA game for CP-ABE is defined in the same way as for CP-ABKEM above, except the following difference. In Challenge phase, the adversary A submits two equal length messages (plaintexts) m₀ and m₁. Then the challenger flips a coin b ∈ {0,1} and gives an encryption result CT of m_b to A. In Guess phase, the adversary A returns b⁰ ∈ {0,1}. If b⁰ = b, then A wins in the IND-CCA game. Otherwise, A loses.

Key-Policy         Attribute-Based       Key        Encapsulation

Mechanism (KP-ABKEM) and Encryption Scheme (KP-ABE). The key-policy case is analogously defined as the case of the ciphertext-policy case. We state only the syntax and the security experiment of the key-policy ABKEM.

Setup(λ,U). A setup algorithm Setup takes as input the security parameter λ and the attribute universe U = {1,…,u}. It returns a public key PK and a master secret key MSK.

Encap(PK,S). An encapsulation algorithm Encap takes as input the public key PK and an attribute set S. It returns a random string κ and its encapsulation ψ. Note that S is contained in ψ.

KeyGen(PK,MSK,A). A key generation algorithm KeyGen takes as input the public key PK, the master secret key MSK and an access structure A. It returns a secret key SK_A corresponding to S. Note that A is contained in SK_A.

Decap(PK,SK_A,ψ). A decapsulation algorithm Decap takes as input the public key PK, an encapsulation (we also call it a ciphertext according to context) ψ and a secret key SK_A. It first checks whether S ∈ _A. If the check result is False, it puts κˆ =⊥. It returns a decapsulation result κˆ.

Chosen-Ciphertext Attack on KP-ABKEM. The selective game on a target attribute set (IND-sel-CCA game) is defined by the following experiment.

Experimentind-sel-ccaA_,KP-ABKEM(λ,U)

S^∗ ← A(λ,U),(PK,MSK) ← Setup(λ,U)

 _{← A}KeyGen(PK,MSK,·),Decap(PK,SK_·,·)(PK)

(κ^∗,ψ^∗) ← Encap(PK,S^∗),κ ← KeySp(λ),b ← {0,1} If b = 1 then κ˜ = κ^∗ else κ˜ = κ

          _b0 _{← A}KeyGen(PK,MSK,·),Decap(PK,SK_·,·)(κ,ψ_˜    ∗)

If b⁰ = b then return ^Win else return ^Lose.

2.5    Target Collision Resistant Hash Functions

Target collision resistant (TCR) hash functions [18] are treated as a family. Let us denote a function family as Hfam(λ) = {H_µ}_µ∈_HKey(λ₎. Here HKey(λ) is a hash key space, µ ∈ HKey(λ) is a hash key and H_µ is a function from {0,1}^∗ to {0,1}^λ. We may assume that H_µ is from {0,1}^∗ to Z_p, where p is a prime of length λ.

Given a PPT algorithm CF , a collision finder, we consider the following experiment (the target collision resistance game).

ExperimenttcrCF ,Hfam(λ)

m^∗ ← CF (λ),µ ← HKey(λ),m ← CF (µ)

If m^∗ , m ∧ H_µ(m^∗) = H_µ(m) then return ^Win else return ^Lose.

Then we define CF ’s advantage over Hfam in the game of target collision resistance as follows.

AdvtcrCF ,Hfam(λ)

def= Pr[Experimenttcr_{CF ,Hfam}(λ) returns Win].

We say that Hfam is a TCR function family if, for any

PPT algorithm CF , Adv^tcr_CF ,_Hfam(λ) is negligible in λ.

TCR hash function families can be constructed based on the existence of a one-way function [18].

3 The Twin Diffie-Hellman Technique Revisited

A 6-tuple (g,X₁,X₂,Y,Z₁,Z₂) ∈ G⁶ is called a twin Diffie-Hellman tuple if the tuple is written as (g,g^x1,g^x2,g^y,g^x1y,g^x2y) for some elements x₁,x₂,y in

Z_p. In other words, a 6-tuple (g,X₁,X₂,Y,Z₁,Z₂) is a twin Diffie-Hellman tuple (twin DH tuple, for short) if Y = g^y and Z₁ = X₁^y and Z₂ = X₂^y.

The following lemma of Cash, Kiltz and Shoup will be used in the security proof to decide whether a tuple is a twin DH tuple or not.

Lemma 1 (“Trapdoor Test”[12]) Let X₁,r,s be mutually independent random variables, where X₁ takes values in G, and each of r,s is uniformly distributed over Z_p. Define the random variable X₂ = X₁^−rg^s. Suppose that Y,ˆ Zˆ₁,Zˆ₂ are random variables taking values in G, each of which is defined independently of r. Then the probability that the truth value of Zˆ₁^rZˆ₂ = Yˆ ^s does not agree with the truth value of (g,X₁,X₂,Y,ˆ Zˆ₁,Zˆ₂) being a twin DH tuple is at most 1/p. Moreover, if (g,X₁,X₂,Y,ˆ Zˆ₁,Zˆ₂) is a twin DH tuple, then Zˆ₁^rZˆ₂ = Yˆ ^s certainly holds.

Note that Lemma 1 is a statistical property. Especially, Lemma 1 holds without any number theoretic assumption. To be precise, we consider the following experiment of an algorithm Cheat with unbounded computational power (not limited to PPT), where Cheat, given a triple (g,X₁,X₂), tries to complete a 6-tuple (g,X₁,X₂,Y,ˆ Zˆ₁,Zˆ₂) which passes the “Trapdoor Test” but which is not a twin DH tuple.

ExperimenttwinDH-test_Cheat,G (λ)

(g,X1) ← G2,(r,s) ← Zrgs

G^{3 3} (Y,ˆ Zˆ₁,Zˆ₂) ^← Cheat(g,X₁,X₂)

If Zˆ₁^rZˆ₂ = Yˆ ^s ∧ (g,X₁,X₂,Y,ˆ Zˆ₁,Zˆ₂) is NOT a twin DH tuple,

then return ^Win else return ^Lose

Let us define the advantage of Cheat over G as follows.

AdvtwinDH-test_Cheat,G (λ)

def= Pr[ExperimenttwinDH-test_Cheat,G (λ) returns Win].

Now we are ready to complement Lemma 1.

Lemma 2 (Complement for “Trapdoor Test” [12]) For any algorithm Cheat with unbounded computational power, AdvtwinDH-testCheat,G (λ) is at most 1/p.

For a proof of Lemma 2, see Appendix A.

4 Securing the Waters CP-ABKEM against Chosen-Ciphertext Attacks

In this section, we describe our direct chosenciphertext security technique by applying it to the Waters CP-ABE [4].

Overview of Our Modification The Waters CP-ABE is proved to be secure in the IND-sel-CPA game [4]. We convert it into a scheme that is secure in the INDsel-CCA game by employing the Twin Diffie-Hellman technique of Cash, Kiltz and Shoup [12] and the algebraic trick of Boneh and Boyen [13] and Kiltz [14].

In encryption, a ciphertext becomes to contain additional two elements (d₁,d₂), which function in decryption as a “check sum” to verify that a tuple is certainly a twin DH tuple.

In security proof, the Twin Diffie-Hellman Trapdoor Test does the function instead. It is noteworthy that we are unable to use the bilinear map instead because the tuple to be verified is in the target group. In addition, the algebraic trick enables to answer for adversary’s decryption queries. Note also that the both technique become compatible by introducing random variables.

Key Encapsulation and Encryption. The Waters CP-ABE can be captured as a CP-ABKEM: the blinding factor of the form e(g,g)^αs in the Waters CP-ABE can be considered as a random one-time key. So we call it the Waters CP-ABKEM hereafter and denote it as CP-ABKEM_cpa. Likewise, we distinguish parameters and algorithms of CP-ABKEMcpa by the index _cpa. For theoretical simplicity, we first develop a KEM CP-ABKEM.

4.1      Our Construction

Our CP-ABKEM consists of the following four PPT algorithms (Setup, Encap, KeyGen, Decap). Roughly speaking, the Waters original scheme CP-ABKEM_cpa (the first scheme in [4]) corresponds to the case k = 1 below excluding the “check sum” (d₁,d₂).

Setup(λ,U). Setup takes as input the security parameter λ and the attribute universe U = {1,…,u}. It runs Grp(λ) to get (p,G,GT ,g,e), where G and GT are cyclic groups of order p, e : G × _G → _GT is a bilinear map and g is a generator of G. These become public parameters. Then Setup chooses u random group elements h₁,…,h_u ∈ _G that are associated with the u attributes. In addition, it chooses random exponents α_k ∈ _Zp,k = 1,…,4,a ∈ _Zp and a hash key η ∈ HKey(λ). The public key is published as PK = (g,g^a,h₁,…,h_u,e(g,g)^α1,…,e(g,g)^α4,η). The authority sets MSK = (g^α1,…,g^α4) as the master secret key.

Encap(PK,A). The encapsulation algorithm Encap takes as input the public key PK and an LSSS access structure A = (M,ρ), where M is an l × n matrix and ρ is the function which maps each row index i of M to an attribute in U = {1,…,u}. Encap first chooses a random value s ∈ _Zp that is the encryption randomness, and chooses random values y₂,…,y_n ∈ _Zp. Then Encap forms a vector v~ = (s,y₂,…,y_n). For i = 1 to l, it calculates λ_i = v~ · M_i, where M_i denotes the i-th row vector of M. In addition, Encap chooses random values r₁,…,r_l ∈ _Zp. Then, a pair of a random onetime key and its encapsulation (κ,ψ) is computed as follows.

Put C0 = gs;For i = 1 to l : Ci = gaλi hρ−(rii),Di = gri ; ψ_cpa = (A,C⁰,((C_i,D_i);i = 1,…,l)),τ ^← H_η(ψ_cpa); For k = 1 to 4 : κ_k = e(g,g)^αks;d₁ = κ₁^τκ₃,d₂ = κ₂^τκ₄; (κ,ψ) = (κ₁,(ψ_cpa,d₁,d₂)).

KeyGen(MSK,PK,S). The key generation algorithm KeyGen takes as input the master secret key MSK, the public key PK and a set S of attributes. KeyGen first chooses a random t_k ∈ _Zp,k = 1,…,4. It generates the secret key SK_S as follows.

For k = 1 to 4 : K_k = g^αk g^atk ,L_k = g^tk

For x ∈ S : Kk,x = htxk ;

SK_S = ((K_k,L_k,(K_k,x;x ∈ S));k = 1,…,4).

Decap(PK,ψ,SK_S). The decapsulation algorithm Decap takes as input the public key PK, an encapsulation ψ for an access structure A = (M,ρ) and a private key SK_S for an attribute set S. It first checks whether S ∈ _A. If the result is False, put κˆ =⊥. Otherwise, let I_S = ρ⁻¹(S) ⊂ {1,…,l} and let {ω_i ∈ _Zp;i ∈ I_S} be a set of linear reconstruction constants. Then, the decapsulation κˆ is computed as follows.

Parse ψ into (ψ_cpa = (A,C⁰,((C_i,D_i);i = 1,…,l)),d₁,d₂); τ ← Hη(ψcpa);

For k = 1 to 4 : κˆ_k = e(C0,K_k)/ Y(e(L_k,C_i)e(D_i ωi = e(g,g)αks,Kk,ρ(i)))

i∈IS

If κˆ₁^τκˆ₃ , d₁ ∨ κˆ₂^τκˆ₄ , d₂, then put κˆ =⊥,else put κˆ = κˆ₁.

4.2      Security and Proof

Theorem 1 If the Waters CP-ABKEMcpa [4] is selectively secure against chosen-plaintext attacks and an employed hash function family Hfam has target collision resistance, then our CP-ABKEM is selectively secure against chosenciphertext attacks. More precisely, for any given PPT adversary A that attacks CP-ABKEM in the IND-sel-CCA game where decapsulation queries are at most q_d times, and for any small attribute universe U, there exist a PPT adversary B that attacks CP-ABKEMcpa in the IND-selCPA game and a PPT target collision finder CF on Hfam that satisfy the following tight reduction.

Advind-sel-ccaA_,CP-ABKEM(λ,U)

                    ind-sel-cpa                                     tcr              (λ)+ qd .

             ≤AdvB,CP-ABKEMcpa(λ,U)+AdvCF ,Hfam                     p

Proof. Given any adversary A that attacks our scheme CP-ABKEM in the IND-sel-CCA game, we construct an adversary B that attacks the Waters scheme

CP-ABKEM_cpa in the IND-sel-CPA game as follows. Commit to a Target Access Structure. B is given (λ,U) as inputs, where λ is the security parameter and U = {1,…,u} is the attribute universe. B invokes A on input (λ,U) and gets a target access structure

A = (M ,ρ ) from A, where M is of size l × n . B uses A^∗ as the target access structure of itself and outputs A^∗.

Setup. In return to outputting A^∗, B receives the public key PK_cpa for CP-ABKEMcpa, which consists of the following components.

PK_cpa = (g,g^a,h₁,…,h_u,e(g,g)^α).

To set up a public key PK for CP-ABKEM, B herein needs a challenge instance: B queries its challenger and gets a challenge instance (κ,ψ˜ ). It consists of the following components.

κ˜ = e(g,g)^αs∗ OR a random one-time key κ ∈ KeySp(λ),

 g^s∗,((C_i^∗,D_i^∗);i = 1,…,l^∗)).

Then B makes the rest of parameters of PK as follows.

Choose η ← HKey(λ) and take τ^∗ ← H);

Put e(g,g)^α1 = e(g,g)^α;

Choose γ₁,γ₂ ← _Zp, put e(g,g)^α2 = e(g,g)^γ2/e(g,g)^α1γ1;

Choose µ₁,µ₂ ^← _Zp, put e(g,g)^α3 = e(g,g)^µ1/e(g,g)^α1τ∗,

e(g,g)^α4 = e(g,g)^µ2/e(g,g)^α2τ∗.

Note we have implicitly set relations in the exponent domain:

α2 = γ2 − α1γ1, α3 = µ1 − α1τ∗, α4 = µ2 − α2τ∗ = µ2 − (γ2 − α1γ1)τ∗. (1) A public key PK for CP-ABKEM become:

PK = (PK_cpa,e(g,g)^α2,e(g,g)^α3,e(g,g)^α4,η).

Then B inputs PK into A. Note that PK determines the corresponding MSK uniquely.

Phase 1. B answers for two types of A’s queries as follows.

(1) Key-Extraction Queries. In the case that A issues a key-extraction query for an attribute set S ⊂ U, B has to simulate A’s challenger. To do so, B issues keyextraction queries to B’s challenger for S repeatedly up to four times. As replies, B gets four secret keys of the Waters CP-ABKEM_cpa for a single attribute set S:

SK_cpa,S,k = (K_cpa,k,L_cpa,k,(K_cpa,k,x;x ^{∈ S})),k = 1,…,4.

We remark that, according to the randomness in the key-generation algorithm of the Waters CP-ABKEM_cpa, all four secret keys SK_cpa,S,1,…,SK_cpa,S,4 are random and mutually independent. To reply a secret key SK_S of our CP-ABKEM to A, B converts the four secret keys as follows.

K1 = Kcpa,1, L1 = Lcpa,1, K1,x = Kcpa,1,x,x ^∈ S; K₂ = gγ2Kcpa−γ1,2, L Kcpa−γ,x, x ∈ S;

K,               L Kcpaτ∗ ,3,x, x ∈ S;

K Kcpaγ₁τ,^∗4,x, x ∈ S.

Then B replies SK_S = ((K_k,L_k,(K_k,x;x ∈ S));k = 1,…,4) to A.

(2) Decapsulation Queries. In the case that A issues a decapsulation query for (S,ψ), where S ⊂ U is an attribute set and ψ = (ψ_cpa,d₁,d₂) is an encapsulation concerning A, B has to simulate A’s challenger. To do so, B computes the decapsulation result κˆ as follows.

If S <A then put κˆ =⊥,

else

τ ← Hη(ψcpa);

Yˆ = e(C⁰,g)^τ−τ∗,Zˆ₁ = d₁/e(C⁰,g)^µ1,Zˆ₂ = d₂/e(C⁰,g)^µ2;

If Zˆ1γ1Zˆ2 , Yˆ γ2 (: call this checking TwinDH-Test) then put κˆ = κˆ₁ =⊥

else

If τ = τ^∗ then abort (: call this case Abort) else κˆ = κˆ1 = Zˆ11/(τ−τ∗).

Challenge. In the case that A queries its challenger for a challenge instance, B makes a challenge instance as follows.

Put d;

                   Put ψ ψ ,d            .

Then B feeds (κ,ψ˜    ^∗) to A as a challenge instance.

Phase 2. The same as in Phase 1.

Guess. In the case that A returns A’s guess b^˜, B returns b^˜ itself as B’s guess.

In the above construction of B, B can perfectly simulate the real view of A until the case Abort happens, except for a negligible case, and hence the algorithm A works as designed. To see the perfect simulation with a negligible exceptional case, we are enough to prove the following seven claims.

Claim 1 The reply SK_S = ((K_k,L_k,(K_k,x;x ∈ S));k = 1,…,4) for a key-extraction query of A is a perfect simulation.

Proof. We must consider the implicit relations (1). For the index 2, we have implicitly set the randomness t₂ = t_cpa,2(−γ₁) and we get:

K₂ = gγ2Kgatcpa,2)⁻γ1

= gγ2(gα1gat2/(−γ1))−γ1 = gγ2−α1γ1gat2 = gα2gat2,

Lgtcpa,2)⁻γ1 = gt2,

                       ⁻γ₁                           tcpa,2

          K2,x = ^K_cpa,2_,x = (hx                            )S.

For the index 3 and 4, see Appendix B.

Claim 2 (e(g,g), e(g,g)^α1, e(g,g)^α2, Y,ˆ Zˆ₁, Zˆ₂) is a twin Diffie-Hellman tuple if and only if (e(g,g), e(g,g)^α1τe(g,g)^α3, e(g,g)^α2τe(g,g)^α4, e(C⁰,g), d₁, d₂) is a twin Diffie-Hellman tuple.

Proof. This claim can be proved by a short calculation.

See Appendix C.

Claim 3 If (e(g,g),e(g,g)^α1,e(g,g)^α2,Y,ˆ Zˆ₁,Zˆ₂) is a twin

Diffie-Hellman tuple, then (Y,ˆ Zˆ₁,Zˆ₂) certainly passes the TwinDH-Test: Z^ˆ₁^γ1Z^ˆ₂ = Yˆ γ².

Proof. This claim is a direct consequence of Lemma 1.

Claim 4 Consider the following event which we name as Overlooki:

In the i-th ^TwinDH-Test, the following condition holds:

          

Zˆ1γ1Zˆ2 = Yˆ γ2 holds and (e(g,g),e(g,g)α1,e(g,g)α2,Y,ˆ Zˆ1,Zˆ2) is NOT a twin DH tuple.

Then, for at most q_d times decapsulation queries of A, the probability that at least one ^Overlooki occurs is negligible in λ. More precisely, the following inequality holds:

qd

_

Pr[ Overlook_i] ≤ q_d/p.             (2) i=1

Proof. To apply Lemma 2, we construct an algorithm Cheat_λ,U with unbounded computational power, which takes as input (e(g,g),e(g,g)^α1,e(g,g)^α2) and returns (Y,ˆ Zˆ₁,Zˆ₂) employing the adversary A as a subroutine. Fig. 1 shows the construction.

First, note that the view of A in Cheat_λ,U is the same as the real view of A and hence the algorithm A works as designed.

Second, note that the return (Y,ˆ Zˆ₁,Zˆ₂) of Cheat_λ,U is randomized in TABLE. Hence:

qd   qd X 1      1 X

 Pr[Overlook_i] =                      Pr[Overlook_i] i=1 qd                 qd i=1

  =AdvtwinDH-test_Cheatλ,U _,G (λ).                                                (3)

Third, applying Lemma 2 to Cheat_λ,U , we get:

                        AdvtwinDH-test_Cheatλ,U _,G (λ) ≤ 1/p.                  (4)

Combining (3) and (4), we have:

                      qd                                                           qd

                       _                              X

Pr[ Overlooki] ≤   Pr[Overlooki] i=1   i=1

≤q_dAdvtwinDH-test_Cheatλ,U _,G (λ) ≤ ^qpd .

Claim 5 The probability that ^Overlooki never occurs in TwinDH-Test for every i and Abort occurs is negligible in λ. More precisely, the following inequality holds:

qd

Pr[^¬Overlook_i ∧ Abort] ≤ Advtcr_{CF ,Hfam}(λ). (5) i=1

Proof. This claim is proved by constructing a collision finder CF on Hfam. See Appendix D.

Claim 6 The reply κˆ to A as an answer for a decapsulation query is correct.

Claim 7 The challenge instance  is correctly distributed.

Proof. These two claims are proved by a direct calculation. See Appendices E and F, respectively.

Evaluation of the Advantage of B. Now we are ready to evaluate the advantage of B in the IND-sel-CPA game. That A wins in the IND-sel-CCA game means that (κ,ψ˜ ^∗ )) is correctly guessed. This is equivalent to that (κ,ψ^˜ _cpa^∗ ) is correctly guessed because  determines the consistent blinding factor κ^∗ = e(g,g)^αs∗ uniquely. This means that B wins in the IND-sel-CPA game.

Figure 1: An Algorithm Cheat_λ,U with Unbounded Computational Power for a Proof of Claim 4.

Therefore, the probability that B wins is equal to the probability that A wins, Overlooki never holds in TwinDH-Testfor each i and Abort never occurs. So we have:

This is what we should prove in Theorem 1.

4.3 Encryption Scheme from KEM

It is straightforward to construct our encryption scheme CP-ABE from CP-ABKEM. The IND-sel-CCA security of CP-ABE is proved based on IND-sel-CPA security of the Waters KEM CP-ABKEMcpa. Setup(λ,U). The same as Setup of CP-ABKEM.

Encrypt(PK,A,m). The same as Encap of CP-ABKEM except that Encrypt multiplies m by the blinding factor κ in the group G_T . Encrypt returns CT = (C = mκ,ψ = (ψ_cpa,d₁,d₂)).

KeyGen(MSK,PK,S).               The    same    as    KeyGen    of

CP-ABKEM.

Decrypt(PK,CT,SK_S). The same as Decap of CP-ABKEM except that Decrypt divides out C by the decapsulated blinding factor κˆ. Decrypt returns the result mˆ.

4.4      Security and Proof

Theorem 2 If the Waters CP-ABKEMcpa [4] is selectively secure against chosen-plaintext attacks and an employed hash function family Hfam has target collision resistance, then our CP-ABE is selectively secure against chosenciphertext attacks. More precisely, for any given PPT adversary A that attacks CP-ABE in the IND-sel-CCA game where decryption queries are at most q_d times, and for any small attribute universe U, there exist a PPT adversary B that attacks CP-ABKEM_cpa in the IND-sel-CPA game and a PPT target collision finder CF on Hfam that satisfy the following inequality.

Advind-sel-cca_A,CP-ABE (λ,U)

≤2AdvBind-sel-cpa,CP-ABKEMcpa(λ,U)+AdvtcrCF ,Hfam(λ)+ qpd .

Proof. Given any adversary A that attacks our scheme CP-ABE in the IND-sel-CCA game, we construct an adversary B that attacks the Waters KEM CP-ABKEM_cpa in the IND-sel-CPA game as follows. Commit to a Target Access Structure. The same as that of CP-ABKEM.

Setup. In return to outputting A^∗, B receives the public key PK_cpa for CP-ABKEMcpa. To set up a public key PK for CP-ABE, B herein needs a challenge instance:

B queries its challenger and gets a challenge instance

). The rest of procedure is the same as that of

CP-ABKEM, and B inputs PK into A. Phase 1. The same as that of CP-ABKEM except that B replies a decrypted message mˆ to A for a decryption query.

Challenge. In the case that A submits two plaintexts

) of equal length, B makes a challenge ciphertext CT as follows and feeds CT^∗ to A.

Choose b⁰ ← {0,1}, put C˜^∗ = m^∗_b0 κ˜;

Put d(C0∗,g)µ1,d2∗ = e(C0∗,g)µ2;

Put CT.

Phase 2. The same as in Phase 1.

Guess. In the case that A returns A’s guess b^˜, B returns b^˜ as B’s guess.

Evaluation of the Advantage of B. A standard argument deduces a loss of tightness by a factor of 1/2. That is;

ind-sel-cpa

Adv_B,CP-ABKEM_cpa(λ,U)

≥12Advind-sel-ccaA_,CP-ABE (λ,U) − ^qpd − AdvtcrCF _,Hfam(λ).

5 Securing the Ostrovsky-SahaiWaters KP-ABKEM against Chosen-Ciphertext Attacks

In this section, we describe our direct chosenciphertext security modification by applying it to the Ostrovsky-Sahai-Waters KP-ABE [11]. Overview of Our Modification The Ostrovsky-Sahai-Waters KP-ABE is proved to be secure in the IND-selCPA game [11]. We convert it into a scheme that is secure in the IND-sel-CCA game by employing the Twin Diffie-Hellman technique of Cash, Kiltz and Shoup [12] and the algebraic trick of Boneh and Boyen [13] and Kiltz [14].

In encryption, a ciphertext becomes to contain additional two elements (d₁,d₂), which function in decryption as a “check sum” to verify that a tuple is certainly a twin DH tuple.

In security proof, the Twin Diffie-Hellman Trapdoor Test does the function instead. It is noteworthy that we are unable to use the bilinear map instead because the tuple to be verified is in the target group. In addition, the algebraic trick enables to answer for adversary’s decryption queries. Note also that the both technique become compatible by introducing random variables.

Key Encapsulation and Encryption. The Ostrovsky-Sahai-Waters KP-ABE can be captured as a KP-ABKEM: the blinding factor of the form e(g,g)^aαs in the Ostrovsky-Sahai-Waters KP-ABE can be considered as a random one-time key. So we call it the Ostrovsky-Sahai-Waters KP-ABKEM hereafter and denote it as KP-ABKEM_cpa. Likewise, we distinguish parameters and algorithms of KP-ABKEM_cpa by the index _cpa. For theoretical simplicity, we first develop a KEM KP-ABKEM.

5.1       Our Construction

Our KP-ABKEM consists of the following four PPT algorithms (Setup, Encap, KeyGen, Decap). Roughly speaking, the Ostrovsky-Sahai-Waters original scheme KP-ABKEM_cpa (the first scheme in [11]) corresponds to the case k = 1 below excluding the “check sum” (d₁,d₂).

Setup(λ,U). Setup takes as input the security parameter λ and the attribute universe U = {1,…,u}. It runs Grp(λ) to get (p,G,GT ,g,e), where G and GT are cyclic groups of order p, e : G → _GT is a bilinear map and g is a generator of G. These become public parameters. Then Setup chooses u random group elements h₁,…,h_u ∈ _G that are associated with the u attributes. In addition, it chooses random exponents α_k ∈ _Zp,k = 1,…,4,a ∈ _Zp and a hash key η ∈ HKey(λ). The public key is published as PK = (g,g^a,h₁,…,h_u,e(g,g)^aα1,…,e(g,g)^aα4,η). The authority sets MSK = (α₁,…,α₄) as the master secret key. Encap(PK,S). The encapsulation algorithm Encap takes as input the public key PK and a set S of attributes. Encap first chooses a random value s ∈ _Zp that is the encryption randomness. Then, a pair of a random one-time key and its encapsulation (κ,ψ) is computed as follows.

Put C⁰ = g^s;For x ∈ S : C_x = h^s_x ψcpa = (S,C0,(Cx;x ∈ S)),τ ← Hη(ψcpa); For k = 1 to 4 : κ_k = e(g,g)^aαks;d₁ = κ₁^τκ₃,d₂ = κ₂^τκ₄; (κ,ψ) = (κ₁,(ψ_cpa,d₁,d₂)).

KeyGen(MSK,PK,A). The key generation algorithm KeyGen takes as input the master secret key MSK, the public key PK and an LSSS access structure A = (M,ρ), where M is an l ×n matrix and ρ is the function which maps each row index i of M to an attribute in U = {1,…,u}. For k = 1 to 4, KeyGen first chooses random values y_k,2,…,y_k,n ∈ Z_p and forms a vector v~_k = (α_k,y_k,2,…,y_k,n). Then, for i = 1 to l, it calculates λ_k,i = v~_k · M_i, where M_i denotes the i-th row vector of M, and it chooses random values r_k,i ∈ _Zp. KeyGen generates the secret key SK_A as follows.

For k = 1 to 4 : For l = 1 to l :

Kk,i = gaλk,i hrρk,i(i),Lk,i = grk,i

SK_A = (((K_k,i,L_k,i);i = 1,…,l)k = 1,…,4).

Decap(PK,ψ,SK_A). The decapsulation algorithm Decap takes as input the public key PK, an encapsulation ψ for an attribute set S and a private key SK_A for an access structure A = (M,ρ). It first checks whether S ∈ _A. If the result is False, put κˆ =⊥. Otherwise, let I_S = ρ⁻¹(S) ⊂ {1,…,l} and let {ω_i ∈ _Zp;i ∈ I_S} be a set of linear reconstruction constants. Then, the decapsulation κˆ is computed as follows.

Parse ψ into (ψ_cpa = (S,C⁰,(C_x;x ∈ S)),d₁,d₂); τ ← Hη(ψcpa);

For k = 1 to 4 :

                     ^Y          0                                            ωⁱ

          κˆk =           (e(C ,K_k,i)/e(L_k,i,Cρ(i₎))         = e(g,g)aα^ks

i∈IS

If κˆ₁^τκˆ₃ , d₁ ∨ κˆ₂^τκˆ₄ , d₂, then put κˆ =⊥,else put κˆ = κˆ₁.

5.2       Security and Proof

Theorem 3 If the Ostrovsky-Sahai-Waters KP-ABKEM_cpa [11] is selectively secure against chosen-plaintext attacks and an employed hash function family Hfam has target collision resistance, then our KP-ABKEM is selectively secure against chosen-ciphertext attacks. More precisely, for any given PPT adversary A that attacks KP-ABKEM in the IND-sel-CCA game where decapsulation queries are at most q_d times, and for any small attribute universe U, there exist a PPT adversary B that attacks KP-ABKEM_cpa in the IND-sel-CPA game and a PPT target collision finder CF on Hfam that satisfy the following tight reduction.

Advind-sel-ccaA_,KP-ABKEM(λ,U)

≤AdvBind-sel-cpa,KP-ABKEMcpa(λ,U)+AdvtcrCF ,Hfam(λ)+ qpd .

Proof. We will omit the description of the proof because the proof goes analogously to the case of CP-

ABKEM in Section 4.2.

5.3        Encryption Scheme from KEM

It is straightforward to construct our encryption scheme KP-ABE from KP-ABKEM. The IND-sel-CCA security of KP-ABE is proved based on IND-sel-CPA security of the Waters KEM KP-ABKEMcpa. Setup(λ,U). The same as Setup of KP-ABKEM. Encrypt(PK,A,m). The same as Encap of KP-ABKEM except that Encrypt multiplies m by the blinding factor κ in the group G_T . Encrypt returns CT = (C = mκ,ψ = (ψ_cpa,d₁,d₂)).

KeyGen(MSK,PK,S).                           The same as KeyGen of

KP-ABKEM.

Decrypt(PK,CT,SK_S). The same as Decap of KP-ABKEM except that Decrypt divides out C by the decapsulated blinding factor κˆ. Decrypt returns the result mˆ.

5.4      Security and Proof

Theorem 4 If the Ostrovsky-Sahai-Waters KP-ABKEM_cpa [11] is selectively secure against chosen-plaintext attacks and an employed hash function family Hfam has target collision resistance, then our KP-ABE is selectively secure against chosen-ciphertext attacks. More precisely, for any given PPT adversary A that attacks KP-ABE in the INDsel-CCA game where decryption queries are at most q_d times, and for any small attribute universe U, there exist a PPT adversary B that attacks KP-ABKEMcpa in the IND-sel-CPA game and a PPT target collision finder CF on Hfam that satisfy the following inequality.

Advind-sel-cca_A,KP-ABE (λ,U)

≤2AdvBind-sel-cpa,KP-ABKEMcpa(λ,U)+AdvtcrCF ,Hfam(λ)+ qpd .

Proof. We will omit the description of the proof because the proof goes in the same way as the case of

CP-ABE in Section 4.4.

6 Efficiency Discussion

First of all, we remark that our individual modification to attain CCA security is applicable when a DiffieHellman tuple to be verified is in the target group of a bilinear map e : G × _G → _GT . Especially, it is applicable even when an original CPA secure scheme is based on asymmetric pairing [19], e : G₁ × _G2 → _GT . For example, the Type 3 version [19] of the Waters CP-ABE scheme [4] can be found in [20]. Detailed discussions and results on real implementations are found for the case of CPA-secure ABE schemes [21, 20]. We note here that the efficiency comparison below enables to guess the implementation results of CCA-secure ABE schemes via our modification.

We compare the efficiency of our CP-ABE with the original Waters CP-ABEcpa, and our KP-ABE with the original Ostrovsky-Sahai-Waters KP-ABE_cpa. We also compare the efficiency of our schemes with the CCAsecure CP-ABE and KP-ABE schemes obtained by the generic transformation in [10]. Here the generic transformation [10] is considered in the case of a small attribute universe, the delegation type [10] and the Lamport one-time signature [22]. Table 1 shows these comparison. Note that a hash function is applied to generate a message digest of bit-length λ before signing by a secret key of the one-time signature. Note also, for simplicity, we evaluate the lengths and the amounts of computation below in the case that an access structure A is “all-AND” and an attribute map ρ is injective (i.e “single-use” that is opposed to “multiuse”).

Table 1: Efficiency comparison of IND-sel-CCA secure ABEs ([10] and ours) with the original IND-sel-CPA secure ABEs [4, 11].

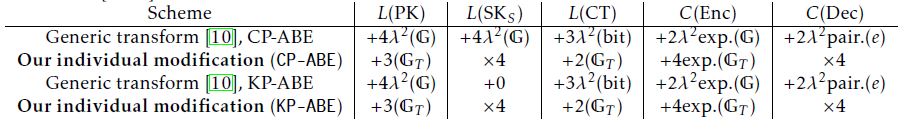
Our individual modification results in expansion of the length of a secret-key and the amount of decryption computation by a factor of four, while the length of a public-key, the length of a ciphertext and the amount of encryption computation are almost the same as those of the original CPA-secure schemes. In the case that the size of an attribute set is up to ( of) the square of the security parameter λ, the amount of decryption computation of our CP-ABE and KP-ABE are smaller than those of the CP-ABE and KP-ABE obtained by the generic transformation [10], respectively.tion by the map e, respectively.

7 Conclusion

We demonstrated direct chosen-ciphertext security modification for ABE in the standard model in the case of the Waters scheme (CP-ABKEM_cpa, CP-ABE_cpa) and the Ostrovsky-Sahai-Waters scheme(KP-ABKEMcpa, KP-ABEcpa). We utilized the Twin DiffieHellman Trapdoor Test of Cash, Kiltz and Shoup and the algebraic trick of Boneh and Boyen [13] and Kiltz [14]. Our modification worked for the setting that the Diffie-Hellman tuple to be verified in decryption was in the target group of the bilinear map. We compared the efficiency of our CCA-secure ABE schemes with the original CPA-secure ABE schemes and with the CCA-secure ABE schemes obtained by the versatile generic transformation.

Acknowledgment

This work was supported by JSPS KAKENHI Grant Number JP15K00029.

Appendix

A Proof of Lemma 2

The only one point to be complemented to the original proof (in [12]) is that even for any algorithm A with unbounded computational power, the statement holds. This is because, conditioning on the input fixed values (g,X1,X2), A only reduces the twodimensional freedom (r,s) ∈_Z²_p into the one-dimensional freedom r ∈_Zp even if A correctly guesses the relation s = rx1 +x2.

B Proof of Claim 1

For the index 3, we have implicitly set t3 = tcpa,3(−τ^∗) and we get:

 

C Proof of Claim 2

Suppose that we are given a twin DH tuple (e(g,g),e(g,g)^α1,e(g,g)^α2, Y,ˆ Zˆ₁,Zˆ₂). Then, di/e(C⁰,g)^µi = (e(g,g)^αi )^{s(τ−τ∗)},i = 1,2. So, using the implicit relations (1), we have:

∗        ∗ di = e(g,g)αis(τ−τ )e(gs,g)µi = (e(g,g)αi(τ−τ )e(g,g)µi )s

=(e(g,g)^αi(τ−τ∗⁾e(g,g)αiτ∗+α(i+2))s = (e(g,g)αiτe(g,g)α(i+2))s,i = 1,2.

This means that (e(g,g), e(g,g)^α1^τe(g,g)^α3, e(g,g)^α2^τe(g,g)^α4, e(C⁰,g), d1, d2) is a twin Diffie-Hellman tuple.

The converse is also verified by the reverse calculation.

D Proof of Claim 5

To reduce to the target collision resistance of an employed hash function family Hfam, we construct a PPT target collision finder CF that attacks Hfam using A as a subroutine. The construction is shown in Fig.2. (Note that the case Collision is defined in Fig.2.)

Note that the view of A in CF is the same as the real view of A until the case Collision occurs and hence the algorithm A works as designed.

To evaluate the probability in Claim 5, we consider the following two cases.

Case 1: the case that Abort (τ = τ^∗) occurs in B in Phase 1. In this case, the target τ^∗ has not been given to A. So A needs to guess τ^∗ to cause a collision τ = τ^∗. Hence:

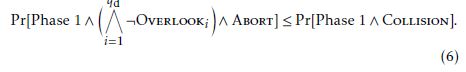Case 2: the case that Abort (τ = τ^∗) occurs in B in Phase 2. In this case, if, in addition to τ = τ^∗, it occurred that  (and hence C⁰ = C^0∗), then it would occur that ψ = ψ^∗. This is because the following two tuples are equal twin DH tuples by the fact that ^Overlooki never occurs:

(e(g,g),e(g,g)^α1τe(g,g)^α3,e(g,g)^α2τe(g,g)^α4,e(C⁰,g),d1,d2),

Hence both S ∈_A and ψ = ψ^∗ would occur. This is ruled out in decapsulation query; a contradiction. So we have ψcpa , ψ_cpa^∗                    ; that is, a collision: ψ_cpa ,.

Therefore, if Overlooki never occurs for each i, then only decapsulation queries for which (e(g,g), e(g,g)^α1, e(g,g)^α2, Y,ˆ Zˆ₁, Zˆ₂) are certainly twin DH tuples have the chance to cause a collision τ = τ^∗, as is the case in CF . Hence we have:

^qd   Pr[Phase 2∧                                ¬Overlook_i ∧Abort] ≤ Pr[Phase 2∧Collision].

i=1 (7)

Figure 2: A PPT Collision Finder CF that attacks Hfam for the proof of Claim 5.

 

1. Amit Sahai and Brent Waters. Fuzzy identity-based encryption. In Advances in Cryptology – EUROCRYPT 2005, 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, May 22-26, 2005, Proceedings, pages 457–473, 2005.
2. Vipul Goyal, Omkant Pandey, Amit Sahai, and Brent Waters. Attribute-based encryption for fine-grained access control of encrypted data. In Proceedings of the 13th ACM Conference on Computer and Communications Security, CCS 2006, Alexandria, VA, USA, Ioctober 30 – November 3, 2006, pages 89–98, 2006.
3. John Bethencourt, Amit Sahai, and Brent Waters. Ciphertextpolicy attribute-based encryption. In 2007 IEEE Symposium on Security and Privacy (S&P 2007), 20-23 May 2007, Oakland, California, USA, pages 321–334, 2007.
4. Brent Waters. Ciphertext-policy attribute-based encryption: An expressive, efficient, and provably secure realization. In Public Key Cryptography – PKC 2011 – 14th International Conference on Practice and Theory in Public Key Cryptography, Taormina, Italy, March 6-9, 2011. Proceedings, pages 53–70, 2011.
5. Allison B. Lewko, Tatsuaki Okamoto, Amit Sahai, Katsuyuki Takashima, and Brent Waters. Fully secure functional encryption: Attribute-based encryption and (hierarchical) inner product encryption. In Advances in Cryptology – EUROCRYPT 2010, 29th Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, May 30 – June 3, 2010. Proceedings, pages 62–91, 2010.
6. Hiroaki Anada and Seiko Arita. Short cca-secure ciphertextpolicy attribute-based encryption. In 2017 IEEE International Conference on Smart Computing, SMARTCOMP 2017, Hong Kong, China, May 29-31, 2017, pages 1–6, 2017.
7. Ran Canetti, Shai Halevi, and Jonathan Katz. Chosenciphertext security from identity-based encryption. In Advances in Cryptology – EUROCRYPT 2004, International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, May 2-6, 2004, Proceedings, pages 207– 222, 2004.
8. Dan Boneh and Xavier Boyen. Efficient selective-id secure identity-based encryption without random oracles. In Advances in Cryptology – EUROCRYPT 2004, International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, May 2-6, 2004, Proceedings, pages 223–238, 2004.
9. Xavier Boyen, Qixiang Mei, and Brent Waters. Direct chosen ciphertext security from identity-based techniques. In Proceedings of the 12th ACM Conference on Computer and Communications Security, CCS 2005, Alexandria, VA, USA, November 7-11, 2005, pages 320–329, 2005.
10. Shota Yamada, Nuttapong Attrapadung, Goichiro Hanaoka, and Noboru Kunihiro. Generic constructions for chosenciphertext secure attribute based encryption. In Public Key Cryptography – PKC 2011 – 14th International Conference on Practice and Theory in Public Key Cryptography, Taormina, Italy, March 6-9, 2011. Proceedings, pages 71–89, 2011.
11. Rafail Ostrovsky, Amit Sahai, and Brent Waters. Attributebased encryption with non-monotonic access structures. In Proceedings of the 2007 ACM Conference on Computer and Communications Security, CCS 2007, Alexandria, Virginia, USA, October 28-31, 2007, pages 195–203, 2007.
12. David Cash, Eike Kiltz, and Victor Shoup. The twin diffiehellman problem and applications. In Advances in Cryptology – EUROCRYPT 2008, 27th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Istanbul, Turkey, April 13-17, 2008. Proceedings, pages 127–145, 2008.
13. Dan Boneh and Xavier Boyen. Efficient selective-id secure identity-based encryption without random oracles. In Advances in Cryptology – EUROCRYPT 2004, International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, May 2-6, 2004, Proceedings, pages 223–238, 2004.
14. Eike Kiltz. Chosen-ciphertext security from tag-based encryption. In Theory of Cryptography, Third Theory of Cryptography Conference, TCC 2006, New York, NY, USA, March 4-7, 2006, Proceedings, pages 581–600, 2006.
15. Choudary Gorantla, Colin Boyd, and Juan Manuel Gonz´alez Nieto. Attribute-based authenticated key exchange. In Information Security and Privacy – 15^th Australasian Conference, ACISP 2010, Sydney, Australia, July 5-7, 2010. Proceedings, pages 300–317, 2010.
16. Nuttapong Attrapadung, Benoˆit Libert, and Elie de Panafieu. Expressive key-policy attribute-based encryption with constant-size ciphertexts. In Public Key Cryptography – PKC 2011 – 14th International Conference on Practice and Theory in Public Key Cryptography, Taormina, Italy, March 6-9, 2011. Proceedings, pages 90–108, 2011.
17. Nuttapong Attrapadung. Dual system encryption via doubly selective security: Framework, fully secure functional encryption for regular languages, and more. In Advances in Cryptology – EUROCRYPT 2014 – 33rd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Copenhagen, Denmark, May 11-15, 2014. Proceedings, pages 557–577, 2014.
18. Moni Naor and Moti Yung. Universal one-way hash functions and their cryptographic applications. In Proceedings of the 21^st Annual ACM Symposium on Theory of Computing, May 14-17, 1989, Seattle, Washigton, USA, pages 33–43, 1989.
19. Steven D. Galbraith, Kenneth G. Paterson, and Nigel P. Smart. Pairings for cryptographers. Discrete Applied Mathematics, 156(16):3113–3121, 2008.
20. Eric Zavattoni, Luis J. Dominguez Perez, Shigeo Mitsunari, Ana H. S´anchez-Ram´irez, Tadanori Teruya, and Francisco Rodr´iguez-Henr´iquez. Software implementation of an attribute-based encryption scheme. IEEE Trans. Computers, 64(5):1429–1441, 2015.
21. Ana Helena S´anchez and Francisco Rodr´iguez-Henr´iquez. NEON implementation of an attribute-based encryption scheme. In Applied Cryptography and Network Security – 11^th International Conference, ACNS 2013, Banff, AB, Canada, June 25-28, 2013. Proceedings, pages 322–338, 2013.
22. Lamport. Constructing digital signatures from a one-way function. Technical report, October 1979.

(Click to view)

(Click to view)