1. Introduction

This article is an extension of a paper previously presented in the international conference of ubiquitous and future networks 2018 (ICUFN 2018) [1]. The great works of Watts and Strogatz [2] which focused on investigation of complex networks have witnessed a tremendous attention from many scientific communities because of the theoretical importance and practical implementation of such outcome in areas such as computer networks, social networks, biological networks, communication networks, electric power grid, food webs and transportation networks [3, 4, 5, 6, 7, 8]. Complex dynamical networks (CDNs) are large number of interconnected nodes with each node having some defined contents. Majority of these networks display some level of complexities in their overall topology as well as dynamical properties [9]. Amongst the important collective behaviors of CDNs is synchronization problem. This behavior has been investigated by many profound researchers [10, 11]. Synchronization of a network is related to subsystems been represented as nodes in coupled systems in which the various nodes with different initial conditions converge to a common behavioral trajectory. Many control methodologies have been proposed to ensure the solution to synchronization problems, amongst such control methods are pinning control [12], sampled data control [13], sliding mode control [14], impulsive control [15] and so on. The tendencies of sudden changes in network coupling which can emanate from internal and external environmental factors such as unexpected change of working environment, random link failures and repairs on network connectivity result in stochastic behavior in the network coupling. Additionally, the practical implementation of control design might not be precise because of limited information speed, round-off error of numerical computations, aging of system components, analogy to digital conversions (ADC) and Digital to analogy conversion (DAC) [13]. Controller fragility refers to the variation effects on the control parameters as cited in [16]. This problem is addressed in the design of a nonfragile control scheme which is presented to address controller gain fluctuation based on the aforementioned shortfalls as presented in [17, 18].

Time delays which are ubiquitous in nature and present in CDNs, possess the ability to destroy synchronization performance which can lead to oscillation and instability of the network, hence the need to consider it when addressing synchronization issues of CDNs. It is very important to also note that, there exit time delays in the exchange of information resulting from finite transmission speed in the network, memory effect, limited bandwidth and so on [19]. From the aforementioned discussions, we are motivated in this paper to seek solutions to CDNs synchronization with nonfragile control design scheme, taking into consideration the stochastic coupling nature of the network. The important contributions of this paper are summarized as follows:

1. The problem of CDNs robust synchronization with stochastic coupling and time-varying delays is studied permitting some level of control gain uncertainties.
2. Control scheme with non-fragile characteristics is designed and presented which guarantee the system error synchronization.
3. A suitable Lyapunov Krasovskii functional (LKF) is chosen which applied the extended Jensen’s integral inequality.
4. Given are two numerical examples which indicate the usefulness of our proposed control approach.

2. Model description and Preliminaries

In this paper, standard notations are used. Rⁿ shows the Euclidean n- dimensional space, R^m×n denotes the set of all m×n real matrices. I and 0 represent identity and zero matrices with appropriate dimensions, respectively. P > 0 is a real positive symmetric definite matrix. The superscript “T” indicates transposition. Also, an asterisk(∗) is used to show the symmetric terms and diag{….} represent a diagonal block matrix. All other matrices without given dimensions are considered to be of compatible dimensions. In this paper, the robust synchronization of CDNs which entail the stochastic coupling of N identical nodes with time varying delays is described as follows:

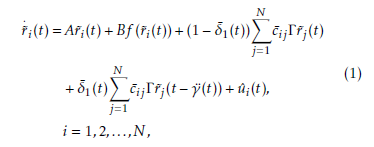Where, r˜_i(t) = (r˜_i1(t),r˜_i2(t),…,r˜_in(t))^T ∈ _Rⁿ denotes the state vector of the i^th node, uˆ_i(t) ∈ _Rⁿ. A,B are known real constant matrices and they are assumed to be stabilizable, f : Rⁿ → _Rⁿ indicate a smooth nonlinear function, Γ ∈ _R^n×n is the inner coupling matrix of the nodes and C¯ = (c¯_ij)_N×_N represent the outer coupling configuration of the network. If there is a connection from node i to node j (i , j), then the coupling matrix c¯_ij , 0; otherwise c¯_ij = 0. Furthermore, the diagonal

N

elements are defined as c¯_ii = − ^P c¯_ij. γ¨(t) represent j=1,j,i

time-varying delay which is considered to be a differentiable function that satisfies the following conditions:

δ¯₁(t) ∈ _R denotes a stochastic variable, which is in the form of a Bernoulli distribution sequence defined by

δ¯₁(t) =

Below indicates the stochastic probability variable δ¯₁(t):

P r{δ^¯₁(t) = 1} = δ^¯₁,

P r{δ¯₁(t) = 0} = 1 − δ¯₁,

where δ¯₁ ∈ [0,1] is a known constant. Then, the supposed initial condition for (1) is given by r˜_i(t) = ψ¯_i(t), t ∈ [−γ¨₂,0] and i = 1,…,N.

Assumption 2.1 [20] The continuous vector valued function f (•) : Rⁿ → _Rⁿ is considered which satisfies f (0) = 0, hence this sector-bounded condition stands:

[f (x)−f (y)−Z₁(x−y)]^T [f (x)−f (y)−Z₂(x−y)] ≤ 0, (3)

given that Z₁ and Z₂ are constant matrices of appropriate size. From (1) and using kronecker properties, we have

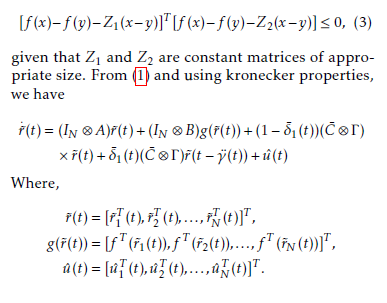Lemma 2.1 ([21] Jensen inequality) Given a matrix H = H^T > 0, of an appropriate dimension and a vector function α¯(·) : [0 γ¯] → _Rⁿ for a scalar γ >¯ 0, the integration is defined as follows:

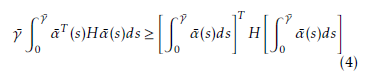Lemma 2.2 [22] For constant matrices L =  L11 L12!, L ∈ R2n×2n, U˜ = U˜ T > 0, U˜ ∈ Rn×n, a con-

L21            L22

tinuous function satisfying d₁ ≤ d(t) ≤ d₂, and a continuously differentiable function x : [−d₂,0] → _Rⁿ such that the integration is properly defined, hence the following inequality holds: Rtt₋−_dd21 T

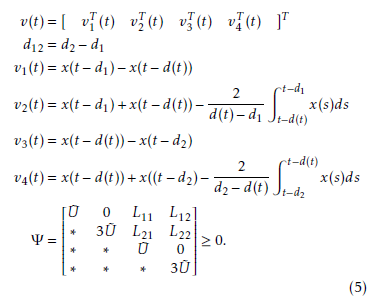Remark 1. The Lemma (2.2) is derived from the reciprocal convex combination techniques with Jensen inequality resulting in the less conservativeness of our results. The detailed proof is omitted but can be referred from [22].

Lemma 2.3 (Schur Complement [23]): For a given matrix any of the inequalities below is equivalent to Λ :

1. Λ11 < 0, Λ22 − ΛT12Λ−111Λ12 < 0
2. Λ22 < 0, Λ11 − Λ12Λ−221ΛT12 < 0

Lemma 2.4 [6], Suppose Q = Q^T , R and T been real appropriate dimension matrices and the function F(t) which satisfies the condition F^T (t)F(t) < I. Accordingly, Q + RF(t)T + T ^T F^T (t)R^T < 0 when a given scalar  > 0 exist. Then,

Definition 1 The CDNs (1) is synchronized when the condition below holds:

Consider the dynamics of an isolated unforced node s(t) to be s˙(t) = As(t) + Bf (s((t))). s(t) can be taken as an equilibrium point, periodic orbit, or even a chaotic attractor.

Let the i^th node error system be given as e_i(t) = r˜_i(t) − s(t). Consequently, error dynamics of CDNs (1) is given by:

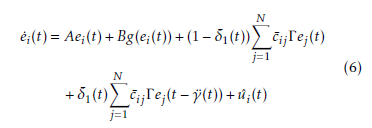The designed control scheme to guarantee synchronization of the CDNs is:

uˆ_i(t) = (k_i +σ(t)4k_i(t))e(t)+k_τe(t−γ¨(t)), i = 1,2,…,N. (7) Consider k_i,k_τ ∈ _R^n×n as the feedback controller gain matrices which are yet to be estimated. Also, 4k_i represent the gain fluctuation, where 4k_i(t) is known as follows:

4ki(t) ≡ HiΥi(t)Wi

where Υ_i(t) ∈ _R^k×l, is an unknown time-varying matrix which satisfies the condition: Υ_i(t)^T Υ_i(t) ≤ I, H_i and W_i are matrices of known parameters. The probability variable σ(t) shows controller gains fluctuations. The random occurring fluctuations of the gain obeys the

Bernoulli distribution with the following definition and the probability of stochastic parameter σ(t) is given as:

P r{σ(t) = 1} = σ

                        P r{σ(t) = 0} = 1 − σ;        σ ∈ [0,1]

Closed loop of the error dynamics (6) of the CDNs yields:

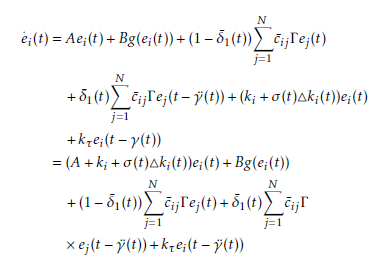
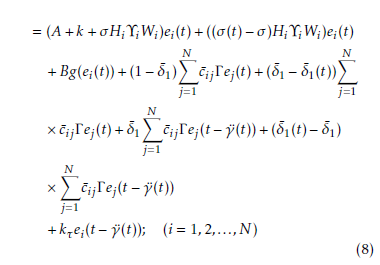
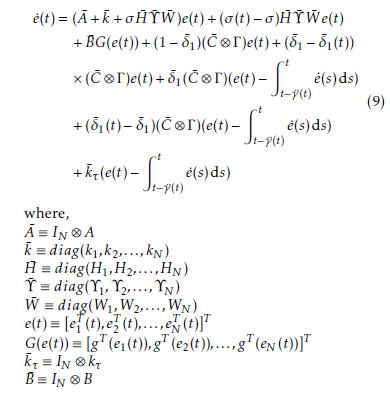
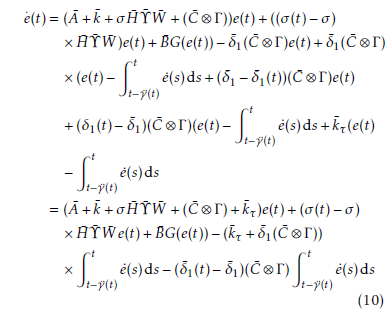3. Main results

This section establishes sufficient condition for the synchronization purposes of the CDNs. Additionally, the method for designing the synchronization controllers are presented in terms of LMIs.

Theorem 1 Suppose Assumption 1 holds. For given scalars σ ∈ [0,1], δ¯₁, γ¨₁, γ¨₂, and µ <˜ 1, the closedloop error system (10) is synchronized with controller gains k_i,k_τi(i = 1,2,…,N). If some positive definite matrices P ,S,W^ˆ ₁,W₂,Z ∈ _R^nN×nN exist and any given

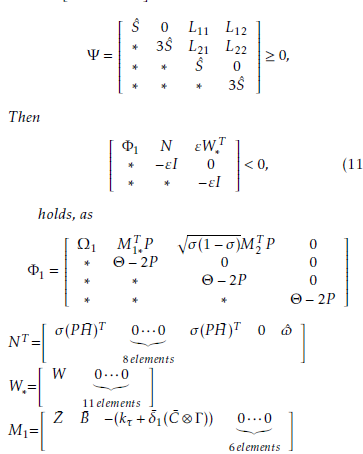
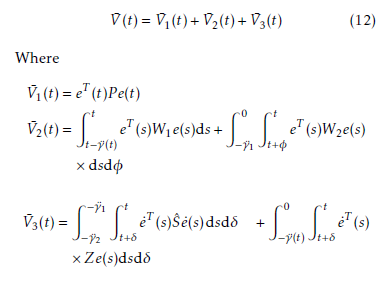Finding infinitesimal operator Ł on V¯(t) results in the following: ŁV¯(t) = lim 4^{1 {}E^{V¯(t + ⁴)^{} −} V¯(t)^}

4→₀₊

One should take note of the following expectation:

Based on Lemma (2.4), if the conclusion Φ˜ < 0 is true, then E{LV (t)} < 0. Hence, the synchronized error system is asymptotically stable. This completes the proof.

The following theorem is presented based on the above results in addressing the nonfragile control design problem.

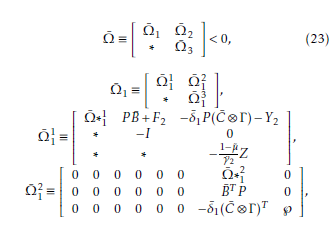
Let Y₁ = P k^¯ and Y₂ = P k^¯_τ. The control gains can be derived as k^¯ = P ⁻¹Y₁ and k^¯_τ = P ⁻¹Y₂. The proof is directly obtained from Theorem (1).

4. Numerical Simulations

The objective of this section is to exhibit the correctness of our synchronization schemes in Section (3). Example 1. The CDNs (1) is considered which comprises of five nodes with each node been two dimensional, such that N = 5 and n = 2. The other parameters involved are:

From MATLAB LMI toolbox, Theorem (2) is verified, where feasible solution of the LMIs in Theorem (2) is obtained. The controller gain matrices obtained are:

” −1.3647 K1 =        −0.1196	−0.3460 # , −1.5990
” −1.3121 K2 =        −0.0990	−0.3079 # , −1.4745
” −1.2755 K3 =        −0.0893	−0.3126 # , −1.3825
” −1.2436 K4 =        −0.0836	−0.3139 # , −1.3191
” −1.2226 K5 =        −0.0780	−0.3139 # , −1.2753
” −0.2735 K1τ =           −0.0188	−0.1907 # , −0.1500
” −0.3101 K2τ =           −0.0325	−0.1871 # , −0.2592
” −0.3163 K3τ =           −0.0335	−0.1580 # −0.3072
” −0.3192 K4τ =           −0.0292	−0.1247 # , −0.3276
” −0.3251 K5τ =           −0.0263	−0.11251 # . −0.3376

Using the following initial conditions, r˜₁(0) = [3,−1]^T , r˜₂(0) = [0,1]^T , r˜₃(0) = [−6,2]^T , r˜₄(0) = [3,−2]^T , r˜₅(0) = [−1,1]^T , and s(0) = [2,3]^T . The error trajectories (10) is shown in figure (1) without control input. The control inputs and error system trajectories with control inputs are shown in figures (2) and (3) respectively .

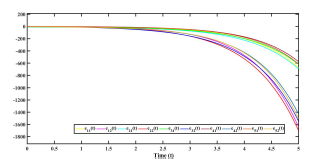Figure 1: Error synchronization without control inputs uˆ(t) in Example 1.

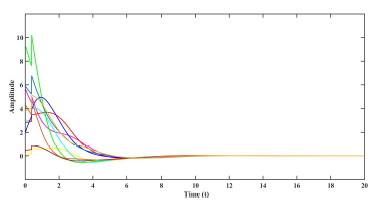Figure 2: Control inputs uˆ(t) in Example 1.

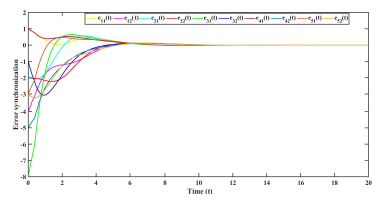Figure 3: Error synchronization with control inputs uˆ(t) in Example

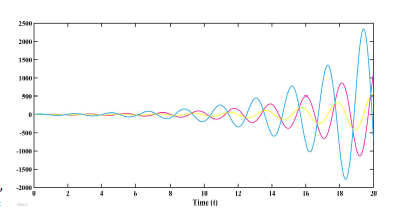Figure 4: Error synchronization without control inputs uˆ(t) in Example 2.

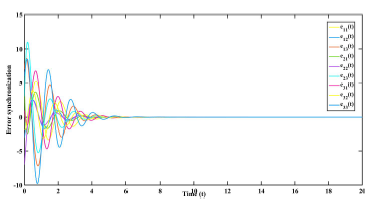Figure 5: Error synchronization with control inputs uˆ(t) in Example

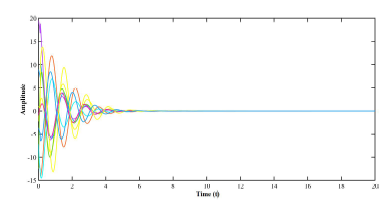Figure 6: Control inputs uˆ(t) in Example 2.

Example 2. Chua’s circuit is adopted in this example as an isolated node which is decribed by the following equation:

The obtained controller gain matrices are Assume the following initial conditions are considered for the system: s(0) = [0,−1,1]^T r˜₁(0) = [1,−2,8]^T ,r˜₂(0) = [4,−6,4]^T , and r˜₃(0) = [1,−1,7]^T . The simulation result given in figure (4) indicates state error trajectories without control input, whereas that of figures (5) and (6) depict the synchronized closed-loop error system and the control input signals respectively.

5. Conclusion

This paper shows how an appropriate Lyapunov Krasovskii functional is used to address a non fragile synchronization control problem for a stochastic coupling complex dynamical networks with time-varying delays and control gain perturbations. The application of extended version of Jensen’s inequality ensured the LMIs to be feasible. Finally, numerical examples with simulations are shown to illustrate the validity and applicability of our proposed control scheme.

Conflict of Interest

The authors declare no conflict of interest.

Acknowledgment

The authors would like to express their profound gratitude to Professor Zhong Shouming of UESTC for his immense support and contributions.

1.  F. A. Gyamfi, Y. Cheng, C. Yin and S. Zhong, Synchronization of complex dynamical networks with randomly coupling via nonfragile control, 2018 Tenth International Conference on Ubiquitonus and Future Networks (ICUFN), Prague, 2018, pp. 497 – 502.
2.  D. J. Watts and S. H. Strogatz,Collective dynamics of smallworld networks.Nature,393(6684)(1998) 440 – 442.
3.  W. Yu, G. Chen, J. L¨ u, On pinning synchronization of complex dynamical networks , Automatica 45 (2) (2009) 429 – 435.
4.  R. Rakkiyappan, G. Velmurugan, J. Nicholas George, R. Selvamani, Exponential synchronization of Lur’e complex dynamical networks with uncertain inner coupling and pinning impulsive control, Applied maths. and Comput., 307(2017) 217 – 231.
5. J. Wang, H. Zhang, Z. Wang and B. Wang, Local exponential synchronization in complex dynamical networks with time-varying and hybrid coupling,Applied Mathematics and Computation,225(2013) 16 – 32.
6. D. Li, Z. Wang and G. Ma, Controlled synchronization for complex dynamical networks with random delayed information exchanges:A non-fragile approach. Neurocomputing, 171(2016) 1047 – 1052.
7.  M. Fang, Synchronization for complex dynamical networks with time delay and discrete-time information. Applied Mathematics and Computation,258(2015) 1 – 11.
8. M. J. Park, O. M. Kwon, J. H. Park, S. M. Lee and E. J. Cha, On synchronization criterion for coupled discrete-time neural networks with interval time-varying delays. Neurocomputing, 99(2013) 188 – 196.
9.  Y. Wang, Y. Ma, A. Chen, Exponential synchronization of Markovian jump complex dynamical networks with partially uncertain transition rates and stochastic disturbances. Neurocomputing 304 (2018) 30 – 46.
10.  Y. Tang, F. Qian, H. Gao and J. Kurths, Synchronization in complex networks and its application- A survey of recent advances and challenges. Annual reviews in control 38(2) (2014) 184 – 198.
11.  A. Arenas, A. Diaz – Guilera, J. Kurths, Y. Moreno and C. Zhou, Synchronization in complex networks, Physics Reports 469 (2008) 93 – 153.
12.  M. Xu, J – L. Wang, Y – L. Huang, P – C. Wei and S – X. Wang, Pinning sychronization of complex dynamical networks with and without time-varying delay. Neurocomputing, 266(2017) 263 – 273.
13.  F. Adu – Gyamfi, Y. Cheng, C. Yin and S. Zhong, Exponential H1 synchronization of non-fragile sampled-data controlled complex dynamical networks with random coupling and time varying delay. System Science and Control Engineering, 6(1) (2018), 370 – 387.
14.  M. Syed Ali, J. Yogambigai and J. Cao, Synchronization of master-slave markovian switching complex dynamical networks with time-varying delays in nonlinear function via sliding mode control. Acta Mathematica Scientia, 37(2)(2017) 368 – 384.
15.  M. Yang, Y -W. Wang, J – W. Xiao and Y. Huang, Robust synchronization of singular complex switched networks with parameteric uncertainities and unknown coupling topologies via impulsive control. Communications in Nonlinear Science and Numerical Simulation, 17(11) (2012), 4404 – 4416.
16.  V. M. Alfaro, R. Vilanova and O. Arrieta, Fragility analysis of PID controllers. IEEE Control Applications, (CCA) Intelligent Control, (ISIC), (2009) 725-730.
17.  Y. Liu, B – Z. Guo, J. .H. Park and S – M. Lee, Nonfragile exponential synchronization of delayed complex dynamical networks with memory sampled-data control. IEEE Transactions on Neural Networks and Learning Systems. 29(1) (2018) 118 – 128.
18.  R. Zhang, D. Zeng, J. .H. Park, Y. Liu and S. Zhong, Nonfragile sampled-data synchronization for delayed complex dynamical networks with randomly occurring controller gain fluctuation. IEEE Transactions on Systems, Man and Cybernetics: Systems, 48(12)(2018) 2271 – 2281.
19.  E. Gyurkovics, K. Kiss and A. Kazemy, Non-fragile exponential synchronization of delayed complex dynamical networks with transmission delay via sampled-data control. Journal of the Franklin Institute, 355(17)(2018), 8934 – 8956.
20.  V. M. Revathi, P. Balasubramaniam and K. Ratnavelu, Delaydependent H 1 filtering for complex dynamical networks with time-varying delays in nonlinear function and network couplings. Signal Processing,118(2016) 122 – 132.
21.  X. Li and X. Fu, Effect of leakage time varying delay on stability of nonlinear differential systems. Journal of the Franklin institute, 350(6)(2012) 1335 – 1344.
22.  H. Zhang, J. Wang, Z. Wang and H. Liang, Mode-Dependent stochastic synchronization for Markovian coupled neural networks with time-varying mode-delays. IEEE Transactions on Neural Networks and Learning systems,26(11)(2015) 2621 – 2634.
23.  H. Bao, J .H. Park and J. Cao, Exponential synchronization of coupled stochastic memristor-based neural networks with time-varying probabilitic delay coupling and impulsive delay. IEEE Transactions on Neural Networks and Learning Systems, 27(1)(2015) 190 – 201.

(Click Here)

(Click Here)