1. Introduction and Preliminaries

This paper was originally published in the Conference: 2018 International Conference on Advanced Science and Engineering (ICOASE), Iraq [1]. It is well known that the concept of asymptotically nonexpansive introduced by Goebel and Kirk [2]. Additionally, every asymptotically nonexpansive map of a Banach space has a fixed point is proved. In [3], Petryshyn and Williamson proved the weak and strong convergence for quasi-nonexpansive map by using a sufficient and necessary condition. Alber [4], a new class of asymptotically nonexpansive is introduced. As well as, approximating methods for finding their fixed points are studied.   In 2014, G. S. Saluja [5] established the strong and weak convergence for approximating common fixed point for generalized asymptotically quasi-nonexpansive maps in a Banach space.

Very recently, In [6], the authors proposed an implicit iteration for two finite families of generalized asymptotically quasi-nonexpansive maps. As well as, some strong convergence theorems are established. It is useful to point out our findings in this area which appeared in [7].

Let B be a non-empty closed convex subset of a real Banach space M and T be a self-map of B. The set of all fixed points denoted by F(T). A self-map T from B into M is called nonexpansive map [2] if

and is called quasi- nonexpansive map [6] if

.

A Banach space M is satisfying:

• “Opial’s condition if for each sequence in , is weak convergence to  implies that

for all

• “Kadec-Klee property if for each sequence in  is weak convergence  to  together with  converges strongly to  imply that  is strong convergence to a point

The aim of this paper, an iterative scheme for two families of total asymptotically quasi-nonexpansive maps is established. The strong and weak convergence theorems of this scheme for approximation of common fixed points in Banach space by using suitable conditions are established. For this purpose, let us recall the following definitions and lemmas.

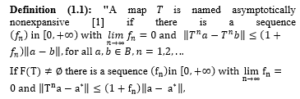
Note: Now to explain the relation between the above definitions:

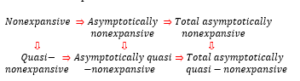
2. Main Results

Let B be a nonempty closed convex subset of a Banach space M and  be two families of total asymptotically quasi-nonexpansive self-maps. We define the iteration algorithm   as follows:

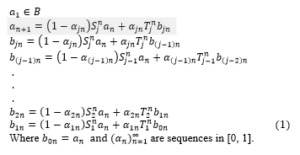
Lemma (2.2): Let  be a nonempty closed convex subset of a normed space M and  be two families of total asymptotically quasi-nonexpansive self-maps of B. Presume  be as shown in step (1). Therefore,  exists for all

Proof: By Lemma (2.1.i)

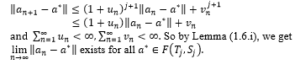
Lemma (2.3): Let  be a nonempty closed convex subset of a Banach space  and  be two families of Lipschitzain and total asymptotically quasi-nonexpansive self-maps of B. Let  be as shown in step (1). Therefore, for all  the limit

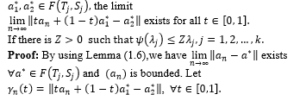
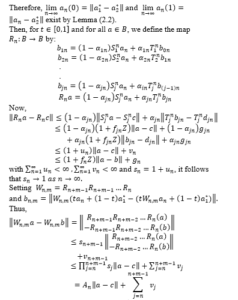
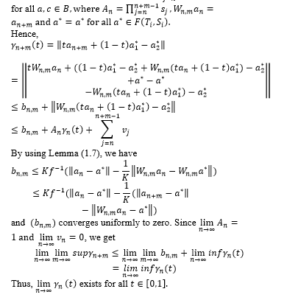
Theorem (2.4): Let  be a nonempty closed convex subset of a uniformly convex Banach space ,  be two families of Lipschiztain and total asymptotically quasi-nonexpansive self-maps of B and the sequence  be as shown

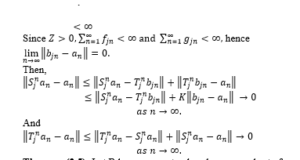
Theorem (2.5): Let B be a nonempty closed convex subset of a Banach space and  be two families of total asymptotically quasi-nonexpansive self-maps of B. Presume that  and be as shown in step (1)is strong convergence to a common fixed point of  iff

Proof: To show   implies that  is strong convergence to a common fixed point of , since by (2)

Theorem (2.6): Let B be a nonempty closed convex subset of a uniformly convex Banach space and   be two families of Lipschitzain and total asymptotically quasi-nonexpansive self-maps of B. If M accomplishes Opial’s condition and the maps  are demiclosed to zero, therefore  be as shown in step (1) is weak convergence to a common fixed point of

Theorem (2.7): Let B be a nonempty closed convex subset of a uniformly convex Banach space and  be two families of Lipschitzain and total asymptotically quasi-nonexpansive self-maps of B. If the dual space  has the Kadec-klee property and the maps  are demi-closed to zero, therefore,    be as shown in step (1) is weak convergence to a common fixed point of

Proof: As showed by Lemma (2.2), that  exists.

Since  is bounded in B and  is reflexive. Therefore, there exists a subsequence  which is weak convergence to a point . By Theorem (2.4)

The following corollaries are special cases

 

Corollary (2.8): Let  be a nonempty closed convex subset of a Banach space and  be two families of total asymptotically nonexpansive self-maps of B. Presume that  and

be as shown in step (1) is strong convergence to a a common fixed point of  iff

Corollary (2.9): Let  be as in corollary (2.8). Therefore  be as shown in step (1) is strong convergence to  iff  that converges to

Corollary (2.10): Let  be a nonempty closed convex subset of a uniformly convex Banach space and  be two families of Lipschitzain and total asymptotically nonexpansive self-maps of B. If the dual space  has the Kadec-klee property and the maps  are demi-closed to zero, therefore  be as shown in step (1) is weak convergence to a common fixed point of

Corollary (2.11): Let  be a nonempty closed convex subset of a uniformly convex Banach space and  be two families of total asymptotically nonexpansive self-maps of B. If M accomplishes Opial’s condition and the maps  are demi-closed to zero, therefore,  be as shown in step (1) is weak convergence to a common fixed point of

Corollary (2.12): Let  be a nonempty closed convex subset of a Banach space and  be two families of asymptotically quasi-nonexpansive self-maps of B. Presume that  and   be as shown in step (1) is strong convergence  to a common fixed point of  iff

Corollary (2.13): Let  be a nonempty closed convex subset of a uniformly convex Banach space and  be two families of Lipschitzain and asymptotically quasi-nonexpansive self-maps of B. If the dual space  has the Kadec-klee property and the maps  are demi-closed to zero, therefore,  be as shown in step (1) is weak convergence to a common fixed point of

Corollary (2.14): Let  be a nonempty closed convex subset of a uniformly convex Banach space and  be two families of Lipschitzain and asymptotically quasi-nonexpansive selfmaps of B. If M accomplishes Opial’s condition and the maps  are demi-closed to zero, therefore,  be as shown in step (1) is weak convergenve to a common fixed point of

3. Numerical Example

We illustrate our results by the following

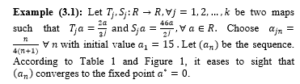
converges to the fixed point .

Table 1: Numerical results corresponding to  for 36 steps.

n	Iteration (1)	n	Iteration (1)
1	15.0000	13	0.0184
2	9.4401	14	0.0102
3	5.6594	15	0.0056
4	3.3084	16	0.0031
5	1.9044	17	0.0017
6	1.0849	18	0.0009
7	0.6134	19	0.0005
8	0.3448	20	0.0003
9	0.1930	21	0.0002
10	0.1076	22	0.0001
11	0.0599	23	0.0000
12	0.0332	24	0.0000

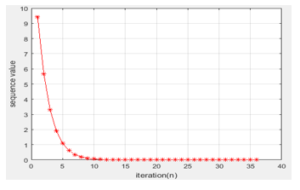
Figure. 1. Convergence behavior corresponding to  for 36 steps.

4. Conclusion

We study the strongly and weakly convergence of new type of finite-step iteration processes under total asymptotically quasi-nonexpansive maps, see Theorems (2.4)-(2.6). Our results are generalizing and unifying the results of others who have been referred to in the references.

5. Open Problem

Recently, S.S. Abed has been defined as the following type of generalizations of total asymptotically quasi-nonexpansive[16]: Let be a subset of real Banach space a set–valued map   is called the general asymptotic set-valued if for each   there exists null non- negative real sequences {a_n} and {b_n} such that

for any  ,  and  with

One can study convergence theorems in (1) and in [17, theorem (11)] for families of general asymptotic set-valued maps. As well as possible to demonstrate new results in the case of other spaces as a modular space [18].

Acknowledgment

The authors wish to express his thanks to the referees for their helpful advice.

1.  S.S.Abed, Z.M Mohamed Hasan “Convergence theorems of a finite-step iteration algorithm under two finite families of total asymptotically quasi-nonexpansive maps” IEEE Xplore Digital Library Internationl Conference on Advanced Science and Engineering (ICOASE), , 2018.
2.  U K.Goebel, W. A. Kirk, “Fixed point theorem for asymptotically nonexpansive mappings” Proc. Amer. Math. Soc. 35, 171-174, 1972.
3.  W. V. Petryshyn, T. E. Williamson, “Strong and weak convergence of the sequence of successive approximations for quasi-nonexpansive mappings”, J. Math. Anal. Appl. 43, 459-497, 1973.
4.  YA. I. Alber, C. E. Chidume, H. Zegeye, ” Approximating fixed points of total asymptotically nonexpansive mappings” Fixed point theory Appl. 2006, article ID 10673.
5.  G. S. Saluja, “Convergence to common fixed points for generalized asymptotically quasi-nonexpansive mappings” Bull. Soc. Math. 4, 69-79, 2014.
6.  G. S. Saluja, “Strong convergence theorems for two finite families of generalized asymptotically quasi-nonexpansive mappings with application” Math. Moravica, 22(1), 1-14, 2018.
7.  S.S.Abed, Z.M Mohamed Hasan,.”Common fixed point of a finite-step iteration algorithm under total asymptotically quasi-nonexpansive maps” is accepted in Baghdad Science Journal.
8.  J. B. Diaz, F. B. Metcalf, “On the structure of the set of subsequential limit points of successive approximation” Bull. Amer. Math. Soc., 73, 516–519, 1967.
9.  D. R, Sahu, D. ORegan, R. P. Agarwal ,”Fixed point theorey for Lipschitzain-type mappings with applications, Topological fixed point theory and its applications” doi:10.1007/978-387-75818-3-1.
10.  Q. H. Liu, “Iterative sequences for asymptotically quasi-nonexpansive mappings” J. Math. Anal. Appl. 259(1), 1–7, 2001.
11.  A. Abkar, M. Shekarbaigi,”A novel iteration algorithm applied to totally asymptotically nonexpansive mappings in CAT(0) spaces” Mathematices 5,14, 2017, doi:10.3390/math5010014.
12.  F.E.Browder,” Semicontractive and semiaccretive nonlinear mappings in Banach spaces” Bull. Amer. Math. Soc. 74, 660-665, 1968.
13.  A.Sharma, M.Imdad, “Approximating fixed points of generalized nonexpansive mappings Via faster iteration schemes” Fixed point theory, 4(4), 605-623, 2014.
14.  C. E. Chidume, E.U. Ofoedu, “Approximation of common fixed points for finite families of total asymptotically nonexpansive mappings” J. Math. Anal. Appl. 333, 128-141, 2007,doi:10.1016/j.jmaa.2006.09.023.
15.  J.G. Falset, W. Kaczor, T. Kuczumow, S. Reich, ” Weak convergence theorem for asymptotically nonexpansive mappings and semigroups”, Nonlinear Anal. 43, 377- 401, 2001.
16.  S.S.Abed, “Approximating fixed points of the general set –valued asymptotically mappings ” to appear.
17.  S.S.Abed, Z.M Mohamed Hasan “Convergence comparison of two schemes for common fixed points with an application” accepted in Ibn Al Haitham journal for pure and applied sciences.
18. S.S.Abed, K. E. Abdul Sada, ” Common fixed points in modular spaces”, IHSCICONF 2017, Ibn Al Haitham journal for pure and applied sciences.

(Click Here)

(Click Here)