1. Introduction

It is well-known that some type of bacteria might be lethal in humans [1] moreover in the shortest times, so that their understanding

with respect to physical and chemical interactions constitutes a must. Nowadays, notable advances to tackle down diseases caused by bacteria and virus have demanded to engineer precise pharmacology [2]. Furthermore, with the expected arrival of nanomedicine, one expects that the so-called nanodevices [3] can achieve an efficient task to defeat any intrusion of microbiological compound in humans. Thus, an accurate knowledge of bacteria’s properties and biochemical characteristics turns out to be critic for the application of an accurate nano pharmacology, with the lowest cost-benefits fraction

[4].

In this paper, theory of bacteria’s response to electrical interactions derived from both classical electrodynamics and quantum mechanics path integrals is treated. Essentially, particular attention is paid on the probability amplitude. Commonly it is written as [5],

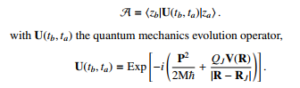
at the order of nanometer leads us to implement this approach by

which quantum effects cannot be discarded. Thus this paper has a target to present a scheme to identify bacteria through the measurement of the probability as function of time and spatial displacement. Because bacteria have a well defined ionic composition, it make them sensitive to electrical interactions. Therefore bacteria can be disturbed by electric fields and potentials, as consequence their dynamics is strongly affected. In this manner, chemotaxis and quorum among them are modified. Therefore, bacteria would exhibit patterns in according to their internal ionic composition. With this information, then is plausible their identification. The usage of quantum mechanics appears as a closed-form tool that would describe perturbed paths of bacteria. Thus, one can ask about the probability that an aggregation of bacteria is disabled in their main functions in presence of external electric fields. This paper has as purpose to answer this question.

The rest of this paper is as follows: in second section all the classic physics that would model bacteria and their spatial dynamics is presented. In third section, the implementation of the probability amplitude with the gained knowledge from the classical analysis is done. In fourth section, the implementation of integer-order Bessel’s functions is done. This has as objective to extract the possible probabilities while a single bacterium is trapped in a closed space. Finally, conclusion of paper is presented.

2. Bacteria in Classical Physics

As studied by Bechhold at 1904, bacteria are carriers of negative charges. At 1932 Leo Olitzki studied bacterial migration of cells under various values of pH [6]. After at 1932, Burke and Gibson analyzed electric reactions of bacteria observing spatial translation to the positive pole and demonstrating the negative charge composition of bacteria under fixed electrodynamic situations [7]. Therefore, it is possible to extract an exact dynamics to understand the response and behavior of bacteria or any microbiological aggregation in a scenario of electrical exposure.

Thus, by knowing the electric potential, the entire dynamics is derived from the Newton’s equation given by: F~ = Mvdv/ds =

−Q^∇~[Φ(x,y,z) + φ(x,y,z)] with φ(x,y,z) a noise that emerges in macro-biological scenarios. However in isolated environments φ(x,y,z) ≈ 0.

2.1. The Classical Dynamics Approach

Consider the Poisson’s equation defined by an electric potential U(r) and charge volumetric density ρ written as:

where the well-known Gauss’s law is used. In this manner the electric force F = qE, onto a single bacterium of charge q

due to the presence of an external total charge Q is written as

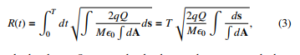
clearly the charge Q supposed to be the one that acts onto the bacterium is a finite sum of independent charges. Thus one gets:

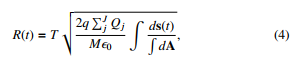
in the same logic, the displacement done by a compound of N bacteria due to the presence of Q charges is written as:

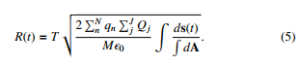
If all charges have same magnitude, then ^P_n^N q_n = Nq and ^PJ_j Q_j =

1. JQ. A toy model can be established from Eq.(5) in the sense that the net displacement for N bacteria and J external charges can be written as:

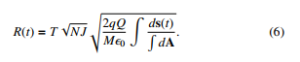
Integrations inside the square root can be carry out in a straightforward manner in according to the choice of coordinate system.

For instance a choice is the cylindric system allows us to write

R dA=2πLr(t). On the other hand while the electric force acts onto the radial direction then ds(t) → dr(t) therefore one obtains that:

 

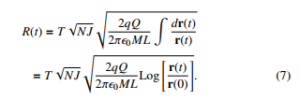
Clearly the classic physics establishes that the displacement is dictated by the inverse of the root square of product of ML. In this manner, when ML >> NJ the net displacement might be negligible.

2.2. The Electrodynamics Classical Approach

A rigorous treatment about the dynamics of any ionic compound in an electrical scenario demands to use exact solutions of either Poisson or Laplace equations. By following the picture that a single bacterium is enclosed inside a cylindric system, it is possible to derive a closed-form formulation of the bacteria displacement. In fact, consider a charged object inside a finite cylindric shape, then the electric potential becomes the Jackson’s potential [8] and it is written as:

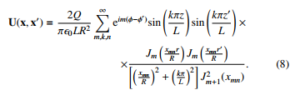
Thus, one can see that actually this full solution is the product of the individual solutions of the involved coordinates, so that one can state that the solution is separable as: U(x,x⁰) = Φ(φ,φ⁰)Z(z,z⁰)R(ρ,ρ⁰). While one can adopt the radial solution, it is explicitly dependent on the integer numbers m,k,n.

In this manner, the solution along the z coordinate appears as the one that exhibits tractability from the mathematical point of view, and that fits with the physics about the motility and spatial displacements of bacteria. Subsequently, for a fixed radius and polar angle, the Jackson’s potential can be written in its simplified form as:

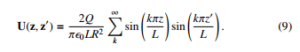
With this one can estimate the electric field from E = −∇U(z,z⁰) created along the longitudinal coordinate turns out to be:

When the difference |z − z⁰| << 1 the electric field depends on this so that the identity sin(2x)=2 sin(x)cos(x) is used. Thus, a single

bacterium containing an ion of charge q inside the cylinder feels this field and it is going to experience a net electric force given by:

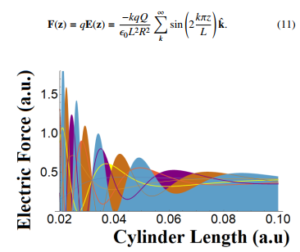
Figure 1: The intensity of electric force ||F(z)|| from Eq.(11) in the S.I system on a single bacterium as function of the length of cylinder L for values of k from 1 to 7. A noise field of 40% is attained.

3. The Probability Amplitude of Bacteria Displacement

3.1. Motivation

The prospective implementation of nano technologies through nano devices, would demand to employ accurate theoretical formulations that would have to encompass for example the nano biological scenarios. Under this view, emerges quantum mechanics as a robust theoretical frame that would describe the interactions through the language of probabilities.

In fact, commonly in quantum mechanics the probability amplitude A requires of the exact knowledge of the Green’s function or the function that dictates the space-time propagation. For example, the propagation of a massive particle from the point t_a,z_a to t_b,z_b is given by:

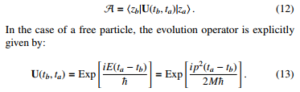
In praxis one needs to employ the representation of momentum

R given by the completeness relation               dp |pi hp| = I on gets:

In order to evaluate the integral, it is required the explicit form of the initial and final states at the momentum representation. Thus, these states can be written as Exp(−i ^pz_~^a) and Exp(i ^pz_~^b) respectively with normalization constants for both states given by √¹ , with

2π~

the causal condition t_a > t_b then the integration turns out to be in a straightforward manner resulting in (the reader can check that the square completion ”trick” is used.):

Clearly Eq.(15) requires of an additional physics that by the which one can describe the displacement of bacteria in presence of external fields. Therefore, Eq.(15) can model all those trajectories with those intensities that are negligible and cannot to affect dynamics.

3.2. The Path Integral Scheme

The scheme of path integral invented by Feynman [9] inside the framework of quantum electrodynamics [10] emerged as an independent methodology to find probability amplitudes of elementary processes.

For instance, the case subject to a negligible external potential one could be treating the free particle containing kinetic energy. Therefore, the probability amplitude contains an infinite number of paths for a spatial displacement initialized at z_b,t_b arriving to z_a,t_a. In order to calculate the amplitude probability the employed time for carrying out such motility demands to assume that the whole employed time has N+1 slices in the form: t<sub>`</sub> = ` + t_a with the integer ` running from ` = 0,1,…, N, N + 1 so that the concrete problem consists in to evaluate the product of integrals from the general formulation:

It should be noted that the kinematic part is denoted by the freeparticle Lagrangian

Turning back on the bacteria displacement, one can apply the method given above to attack the problem of bacteria motility when it is subject to external potential. In fact, Janke and Kleinert [11] have demonstrated that the path integral of a free particle between two space points inside a box is actually the product of the wellknown wave functions when these closed-form solutions of the

Schrodinger’s equation. Thus, Janke and Kleinert have found that¨ < z_b,t_b|z_a,t_a > turns out to be a closed-form expression characterized by having a complex exponential, and reads:

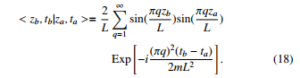
It is interesting to note that of product of two sin functions matches well to right-side of Eq.(9). In this manner, because the pres-

q

ence of the wave functions: Ψ(βz_a) =            _L²Sin(βz_a) and Ψ(βz_b) =

q

L²Sin(βz_b), with β = ^q _L^π, one can interpret that are solutions for a free particle in a cylinder. Furthermore, Eq.(18) can be also written in a simplified manner as:

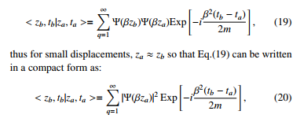
exhibiting the square of wave function denoting the probability density. With the definition of γ = _π ²0_LR^Q ₂ the Jackson’s potential from Eq.(9) can be rewritten as:

Certainly, Q denotes the charge that generates the Jackson’s potential inside and outside of cylinder of length L and radius a. Therefore, the quantum mechanics paths are contained inside the cylinder. It is noteworthy to remark that the geometry ”seen” by the charge Q is a finite cylinder.

3.3. Bacteria in a Cylindrical Geometry

Consider now a negatively charged bacteria under circumstances as given in [? ] with electric properties as studied and simulated in [? ] with charge Q_B that can move along the surface of cylinder, then the force per unit of charge attained to a single bacterium can be derived in a straightforward manner as:

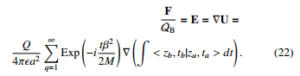
where the electric potential has been approximated to the probability amplitude. Under this assumption it is clear that Eq.(22) differs notable from the pure classic force. One can note that the quantity M and Q_B becomes the mass and charge of a single bacterium.

The infinite sum gives account of the quantum paths. Aside, the

R

term       < z_b,t_b|z_a,t_a > dt exhibits the character probabilistic since < z_b,t_b|z_a,t_a > is understood as the density of probability. It is interesting to note that from Eq.(22) the basic Coulomb force between the bacteria and test charge separated by a distance a each other can be derived, yielding:

that would indicate that bacterium and a charge Q (as nano device

for instance) are experiencing a Coulomb force each other along the quantum path (as seen at Fig.2) with a separation given by a distance a the cylinder radius.

In other words the single bacterium in a cylinder with a << L is attained to be on the cylinder surface. In this manner, the charge Q generates a Coulomb-like force to a single bacterium.

R

In addition, the gradient of the probability < z_b,t_b|z_a,t_a > dt provides the stochastic component to the dynamics of bacteria in presence of an external charge Q.

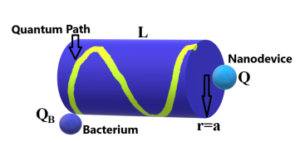
Figure 2: Sketch of the quantum path along the external area of cylinder indicating the constant radial distance between the bacterium and nanodevice.

The resulting hybrid force or semi-classical force might opt only of the real part with respect to the complex exponential, so that one gets that:

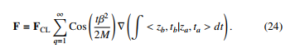
< z_b,t_b|z_a,t_a > dt is assumed to be proportional to αz that means that the probability to find the bacteria inside the cylindric geometry increases with the longitudinal distance z. Despite of this, one can see that the electric force decreases with the bacterial mass or aggregation [12].

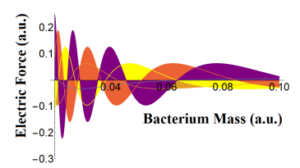
Figure 3: The electric force at the S.I as function of bacteria mass in according to Eq.(24). The force appears to be extenuated in up to a 40% of their top values as seen for a mass of 0.08 expressed in arbitrary units.

4. Bessel Shapes of Bacterium Paths

Turning back to Eq.(24), attention is paid on the complex exponential,

q2π2 where the change sin(λ) = _L2 , therefore the direct application of the expansion then reads as:

              FCL              `               2M

In Fig.4, Eq.(28) the relative force was plotted up to for 5 orders of the Bessel function. For this end z_b,t_b|z_a,t_a > dt turned out to be proportional to Cos(z_b). The dominant distribution is for ` = 1. In contrast to Fig.3, the relative force does not decreases for large values of bacterium mass. The fact that one can see small values, then it might correlated to the dominance of the classic of Coulomb force against the quantum description. It is fully coherent for large values of bacteria’s mass that exhibits a small relative force indicating that that for large masses the Coulomb force governs the electrical interactions.

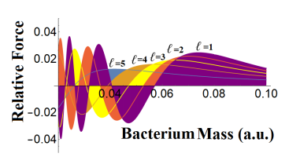
Figure 4: The relative electric force from Eq.(26) in the S.I up to for the first 5 orders of the Bessel function.

In order to include the probabilistic concept in Eq.(28) the relative force can be understood as the gradient of quantum mechanics probability in the sense of:

with P(z_b) the probability of finding a single bacterium at z_b.

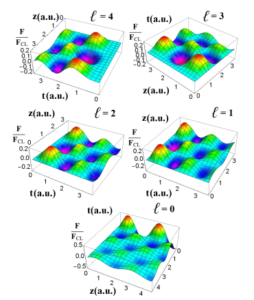
Figure 5: The relative electric force from bottom to top for the orders `=0-4 as function of space and time (expressed in arbitrary units) for a fixed value of bacterium mas M = 1.

4.1. Probabilities as Electric Patterns of Bacteria

In Fig.5 up to 5 different 3D distribution of the Eq.28 at a fixed mass, and as function of the z coordinate and time are plotted.

Since the relative force is proportional to the gradient of probability z_b,t_b|z_a,t_a > dt, then Fig.5 can be seen as the curves of probabilities.

In this sense the peaks that all surfaces are exhibiting would correspond to the best scenarios by which one can measure the mass leading to the identification of a particular specie. In bottom panel the case when `=0 is shown. One can see that at t = 0 up to 2 maximum values for z = 0.5 and 3.0 are exhibited by the 3D curve. One clearly can see that the approximation of Eq.(28) might give a better interpretation of this curve in the sense that for ` = 0 results

in F^FCL<sub>`</sub> ∇P(z<sub>b</sub>) exhibiting the important weight of the quantum mechanics probability that would be the cause for the apparition of peaks. In middle right panel, the relative force for ` = 1 displays again two peaks (both curves in color red) for t=0.1, while at the left side the case for ` = 2 again is exhibited two peaks for t=0.2. Therefore, the order of the Bessel function might be understood as the cause of a slight shift at time with a reduced relative force. This is analogue to the case of the wave packet whose amplitude is minimized with time. Therefore the relative force has actually a quantum behavior as consequence of the classical and quantum engagement through the Jackson’s potential. However, the degradation of these surfaces of probabilities are balanced with the apparition of minor peaks as seen at left and right plots. In top left plot, the case when ` = 3 is plotted. Here there are two peaks at t = 1.5 at z = 1 and z = 3.5. It is noteworthy as done in previous case, one can see the apparition of minor peaks. Again, the variation as to up and down of the relative force is entirely related to the quantum behavior. The drastic case is seen at the left panel where ` = 4 whose peaks appear to be rather reduced in contrast to previous cases. In effect, at t = 2 and z = 2.5 is seen a hole resulting in a null probability and the electric interaction with a nano device [13] inside the cylinder is either lost or not enough to measure the tracking of bacterium under the assumption that there multiple paths that bacterium would opt while is inside of a closed geometry.

5. Conclusion

In this paper, the analysis of any microscopic biological specie such as a single bacterium or virus containing a ionic aggregation inside, has been treated through classical and quantum methodologies. The results, have shown that the path integral formulation might enclose the classical electrodynamics formulation dictated by the Jackson’s potential. Thus, the relative force was defined as the ratio of the quantum mechanics over the Coulomb-like under the assumption that an engineered nano device [14] coexist inside the cylinder. The 3D plots (done with the package Wolfram [15] for figures 1-5) for different orders of Bessel function have exhibited that the bacterium acquires a pure quantum mechanics behavior. Further studies to understand this quantum and classical correspondence in a more general view are required to support the diverse transitions between the classical and quantum mechanics in nano systems subject to classical fields.

1. A. F. Boggs, “Antibacterial resistance: who pays?” Expert Opinion on Thera- peutic Patents, 13(8), 1107–1112, 2005, doi:10.1517/13543776.13.8.1107.
2. L. Good, “Antisense antibacterials,” Expert Opinion on Therapeutic Patents, 12(8), 1173–1179, 2002, doi:10.1517/13543776.12.8.1173.
3. H. Nieto-Chaupis, “Macrophage-Like Nanorobots To Anticipate Bacterial Dynamics,” in 2019 IEEE 9th Annual Computing and Communication Work- shop and Conference (CCWC), 0873–08789, 2019, doi:10.1109/CCWC.2019. 8666506.
4. H. Nieto-Chaupis, “Bacteria Nano Communications Described by a Machine Learning Theory Based on the Feynman Path Integral,” in 2019 IEEE 53th Annual Conference on Information Sciences and Systems (CISS), 1–4, 2019, doi:10.1109/CISS.2019.8692893.
5. J. J. Sakurai, Modern Quantum Mechanics, Chapter II Section 2.5, Addison- Wesley, 2010.
6. L. Olitzki, “Electrical Charge of Bacterial Antigens,” The Journal of Immunol- ogy, 4, 251–256, 1932, doi:10.1186/s11671-019-3005-z.
7. V. Burke, F. O. Gibson, “The Gram Reaction and the Electric Charge of Bacteria,” The Journal of Immunology, 2, 211–214, 1932, doi:10.1186/ s11671-019-3005-z.
8. J. D. Jackson, Classical Electrodynamics, Third Edition, Chapter II, Problem 3.13, Wiley, 1999.
9. R. P. Feynman, “Space-Time Approach to Quantum Electrodynamics,” Physi- cal Review, 76, 769, 1949, doi:10.1103/PhysRev.76.769.
10. R. P. Feynman, “Mathematical Formulation of the Quantum Theory of Electro- magnetic Interaction,” Physical Review, 80, 440, 1950, doi:10.1103/PhysRev. 80.440.
11. W. Janke, H. Kleinert, “Summing Paths for a Particle in a Box,” Lettere Nuovo Cimento, 25, 297–300, 1979, doi:10.1007/BF02776259.
12. M. M.-H. Hasnaa Fatehi, M. T. Figge, “Modelling cellular aggregation in- duced by chemotaxis and phototaxis,” Mathematical Medicine and Biology: A Journal of the IMA, 373–384, doi:10.1093/imammb/dqq002.
13. Y. W. Mingyu Wang, Z. Yang, “Cooperation Method of Symmetrically Dis- tributed Multi-Nanorobotic Manipulators Inside SEM for Nanodevice Constructing,” in 2018 IEEE 13th Annual International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), 543–548, 2018, doi:10.1109/ NEMS.2018.855.6984.
14. Q. Xia, “Memristive nanodevices: CMOS compatibility and novel applications,” in 2016 IEEE 18th Mediterranean Electrotechnical Conference (MELECON), 1–4, 2016, doi:10.1109/MELCON.2016.7495316.
15. “Wolfram Mathematica https://www.wolfram.com,” .

(Click Here)

(Click Here)