1. Introduction

Hamming distance between arbitrary binary vectors is determined by the number of binary digits in which the compared vectors do not match [1]. This distance is often used to assess the proximity of discrete objects, which are described using binary alphabets with binary {0, 1} or bipolar {–1, 1} components. On the basis of bipolar neurons, a discrete Hamming neural network has been developed [1], which is successfully used to solve problems of recognition and the proximity measure of binary objects, the components of which are encoded using alphabet elements {–1, 1}, estimation. However, the evaluation of the measure of proximity of the compared objects (binary bipolar vectors) is carried out only by the most noticeable signs – different binary digits. At the same time, more “subtle” features for compared objects are ignored, which are often used to assess the similarity of binary vectors using the affinity (similarity) functions of Russell and Rao, Dice, Kulchitsky, Yule, etc.

In particular, in works [2–5] a brief description of these functions and their application is provided to compare different objects. In studies [2] they are used in the development of artificial immune systems, in works [3] and [4] they are used in the development of recognition systems for various objects. In this case, the characteristics of such objects are encoded by binary features. In work [5] given function is used to classify microorganisms.

In works [2–5], it is described and used not more than 15 commonly used functions. Although their total number is noticeably higher. So, in research in mathematical biology [6], 20 functions are used, and with hierarchical clustering, the set of random binary data (Hierarchical clustering Result of Random Binary Data Set) 76 different functions are indicated [7]. Once again it indicates the relevance of the application of this approach for the classification and assessment of the proximity of various objects, which is described by a plurality of binary features.

2. Problem Statement

The template is used to format your paper and style the text. All margins, column widths, line spaces, and text fonts are prescribed; please do not alter them. You may note peculiarities. For example, the head margin in this template measures proportionately more than is customary. This measurement and others are deliberate, using specifications that anticipate your paper as one part of the entire proceedings, and not as an independent document. Please do not revise any of the current designations.

Analysis of recent publications on the theory and application of neural network Hamming [1 – 10] shows that the Hamming network has distinct disadvantages. In the architecture of the Hemming neural network, highly specialized layers of neurons are used: neuron layer calculating only the dot product of binary bipolar vectors; a neural network that allows you to select only one reference image from the network memory. This image is at the minimum distance from the input image in connection with this network

– It cannot work with the binary input data, when the measure of proximity of objects is estimated using finer characteristics than the Hamming distance. In particular, using the distances [2 – 5, 7];

– It cannot recognize objects, if they are at the same minimum distance from the two or more reference objects [1];

– cannot switch from processing information encoded using a bipolar alphabet to processing information presented using a binary alphabet and vice versa.

All this requires the development of a new Hemming neural network with a more advanced architecture.

When comparing objects with qualitative features encoded using a binary alphabet, for each pair of objects (binary vectors)  in works [2 –5] four variable: a, b, f, g are used (table 1).

The variable a is used to count the number of bits with coinciding unit components of the vectors J_p and J_q. The variable b is needed to determine the number of binary digits of vectors   J_p and J_q., in which both vectors have zero components, at the same time that means these objects do not have encoded with zeros in the same bits features.

The number of unit components that an object (vector) J_p  has, but vector J_q. does not have, is determined using the variable f.  The variable g, on the contrary, counts the number of unit components that the vector J_q. has, but are absent in the second vector J_p.

From the analysis of the Table. 1 it follows that an increase in the variable a unambiguously indicates an increase in the similarity (affinity) of the compared vectors. There is no such unambiguity with an increase in the variable b, since an increase in this variable can indicate both an increase in the similarity of the compared objects, and their belonging to different classes (if there is no similarity in the variable a). As for the measure of proximity of vectors J_p and J_q with respect to the variables f and g, it is symmetric with respect to these variables. An increase of these variables indicates the differences between the compared vectors increase.

Table 1: Variables for comparing binary vectors with binary components

	Jp
Jq	1	0
1
0

Variables a, b, f and g from Table 1 are used in a number of well-known binary object similarity functions, in which the presence or absence of features is determined by the components of the binary alphabet. As an example, we can note the affinity (similarity) functions of Sokal and Michener, Jaccard and Needham, and so on. Using the variables f and g, one can easily determine the Hamming distance between binary vectors  J_p and J_q

Variables a, b, f and g, as well as the affinity functions of Sokal, Michener, Jaccard, Needman, Hamming distance can be calculated using a new neural network based on binary neurons. The disadvantage of this neural network is the impossibility of processing information presented using the bipolar alphabet, as well as the inability to calculate the Hamming distance using the above affinity functions of Sokal and Michener, Jaccard, etc.

3. Generalized Block Diagram of a Hamming Neural Network

Since the theory, architecture and algorithms for the functioning of the Hamming network are described in detail in modern literature [1, 6 – 10], we will give only a generalized block diagram of the neural network (Figure 1) and a brief description of its functioning.

In the Hamming neural network, the input image  is fed to the inputs of X-neurons, which are multipliers of the bipolar image components  Each Z-neuron stores one of the m reference images in the scales of its relations ,  and compares this image with the input . As a measure of the similarity of the compared images (bipolar vectors), their scalar product is used [1, 8]

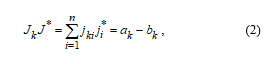
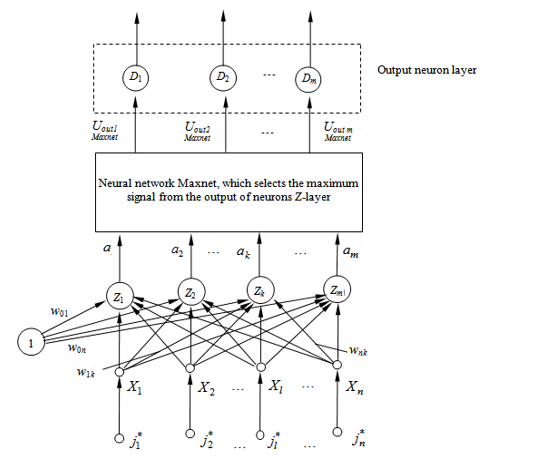Figure 1: Block diagram of the Hamming neural network

where a_k and b_k are, respectively, the number of identical and different components of the compared vectors (images)  and J^*.

Since a_k + b_k = n, the scalar product (2) can be written in the form

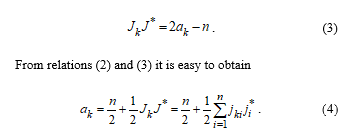Relation (4) can be regarded as a description of the input signal of a neuron  (Figure 1), which has a displacement of n/2 and n inputs, that perceive the components of the input image   through neurons  ( ). In this case, the output signals of the X-layer elements repeat their input signals:

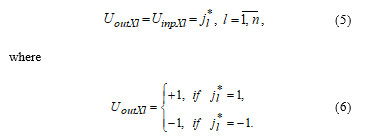Each element of the X-layer is associated with the input of each neuron of the Z-layer. The scales of these relations contain information about m reference images , stored in the neural network. The scales of relations  contain information about the k-th reference image .

Z-layer elements compute their output signals

where – function of activation of neurons of the Z-layer;  – output element’s  signal, that arrives at the input of the neuron of the Maxnet network [1, 8]. From the output signals of the Z-layer elements, the Maxnet neural network, using an iterative process, extracts a single maximum signal greater than zero. Since the output signals of D-layer neurons are calculated by the ratio

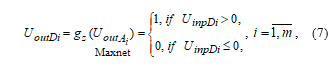then at the output of the Z-layer of D-elements there will be only one single signal, which indicates which reference image is closest to the input vector .

Analysis of the architecture of the discrete neural network shown in Figure 1 shows, that the layers of the network elements function relatively independently of each other. In particular, the layer of Z-neurons that determine the similarity functions of the input and reference images using the dot product can be replaced by blocks or neurons that calculate the similarity functions using other relations. In particular, the input bipolar signals and neurons of the X– and Z-layers can be replaced with binary.

The relative independence of the functioning of the main layers of the Hamming neural network from each other makes it possible to propose the use of binary neurons in the first layer of the network to work with binary input images (vectors). And also, to propose more “subtle” comparisons of input and stored in memory images using a variety of similarity (affinity) functions, modified using the Hamming distance (1) .

The purpose of the article is to develop a generalized architecture of the Hemming neural network, which allows you to process input information that can be specified using both bipolar and binary alphabets. Also, based on the new architecture, the development of methods for solving problems of recognition and classification of binary objects is shown. In this case, the Hamming distance is used, as well as the functions of Jaccard, Sokal and Misher, Kulchinsky, etc.

4. Analytical Relationships Connecting Similarity Functions for Binary Objects and Hamming Distance

Since similarity functions for binary vectors (objects) and for objects described using the bipolar alphabet are used to assess the similarity of binary objects, then there should be dependencies connecting the similarity functions for binary objects (vectors) and the Hamming distance. Table 2 shows the aforementioned classical affinity functions (first column of Table 2) and similarity functions, modified using the Hamming distance (second column of Table 2).

      Simple analytical relationships for determining the Hamming distance through the classic similarity functions Russel and Rao,

Table 2: Relationship between Hamming Distance and Similarity Functions for Binary Objects

Classic similarity functions	Similarity functions using Hamming distance	Hamming distance expressed in terms of binary similarity functions
Russell and Rao similarity function
Sokal and Michener similarity function
Jaccard and Needham similarity function
Kulchitsky similarity function
Dice similarity function
Yule affinity function	Bulky expression
Correlation	Bulky expression

Table 3: The Values of the Similarity Functions for the Compared Binary Vectors

	a	b	f	G	S1	S2	S3	S4	S5	S6	S7	RX
Values of similarity functions for vectors J1 and Jk	5	5	2	0	5/12	10/12	5/7	5/2	5/12	1	5/Ö35	2
Values of similarity functions for equal vectors J1 = Jk	7	5	0	0	7/12	1	1	¥	5/12	1	1	0
Numerical values of similarity functions for vectors J1 and Jk with opposite components	0	0	7	5	0	0	0	0	0	– 1	1	12

Sokal and Michener, Jaccard and Needham, Kulchitsky, Dice were shown in the third column of the Table 2 for the first time ever. It was not possible to obtain simple analytical dependences connecting the Yule similarity function  and the correlation coefficient . But it is possible to determine the Hamming distance by functions  and  can using the relation (1).

Example. Let’s perform the comparison using functions a, b, f and g,  –  some vector’s pairs:

1) J₁ = (111001110001), J_k = (101001100001);

J₁ = J_k = (111001110001);

J₁ = (111001110001); J_k = (000110001110).

The calculation results are shown in Table 3.

Analysis of the calculation results shown in Table 3 shows that the similarity functions S₁ – S₅ depend on the compared vectors. The values of these functions for vectors with opposite components take the minimum values, and for vectors with the same components, on the contrary, the maximum values.

If the compared vectors  and  do not all coincide and not all are opposite in their components, then the similarity functions S₁ – S₅ take their values between the data of the second and third rows of Table 3, that is, between its maximum and minimum values. The function S6 practically obeys this rule, and the calculated values of which, given in the first and second lines, coincide.

As follows from the data Table 3 and the third column of the Table 2, the Hamming distance in comparison with the similarity functions S₁ – S₅ behaves in a certain sense opposite: using the functions S₁ – S₆ the similarity of the compared objects (vectors) is calculated, and using the Hamming distance, on the contrary, the difference of objects (vectors), therefore the Hamming distance  takes the maximum value for vectors that do not have any of the same components and the minimum distance (equal to zero) for vectors in which all components are the same.

The affinity functions are not limited to the ratios given in Table 2 [2 – 5]. A significant number of these similarity functions indicate the absence of one universal function suitable for comparing any binary objects with binary information encoding. The choice of one similarity function for solving a specific problem is determined, as a rule, by repeated modeling on the initial data in the space of features encoded using a binary alphabet.

5. New Neural Networks that Recognize Binary Images with Binary Components

The generalized block diagram of the Hamming neural network in Figure 1 clearly shows that the three main layers of a neural network can change and function almost independently of each other. In particular, instead of the Maxnet network, another neural network can be used that selects one or several identical maximum signals (if any). This allows you to find reference images that can be at the same minimum distance from the input. It also follows from the network architecture (Figure 1) that the layer calculating the measure of proximity of the input and reference images can calculate various measures of proximity. The relative independence of the main layers of the Hamming neural network makes it possible to propose neural networks for working with binary images (vectors) and using various affinity functions given in Table. 2, between the input and reference binary images. The Hamming distance can also be used (1). The classical architecture of the Hamming neural network [1, 6] for calculating the closeness measure of the input and reference vectors involves the use of the scalar product of two bipolar vectors [1, 8], one of which is a vector of connection scales, and the other is an input vector. In this case, the sum of the products of bipolar components does not contain any zero terms. If the scalar product of two binary vectors J_q  and J_p is calculated in the classical Hamming neural network, then it is calculated as follows

where variables (a, b, f, g) are defined by relations from Table 1.

Thus, if only one neuron is required to calculate the scalar product of two bipolar vectors using a classical neural network, then to calculate the scalar product of two binary vectors, you must first calculate the variables a, b, f and g using the relations given in Table 1.

In Figure 2 a block for calculating the variable b from Table 1 via neuron Z is shown:

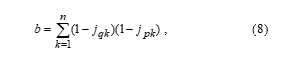where  – scales of neuron relations; ,  – neuron Z input vector components; n – number of neuron relations scales Z.

With the help of neurons å1, å2, ¼, ån  the components , , ¼,  of the input vector for neuron Z are computed. These components are accordingly communicated with the scales    ¼, , which allows us to calculate the variable b.

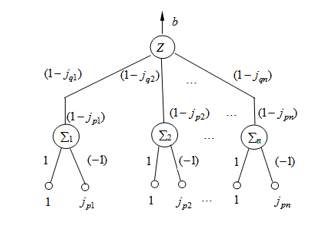Figure 2: Neuron to calculate a variable

If in Figure 2 to the inputs of neuron Z to apply input signals    ¼,  instead of signals calculated by summing elements å₁, å₂, ¼, å_n  of signals    ¼,  then neuron Z will calculate the variable f. To calculate the variable g (see Table 1) in Figure 2 it is necessary to replace the scale coefficients    ¼,  with the corresponding scale coefficients    ¼, .

To obtain from the neural network shown in Figure 2, the neural network calculating the variable a needs to leave only one neuron Z with relation scales    ¼, , to the inputs of which these    ¼,  signals, respectively have to be sent.

Having neurons or neural components for calculating the variables a, b, f and g, using table. 2 easy to get neural network architectures to compute any affinity function like Dice function  (Figure 3).

The neural network for calculating the affinity function  of the input vector and the reference vector is shown in Figure 3. The network has three layers of neurons. On the first layer of the network, the functions a, f and g are calculated. On the second layer, based on the calculated functions a, f and g, the sum 2a + f + g is calculated, which is used by the division unit to calculate the similarity function .

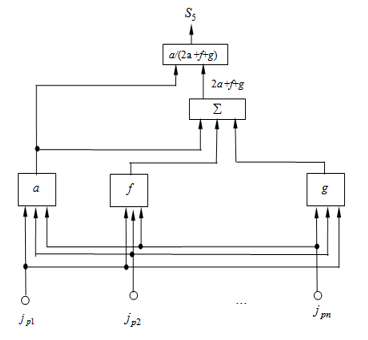Figure 3: A neural network calculating the Dice function

Similarly, neural network architecture can be obtained for calculating any other affinity functions. Figure 4 shows the architecture of a neural network that calculates the correlation coefficient , the formula for calculating which is given in the very bottom line of the table. 2. With the help of this coefficient the similarity of the input vector and the reference vector, stored in the memory of the neural network, is estimated.

The neural network (Figure 4) for calculating the correlation coefficient has six layers of neurons. On the first layer, using blocks of neurons 1 – 4, functions a, b, f and g are calculated, which on the second layer are used to calculate intermediate variables ab, (a + f) (a + g), (b + f), (b + g), fg using blocks 5 – 10. On the third network layer (fig. 4) for calculating intermediate variables (a + f) (a + g) and (b + f) (b + g) the results of calculations, respectively, of blocks 6, 7, 8 and 9 are used. On the fourth network layer, the intermediate variables of the third network layer are used to calculate the radical expression in the denominator of the correlation coefficient formula (Table 2). The fifth layer of the neural network is required to determine the numerator and denominator of the correlation coefficient , which is calculated on the last layer of the neural network.

5.1. Binary Neural Networks with the Transformation of Input InformationRrepresented Using the Bipolar Alphabet.

The architecture of neural networks for determining the Dice  function and the correlation coefficient , as well as other similarity functions, given in Table 2, in the general case can be represented in the following form (Figure 5).

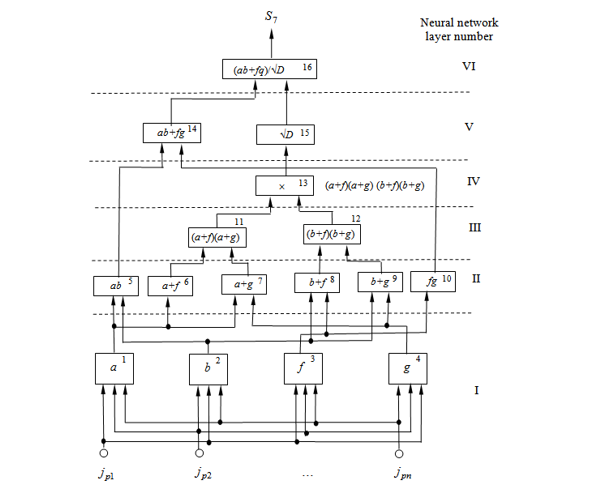Figure 4: Neural network for calculating the correlation coefficient  (the formula for calculating the coefficient  is given in the bottom line of the Table. 2)

The neural network shown in Figure 5 has four layers of neurons. Both binary and bipolar signal vectors can be applied to the network input (B-neuron layer). If binary signals    ¼, are fed to the input of the neural network, then all bipolar components of the vector (    ¼, ) are equal to zero. If nonzero bipolar components are fed to the network input, then all components of the input vector ( , , ¼, ) are equal to zero. When specifying input information using a binary alphabet, the first three layers of neurons are used in the function. In this case, the input vector of binary signals ( , , ¼, ) arrives at the first inputs of neurons B₁, B₂, ¼, B_n. Second inputs of B-neuron layer are connected to the outputs of the neuron layer, which converts the input bipolar signals ,  to binary , .

Since the input information to the network defining the similarity function comes in binary form, the input vector ( , , ¼, ) has to have all zero components. In this regard, zero signals  =  = ¼ =  = 0 also appear at the output of layer 4 of the neural network. Therefore, the second inputs of neurons B₁, B₂, ¼, B_n will receive zero signals from the outputs of the elements of layer 4. B-layer neurons have activation functions of the form

where ,  – respectively, the output and input signals of the neurons of the B-layer. In this regard, the output signals of the neurons of layer B repeat the input signals of the neural network , , ¼,  and are used to calculate the variables a, b, f and g on the second layer of the neural network, which are necessary to determine a specific similarity function .

If the input information at the inputs of the neural network shown in Fig. 5, comes in the form of a bipolar vector , , ¼, , then the neurons of layer 4 convert bipolar signals into binary according to the ratio

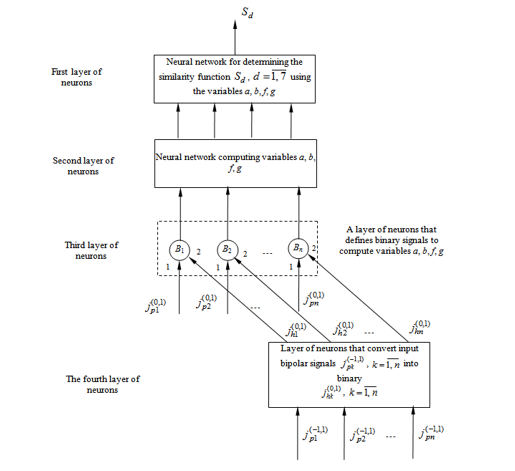Figure 5: Architecture of neural networks for determining similarity functions  –  when the input information using binary or bipolar alphabets is specified

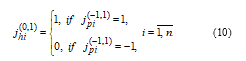The signals , , ¼,  from the outputs of the neurons of layer 4 arrive at the second inputs of neurons B₁, B₂, ¼, B_n , the first inputs of which receive zero signals , , ¼, , since the information necessary to determine the similarity function, in this case, is set in bipolar vector ( , , ¼, ).

Thus, the architecture of the neural network shown in Figure 5, provides the computation of similarity functions for both binary and bipolar input signals. Obviously, a block of neurons can be synthesized in a similar way, which transforms input information from a binary alphabet into a bipolar one.

Similar blocks for transforming input information from one alphabet to another can be used at the inputs of any neural networks.

6. Conclusions

Binary and bipolar alphabets are used in various information technologies and methods for solving problems of recognition, classification, and estimation of the proximity of various binary objects. However, there is certain isolation in the application of methods based on different alphabets. The estimation of the measure of proximity of the compared bipolar vectors (objects, images) is mainly carried out using the dot product of vectors or Hamming distance. On their basis, the Hamming neural network has been developed and widely used. However, the Hamming neural network cannot be used when the recognition problem can have several solutions, to solve problems in cases where the components of binary vectors or images are encoded using a binary alphabet. It cannot be used to estimate the affinity of binary vectors using the functions of Jaccard, Sokal and Michener, Kulchitsky, etc. In this regard, based on the generalization of the architecture of the Hamming network, new neural networks have been developed using binary coding of input information and the above similarity functions for binary objects. This expands the area of application of neural networks for solving problems of recognition and classification of input information using proximity functions using more “subtle” signs of proximity of discrete objects with binary coding. At the same time, when describing the general architecture of the generalized Hemming neural network, it is noted that the Maxnet network can be replaced by a neural network that allows you to define several solutions (if they exist). This allows, if necessary, to synthesize neural networks that allow obtaining a predetermined number of solutions in advance.

The idea of developing blocks for converting input information from one binary alphabet to another made it possible to propose not only a generalized Hamming network working with input information encoded using both binary and bipolar alphabets, but also modifications of any other binary neural networks that have worked so far with input information encoded with just one binary alphabet.

Thus, the scientific novelty of the results obtained is as follows.

For the first time, on the basis of the Hamming neural network, is proposed the concept of constructing new neural networks for solving problems of classification and recognition of binary objects using different distances and proximity functions. In doing so, the following principles are used:

1) adaptation of the first layer of neurons that determine the similarity functions of the input and reference images depending on the applied distances. This has allowed to develop a unified approach to the synthesis of neural networks that use different similarity function;

2) replacement Maxnet neural network in a neural network that can allocate one or more identical maximum signal. This allows you to select one or more reference images that are at the same minimum distance from the input image.

Also for the first time obtained the architecture and algorithms of functioning the neural network that can process the input information provided by both the bipolar and in binary form.

In real conditions some uncertainties while specific features comparison can be arisen with the binary objects’ juxtaposition. For example, while the fruits or plants juxtaposition the color can be changed in different time intervals. In this case there could be uncertainties, that will be described with the third truth state.

Wherein, the third truth value could be interpretated in different ways [11 – 14]:

– like the intermediate value between truth and false;

– like the lack of information;

– like a specific paradoxical or even meaningless value, that gives such a meaningless value too;

– like values of three-valued paraconsistent logics, in which the third truth value can be interpreted in some statements as both true and false at the same time;

– like uncertainty of the three-valued logics, that describes quantum mechanics interpretations, etc.

The theory of making solutions’ development in conditions of binary objects is a promising direction in our opinion.

Conflict of Interest

There is no conflict of interest reported between the authors.

1. V.D. Dmitrienko et al., Neural networks: architecture, algorithms and usage. Tutorial, Kharkiv, NTU “Khpi”, 222, 2020.
2. S.A. Babichev, Theoretical and practical principles of information technology for processing gene expression profiles for gene network reconstruction. Dissertation for the degree of Doctor of Technical Sciences in specialty 05.13.06 – Information Technology, Kherson, Kherson National Technical University, 382, 2018.
3. V.D. Dmitrienko et al., Methods and algorithms of artificial intelligence systems, Kiev, Kafedra, 282, 2014.
4. A. For, Perception and pattern recognition, Moscow, Engineering, 272, 1989.
5. R.S. Michalski A recent advance in data analysis: clustering jbjects into classes characterized by conjunctive concepts, Invited chapter in the book Progress in Pattern Recognition. 1, North-Holland Publishing Company, Amsterdam-NewYork-Oxford, 33-49, 1981.
6. Z. Chay et al., “Russel and Rao Coefficient is a Suitable Substitute for Dice Coefficient in Studying Restriction Mapped Genetic Distances of Escherichia colis”. – iConcept Pocket Journal Series: Computational and Mathematical Biology, January 2010.
7. S. Choi et al., “A Survey of Binary Similarity and Distance Measures”, Systemics, Cybernetics and Informatics, 8(1), 43-48, 2010.
8. V.D. Dmitrienko et al., “Neural networks for determining affinity functions”, 2020 International Congress on Human-Computer Interaction, Optimization and Robotic Applications (HORA), Ankara, Turkey, 1-5, 2020, doi: 10.1109/HORA49412.2020.9152830.
9. L.S. Yampolsky, Neurotechnology and neurosystems, Kiev, Monograph, “Dorado-Printing”, 508, 2015.
10. L. Fausett, Fundamentals of Neural Networks: Architectures, Algorithms and Applications, New Jersey: Prientice Hall. Int., 483, 2006.
11. N. Tomova, “The emergence of three-valued logics: logical and philosophical analysis”, Bulletin of Moscow University. Series 7. Philosophy, Moskow, MSU, 68-74, 2009.
12. A.S. Karpenko, Development of multi-valued logic, Ed. 3-ht, Moskow, Publishing house LCI, 448, 2010.
13. A.S. Karpenko, “Bochvar’s three-valued logic and literal paralogics”, RAS, Institute of Philosophy, Moskow, IF RAS, 110, 2016.
14. N.E. Tomova, “Natural three-valued logocs and classical logic”, Logical Investigations, 19, 344-352, 2013.

(Click Here)