1. Introduction

According to general relativity, the observed gravitational effect results from the curvature of spacetime [1]. In 1919, the deflection of light was measured and found to be as predicted by general relativity: gravitation from stars bends the paths of light rays. A tiny shift in light rays around the Sun was observed during a total solar eclipse [2].

In 1959, Pound and Rebka reported the first successful measurement of the gravitational redshift, which is a phenomenon in which the wavelength of a photon shifts to a longer wavelength when the photon moves upward against a gravitational field [3, 4]. These and other experimental results have confirmed the existence of gravitational time dilation. Many experiments verified the existence of gravitational time dilation and gravitational light-bending.

General relativity describes gravitational spacetime using tensors. Between about 1960 and the mid-1980s a variety of modifications to special relativity have been proposed, including scalartensor theories [5], vector-tensor theories [6], and tensor-vectorscalar theories [7]. A number of physicists have invented alternative theories, such as the Dickie framework and the parameterized postNewtonian formalism [5, 8, 9].

Recently, string theory has established a connection between the microscopic world of high-energy particles and the large-scale world of gravitation [2]. Physicists have also proposed a number of models to describe mass [10]–[15].

Instead of using tensors, this paper utilizes the refraction principle of Snell-Descartes to investigate gravitation from the particle level to the cosmic scale.

The refractional trajectory of light is the shortest path that is equivalent to the geodesic in a curved space. These two methods describe the same thing, but the former uses calculus, and the latter uses tensor calculus.

A ray of light changes its direction when it passes from one to another medium because the speed of the light changes in different media. This phenomenon is called refraction [16]. In gravitational time dilation, the distance that light travels changes across gradually changing spacetime. This change also results in refraction by gravitation.

Several works [17, 18] have described light-bending around a mass using the refraction mechanism, but this paper extends it to a complete derivation of Newtonian gravitation from the level of the particle using the refraction principle.

The presented derivation provides us a clear understanding of where the gravitation originated, how particles participate in creating gravitation and respond to gravitation, why all composite bodies in a gravitational field have the same acceleration, and why a particle acts like being massless.

Classical physics is applicable only to a flat space. Modern physics has extended the space and time into a spacetime curvature during a century. However, general relativity makes the mistake of including a part of classical physics, and fails to describe a steep curvature of spacetime. The Section 3.3 describes this in detail. To avoid this mistake, this paper simply utilizes only the refraction principle, Lorentz invariance, and two proposed postulates. This paper presents a new metric to describe a steep spacetime curvature, and compares it with the prior one.

2. Overview

In string theory, particles consist of one-dimensional objects called strings. We assume the following: (Postulate 1) The photon is a straight open string as a particle. All strings flow with the speed of light like the photon does, but the strings of the other particles flow within their geometric space. The strings flow in various directions depending on their geometry.

When multiple particles are chained together to comprise a nucleus, their geometric orientations are restrained, and they flow to various directions in their restrained space. When particles are linked with each other to form a nucleus, statistically a set of strings flow in every direction. Newtonian gravitation is obtained from the statistically omnidirectional flows of strings.

There is no specific boson for gravitation. All of the particles consist of strings and participate in creating gravitation, and respond to gravitation. Hence, all composite bodies in a gravitational field have the same acceleration [19]. However, a free and stationary particle can exhibit imperfect omnidirectional movement, taking a preferred orientation to minimize gravitational force, and in this case it has a different acceleration that described by Newtonian gravitation. In addition, a specific shape of particle can act like being massless.

Figure 1 shows the omnidirectional flows of a string across spacetime layers. The lower space layer has greater time dilation than the upper one according to the gravitational time dilation. The velocity of the string is constant across space layers, according to the Lorentz invariance, but time is slower in the lower space. Thus, the distance traveled in the lower space layer is shorter than in the upper one for the same coordinate time.

Strings experience refraction like a ray of light as it passes from one medium to another medium, changing its direction. Refraction was experimentally and theoretically established by the Snell-Descartes law four hundred years ago.

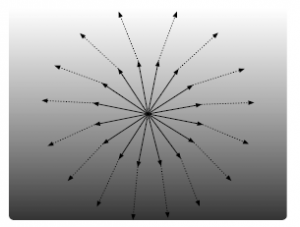
Figure 1: Omnidirectional movements and their refraction across space layers with different time dilations.

The speed of light is slower in water than in air, thus the distance traveled is shorter in water. In a similar way, time is slower in the lower space thus the distance traveled is shorter in the lower space. The re-fractional trajectory of light is the shortest path that is equivalent to the geodesic in a curved space.

Kinetic energy and thermal energy can also refracted by gravitation, because the trajectory of movement depends on the shortest path.

Refractions are illustrated as dotted lines in Figure 1. At the first time, the central velocity of the particle is zero. A short time later, the particle experiences refraction and the sum of the changes of the vertical distance for every direction heads for the center of gravitation. This refraction results in the gravitational acceleration.

This paper presents a derivation of Newtonian gravitation from the refractions of omnidirectional flows across gradually changing spacetime.

3. Derivation

This section shows the process for deriving for Newtonian gravitation from refraction by gravitational time dilation.

3.1        Refraction

This section derives the changed altitude of an inclined string (a ray of light) by refraction during a short time ∆t . We have to consider two different cases, where the string heads downward and upward.

Then, we take into account all possible directions.

Let T(r) be the time ratio between the time at a distance r and the time at infinity. The distance r is the coordinate distance from the center of gravitation. The relationship between the elapsed time at a distance r, ∆t(r), and the elapsed time at infinity, ∆t(∞), is given by

Let T_r(r⁰) be the relative time at the distance r⁰ from the viewpoint of an object that is at the distance r, then T_r(r⁰) is defined by

The relative time at the distance r + ∆r from the viewpoint of the object that is at the distance r, T_r(r + ∆r), is

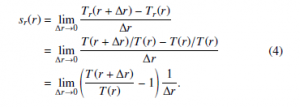
The amount of refraction depends on the relative time (see Eq. (10)). (Postulate 2) Hence, we assume that the slope of the relative time s_r(r) determine the gravitational acceleration and follow the divergence theorem. This means that s_r(r) is proportional to the mass of the gravitational source and the inverse square of coordinate distance, as in the following equation.

This equation is used to find the gravitational acceleration in the next section.

3.1.1     Downward

This section derives the vertical acceleration for a string with an inclined angle.

∆r is the small change in vertical distance that a string flows during a small time ∆t.

In Figure 2, time is slower in the lower space than in the upper space that is illustrated with a brighter rectangle. We have to be aware of that the time dilation across spaces is continuous even though Figure 2 makes it appear to be discontinuous.

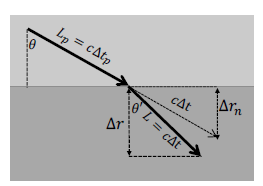
Figure 2: Refraction when an inclined string travels downward.

Accordingly, it takes ∆t in the lower space while it takes ∆t_p in the upper space. The former is less than the latter (∆t < ∆t_p). The length that a string travels is L in the lower space while it is L_p in the upper space during the same coordinate time. L is c∆t and L_p is c∆t_p, where c is the speed of light in vacuum. The difference in the distances traveled in the different spaces causes refraction.

When an inclined string makes an incident angle θ with the vertical line, the incident angle changes into θ⁰ after a short time ∆t. The refraction index n describes the relationship between the incident angle θ and the refraction angle θ⁰ is given by Snell’s law

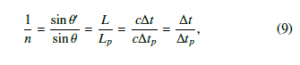
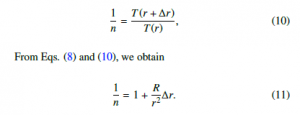
where sinθ is substituted with s to simplify the equation. Using the quadratic formula, the change in vertical distance, ∆r, is given by

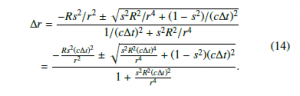
Let ∆r_d be the change in vertical distance when a string heads downward; then it is always negative. Hence, ∆r_d is chosen as the negative version of the two solutions of Eq. (14).

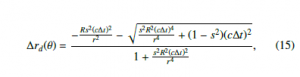
where s = sinθ and 0 ≤ θ < π/2.

When a string is parallel to the horizontal plane (θ = π/2), there might be no gravitational acceleration. Hence, π/2 is excluded in Eq. (15). This special case is discussed in Section 5.

Let ∆r_n(θ) be the vertical distance traveled if it is not affected by refraction, as shown in Figure 2. Then the small change of the downward velocity is given by

where 0 ≤ θ < π/2.

The gravitational acceleration is determined by the incident angle θ of the string. Acceleration is minimized when the incident angle is perpendicular to the horizontal plane of the gravitation. However, Newtonian gravitation is statistically composed of various incident angles. This is described in the Section ’Every Direction’.

3.1.2     Upward

Here, let’s consider a case where a string flows upward, as shown in Figure 3. The incident angle of a string, θ, is greater than π/2 and less than π. let φ = π − θ. We get the same equation as for the refraction index, Eq. (9).

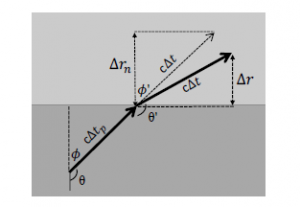
Figure 3: a refraction when an inclined string travels upward.

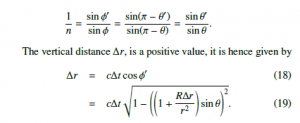
It has a different sign than Eq. (12). However, this equation (19) results in the same quadratic equation as Eq. (13).

Let ∆r_u be the change in distance when a string heads upward. ∆r_u is chosen as the positive version of the two solutions of Eq.

where s = sinθ and π/2 < θ ≤ π.

3.1.3      Every Direction

If we remember the first postulate, the strings comprising a particle flow in several directions depending on its geometry with the speed of light inside its particle space. Multiple particles that are combined with each other make statistically omnidirectional flows, which is regulated by Newtonian gravitation. Hence, we consider all incident angles.

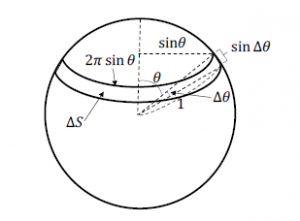
Figure 4: Each incident angle has different amount of area in the three-dimensional space.

The flow directions are evenly distributed in a sphere. Each different incident angle makes a different ring area ∆S in the sphere as shown in Figure 4. The number of flows with the incident angle θ is proportional to the ring area ∆S(θ), which is given by

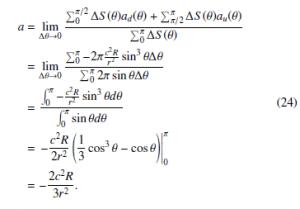
3.2        Newtonian Gravitation

All particles consist of strings and participate in creating gravitation and respond to gravitation. An object that moves with high-speed experiences both time dilation and Lorentz contraction according to the Lorentz transformations. The string flows at the speed of light. Hence, we can expect not only gravitational time dilation but also gravitational spatial contraction around strings. Gravitational spatial contraction corresponds to the curved space of general relativity.

The acceleration created by gravitational spatial contraction is the same as that produced by gravitational time dilation. So, the total refractional acceleration created by both time and space is doubled from Eq. (17) and described by the formula

3.3        Gravitational Time Dilation Function

3.3.1    Proposed function

This section shows a derivation of this gravitational time dilation function T(r).

We go back to Eq. (1). The gravitational time dilation function T(r) is used to obtain a locally measured (proper) time dτ from the coordinate time dt, which is the time measured by a stationary clock at infinity.

3.3.2     Prior work

Here, we compare the proposed solution with the prior solution of general relativity. The Schwarzschild metric as a solution to the

Einstein field equations is

This potential energy is for a flat spacetime where dl can be replaced by dr. l is the locally measured (proper) length. r is the coordinate length measured at infinity.

Here, this paper proposes a new potential energy for a curved spacetime. The gravitational potential energy at a local position l is

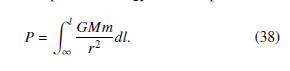
We can get the the classical equation (37), if dl are replaced by dr in Eq. (38). However, the energy is the product of the force and the length that is locally measured at the viewpoint of the object. The local displacement dl is longer than the coordinate displacement dr in a curved spacetime. Hence, we should not use dl instead of dr, and the classical potential energy cannot be used in a curved spacetime.

3.3.3     Comparison with the prior work

If R/r  1 (sluggish spacetime), the proposed equation T(r) has a form similar to the Schwarzschild metric. The Taylor series of the proposed time dilation function can be written

where it is valid for a sluggish spacetime.

Eq. (41) has a form similar to Eq. (36), but Eq. (41) has 3/2 instead of 2 in Eq. (36). The reason for this difference is that the straight string (photon) has different gravitational acceleration than composite bodies with multi-directional flows, but the general relativity assumes that the straight string and composite bodies are equivalent.

3.4        Gravitational Spatial Contraction

Let S(r) be the gravitational spatial contraction function. S(r) determines how much space at the coordinate distance r is contracted. Spatial contraction is reciprocal to time dilation according to the Lorentz transformation. So, the spatial contraction function is

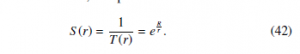
Let l be the locally measured (proper) length. Let r be the coordinate length measured at infinity. The relationship between the two lengths can be expressed by

The Schwarzschild metric includes the counterpart of the spatial contraction function as the following equation:

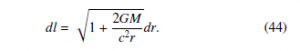
Eqs. (43) and (44) are different for the reason explained in the previous section.

Figure 5 compares the two equations. Eq. (43) can produces a much greater space for blackholes than Eq. (44). This may give us a new clue for dark matter.

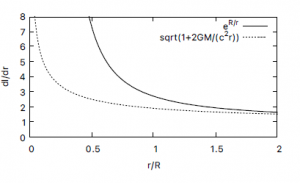
Figure 5: Comparison of the space ratio (dl/dr) using the proposed metric (e^R/r) and general relativity (^p1 + 2GM/(c²r)).

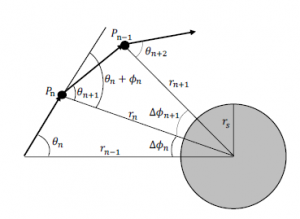
Figure 6: The trajectory of light bended by a star.

4. Gravitational Lens

When a ray of light travels around a star, we can determine the light trajectory if the incident angle, the distance from the star, and the mass of the star are given.

4.1        Numerical Method

This section describes a numerical method that finds the light trajectory around a star. It is useful even if R/r is not small. The next section introduces an analytical method that is valid when R/r  1.

As shown in Figure 6, the stellar radius is r_s. The given distance from the center of the star is r_n. The given incident angle of light is θ_n. The next distance from the star, r_n+1, after a short time ∆t, is

For the short time ∆t, the angle made by the previous position, the center of the star, and the next position of light, ∆φ_n, is obtained by

The refraction index is obtained from the time ratio (Eq. (9)) and the space ratio because the total refraction is caused by both space and time.

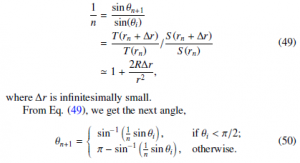
We can iterate the sequences of Eqs. (45) to (50) to get the light trajectory using a computer program.

4.2        Analytical Method

4.2.1     The prior method

The amount of light-bending seen from the Earth can be obtained by a geodesic in a curved spacetime which is introduced in general relativity. In 1911, Einstein obtained a deflection angle of

where r is the visual distance in solar radii from the center of the Sun.

In 1915, he modified the above equation by adding the effect of curved space thus doubling the bending angle in the following equation:

The derivation of this equation is described in prior articles [20].

This derivation is obtained from the velocity of light in a gravitational field. Using Eqs. (36) and (44), we obtain the velocity of light

where GM/(c²r)  1.

The full derivation of light-bending is too long to contain in this paper.

4.2.2    Proposed method

From Eqs. (28), (34), and (43), our counterpart of Eq. (53) can be written as

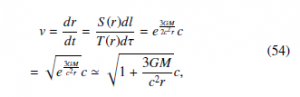
where GM/(c²r)  1.

To get the angle of light-bending using the proposed method, we can substitute Eq. (53) with Eq. (54). Finally, the angle of light-bending is obtained by substituting 4 of Eq. (52) with 3.

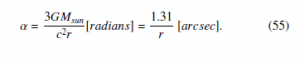
4.3        The Expeditions: Gravitational Refraction and Solar Atmospheric Refraction

Over the last century, there have been many expeditions to measure light-bending during a total eclipse. Goldoni and Stefanini summarized these observational results [21].

In 1919, two expeditions obtained the values 1.61 ± 0.30 and 1.98 ± 0.16 arcsec, where 1/r is omitted. In 1922, the obtained mean values ranged from 1.42 arcsec to 2.16 arcsec. Freunclich et al. obtained an average value of 2.24 ± 0.1 arcsec in 1929. Japanese astronomers gave the average deflection value of 1.71 arcsec in 1936, but their plates were quite unreliable. Subsequent expeditions obtained 2.01 ± 0.27, 1.70 ± 0.10, 1.66 ± 0.18, and 1.75 ± 0.06 arcsec, in 1947, 1952, 1973, and 2017, respectively. Even in the latest result, the most critical item is that the plate scale is only 2 arcsec per pixel [22]. This low resolution makes it hard to obtain an accurate result.

The major factors that can bend light are the atmospheric refraction of the Earth, the solar gravitational refraction (deflection), and the solar atmospheric refraction. Prior measurements considered the atmospheric refraction of the Earth but excluded that of the Sun.

NASA revealed that the solar atmosphere, called the corona, is much larger than previously observed [23]. Its radius is 12 solar radii, and the solar atmosphere is sparsely filled with solar particles, which can slow down the speed of light and causes solar atmospheric refraction. The past observations for light bending are measured within the solar atmosphere.

The particle density in the solar atmosphere can also vary. This may be one of the reasons why the observational results were various. Unfortunately, we don’t have enough information to know how much the solar atmosphere can refract light.

Due to the solar atmospheric refraction, observations should be greater than the proposed expectation of 1.31. Past measurements have ranged from 1.42 to 2.24, which are consistent with the proposed theory.

5. Quantum Gravity

The small change in vertical distance with the incident angle of π/2, ∆r_u(π/2), is zero in Eq. (20). This means that there is no gravitational force to circular strings that are parallel to the horizontal plane of gravitation. The gravitational acceleration for the incident angle of π/2, a_u(π/2), is nonzero in Eq. (22). However, if ∆t is finite like the Planck time. the quantum gravitational acceleration with the parallel angle is obtained as zero from Eq. (21) according to the following equation. ∆v_u(π/2)= 0.

In other words, the gravitational acceleration with the incident angle of π/2 is zero, because the smallest length and the smallest time are finite according to the quantum mechanics.

A lonely and stationary string with a circular shape can rotate like a gyroscope, maintaining its rotational axis perpendicular to the gravitational horizontal plane. When its incident angle become π/2 by gyroscopic rotation, there is no gravitational force to this string. This explains how neutrinos have elusive mass [24] and how the gluon acts like being massless.

A massive particle and a set of combined particles may create nearly omnidirectional flows, which would regulate them to Newtonian gravitation. However, a free, stable, and lonely particle can also have imperfect omnidirectional flows, which will result in a preferred orientation, to minimize gravitational force.

The gravitation is created by the strings. The strings interact with the gravitation. Therefore, the gravitation in the microscopic world depends on quantum mechanical geometric shapes of the strings. This proposed theory is an entirely alternate theory of quantum gravity. However, this may provide a clue for quantum gravity [25, 26], supergravity [27, 28], and loop quantum gravity [29, 30, 31].

Quantum gravity describes gravity according to quantum mechanics. Supergravity assumes the graviton has a superpartner. Quantum gravity and supergravity postulate that the graviton is a messenger particle of gravity. In these theories, the photon and the gluon as force carriers for the electromagnetic interaction and the strong interaction are massless. According to the proposed theory, without the postulate of graviton, we can explain the gravitation is created by all kinds of particles and some particles act like being massless.

Loop quantum gravity (LQG) is a theory that merges quantum mechanics and general relativity. LQG postulates that the structure of space is composed of loops woven into an extremely fine network with a scale on the order of a Planck length. Particles consist of certain patterns of braiding of open and closed strings [13], which can be modeled as the loop network. According to the proposed theory, the source of gravitation is the strings, so the gravitation can be modeled with quantum loops of open and closed strings.

The Compton Scattering experiment shows that photons have momentum [32]. The several studies proposed and measured that the photon consists of a positive charge and a negative charge [33, 34]. The photon is made out of the electromagnetic wave. This means that the electromagnetic wave can create momentum and charges. In addition, it can create gravitation and respond to gravitation.

6. Summary

This paper includes a complete derivation of the equation of Newtonian gravitation from gravitational time dilation using the refraction principle. All particles participate in creating gravitation and respond to gravitation.

The gravitational acceleration depends on the incident angle, which explains why Newtonian gravitation is not regulated at the level of particles. However, a set of multiple restrained particles will result in nearly omnidirectional flows and can be regulated to Newtonian gravitation.

Gravitation is caused by not only curved space but also curved time. Composite bodies have less gravitational acceleration than a photon with an incident angle of π/2 by 2/3.

The gravitational time dilation is an inverse exponential function, whose exponent is proportional to the mass and the inverse of separation from the gravitational source. This is different than the Schwarzschild metric, but it has a form similar to that in a sluggish spacetime because the general relativity mistakenly uses a part of classical physics (potential energy) which is suitable for a flat spacetime.

Acknowledgment

This work was conducted while a Sabbatical at Jungwon University in 2020.

Conflict of Interest

The author declares no conflict of interest.

1. J. B. Hartle, Gravity: An introduction to Einstein’s general relativity, American Association of Physics Teachers, 2003, doi:10.1119/1.1604390.
2. C. M. Will, Theory and experiment in gravitational physics, Cambridge univer- sity press, 2018.
3. R. V. Pound, G. A. Rebka Jr, “Gravitational red-shift in nuclear resonance,” Physical Review Letters, 3(9), 439, 1959, doi:10.1103/PhysRevLett.3.439.
4. R. V. Pound, J. L. Snider, “Effect of gravity on gamma radiation,” Physical Review, 140(3B), B788, 1965, doi:10.1103/PhysRev.140.B788.
5. C. Brans, R. H. Dicke, “Mach’s principle and a relativistic theory of gravitation,” Physical review, 124(3), 925, 1961, doi:10.1103/PhysRev.124.925.
6. M. Gasperini, “Singularity prevention and broken Lorentz symmetry,” Classical and Quantum Gravity, 4(2), 485, 1987, doi:10.1088/0264-9381/4/2/026.
7. J. D. Bekenstein, “Relativistic gravitation theory for the modified Newto- nian dynamics paradigm,” Physical Review D, 70(8), 083509, 2004, doi: 10.1103/PhysRevD.70.083509.
8. K. Nordtvedt Jr, “Equivalence principle for massive bodies. I. Phenomenology,” Physical Review, 169(5), 1014, 1968, doi:10.1103/PhysRev.169.1014.
9. C. M. Will, K. Nordtvedt Jr, “Conservation laws and preferred frames in rela- tivistic gravity. I. Preferred-frame theories and an extended PPN formalism,” The Astrophysical Journal, 177, 757, 1972.
10. M. Pawłowski, R. Raczka, “A unified conformal model for fundamental in- teractions without dynamical Higgs field,” Foundations of Physics, 24(9), 1305–1327, 1994, doi:10.1007/BF02148570.
11. C. Csaki, C. Grojean, L. Pilo, J. Terning, “Towards a realistic model of Higgs- less electroweak symmetry breaking,” Physical review letters, 92(10), 101802, 2004, doi:10.1103/PhysRevLett.92.101802.
12. C. Csaki, C. Grojean, H. Murayama, L. Pilo, J. Terning, “Gauge theories on an interval: Unitarity without a Higgs boson,” Physical Review D, 69(5), 055006, 2004, doi:10.1103/PhysRevD.69.055006.
13. S. O. Bilson-Thompson, F. Markopoulou, L. Smolin, “Quantum gravity and the standard model,” Classical and Quantum Gravity, 24(16), 3975, 2007, doi:10.1088/0264-9381/24/16/002.
14. X. Calmeta, N. Deshpandeb, X. Hec, S. Hsub, “Invisible Higgs boson, contin- uous mass fields and unHiggs mechanism,” arXiv preprint arXiv:0810.2155, 2008, doi:10.1103/PhysRevD.79.055021.
15. M. Carena, H. E. Haber, “Higgs boson theory and phenomenology,” Progress in Particle and Nuclear Physics, 50(1), 63–152, 2003, doi:10.1016/ S0146-6410(02)00177-1.
16. M. Born, E. Wolf, Principles of optics: electromagnetic theory of propagation, interference and diffraction of light, Elsevier, 2013.
17. R. Gupta, A. Pradhan, S. Gupta, “Refraction-Based Alternative Explanation for: Bending of Light Near a Star, Gravitational Red/Blue Shift and Black-Hole,” arXiv preprint arXiv:1004.1467, 2010.
18. X.-H. Ye, Q. Lin, “Gravitational lensing analysed by the graded refractive index of a vacuum,” Journal of Optics A: Pure and Applied Optics, 10(7), 075001, 2008, doi:10.1088/1464-4258/10/7/075001.
19. P. S. Wesson, Five-dimensional physics: classical and quantum consequences of Kaluza-Klein cosmology, World Scientific, 2006.
20. T. Yarman, A. Kholmetskii, M. Arik, “Bending of light caused by grav- itation: the same result via totally different philosophies,” arXiv preprint arXiv:1401.3110, 2014.
21. E. Goldoni, L. Stefanini, “A century of light-bending measurements: bringing solar eclipses into the classroom,” Physics Education, 55(4), 045009, 2020, doi:10.1088/1361-6552/ab8778.
22. D. G. Bruns, “Gravitational starlight deflection measurements during the 21 Au- gust 2017 total solar eclipse,” Classical and Quantum Gravity, 35(7), 075009, 2018, doi:10.1088/1361-6382/aaaf2a.
23. K. C. Fox, “NASA’s STEREO Maps Much Larger Solar Atmosphere Than Pre- viously Observed,” https://www.nasa.gov/content/goddard/nasas-stereo-maps- much-larger-solar-atmosphere-than- previously-observed/, June 25, 2014.
24. M. Aker, K. Altenmu¨ller, M. Arenz, M. Babutzka, J. Barrett, S. Bauer, M. Beck, Beglarian, J. Behrens, T. Bergmann, et al., “Improved upper limit on the neutrino mass from a direct kinematic method by KATRIN,” Physical review letters, 123(22), 221802, 2019, doi:10.1103/PhysRevLett.123.221802.
25. P. K. Townsend, “Four lectures on M-theory,” arXiv preprint hep-th/9612121, 1996.
26. M. J. Duff, “M theory (The Theory formerly known as strings),” Interna- tional Journal of Modern Physics A, 11(32), 5623–5641, 1996, doi:10.1142/ S0217751X96002583.
27. C. V. Johnson, “Jackiw-Teitelboim supergravity, minimal strings, and matrix models,” Physical Review D, 103(4), 046012, 2021, doi:10.1103/PhysRevD. 103.046012.
28. D. Stanford, E. Witten, “JT gravity and the ensembles of random matrix theory,” arXiv preprint arXiv:1907.03363, 2019.
29. P. A. M. Casares, “A review on Loop Quantum Gravity,” arXiv preprint arXiv:1808.01252, 2018.
30. T. Thiemann, “Loop quantum gravity: an inside view,” in Approaches to funda- mental physics, 185–263, Springer, 2007, doi:10.1007/978-3-540-71117-9 10.
31. C. Rovelli, “Loop Quantum Gravity Living Reviews in relativity http://www.livingreviews.org/Articles,” Volume1/1998-1rovelli, 1998.
32. A. H. Compton, “A quantum theory of the scattering of X-rays by light ele- ments,” Physical review, 21(5), 483, 1923, doi:10.1103/PhysRev.21.483.
33. A. Hankins, C. Rackson, W. Kim, “Photon charge experiment,” American Journal of Physics, 81(6), 436–441, 2013, doi:10.1119/1.4793593.
34. H. W. Giertz, “The photon consists of a positive and a negative charge, measuring gravity waves reveals the nature of photons,” 2013.

(Click Here)