1. Introduction

A significant development of chaos occurred after the publication by Lorenz [1] of a work related with the existence of non-periodic solutions in a model formed by nonlinear differential equations. Lorenz’s contribution provided the interest in studying deterministic systems that generate dynamic trajectories strongly influenced by sensitivity to initial conditions. However, it was until 1975 when the term chaos was introduced [2], since then chaotic systems have been studied intensively, and this is one important area of current research in physics, mathematics, and engineering. The analysis of nonlinear complex dynamic behaviors has led to important technological application. In particular the analysis of chaotic oscillators has had important advances in process engineering, cryptography of images, secure data transmission, life science, and information processing, between others [3]–[5].

There are several definitions about chaotic systems. However, in general terms, a chaotic system is a deterministic dynamic system that exhibits irregular behavior, similar to random behavior [6, 7]. A very important aspect in relation to chaos theory is the synchronization of chaotic systems. Since Pecora and Carrol [8] showed that two seemingly random and unpredictable chaotic behaviors can converge in a single trajectory, new expectations arose around chaos theory, trying to solve its control, understanding and prediction.

The synchronization of chaotic systems consists of coupling two or more chaotic systems, after a transitory time, they exhibit identical chaotic oscillations. Synchronization can be solved from the point of view of control theory, designing a slave system which follows the variables of the master system. In the open literature has been presented a lot of important contributions for the design of control schemes for synchronization purposes in chaotic oscillators [9]–[11], observer based controllers [12, 13], adaptive algorithms [14, 15], optimal controllers [16, 17] and so on [18]–[20].

From the above, control theory has been looking for advanced techniques in order to reach a high performance in the operation of processes, in particular with dynamic systems with complex behavior, such as the nonlinear fractional-order systems [21]–[23]. The fractional calculus for the study of dynamic systems with chaotic behavior has emerged as an alternative framework, since it has been proved that it is possible that a class of systems exhibits chaos despite its order is fractional [24]–[27]. Generally, nonlinear systems display complex dynamic behavior as steady state multiplicity, instabilities, complex oscillations and so on under different initial conditions, external disturbances and time-varying parameters, leading to chaotic dynamic behaviors. However, besides of the scientific interest on the study and analysis of nonlinear system with exotic dynamic behaviors, the applications for engineering purposes have been growing importantly [28]–[31].

There are many engineering applications based on dynamical systems with fractional operators, for instance: fractional modelling of the human arm dynamics [32], modelling and identification of viscoelastic mechanical systems [33], modelling of electrical systems [34], analysis and control of economics and financial systems [35, 36], vibration and acoustics phenomena [37], modeling of friction in electric machines [38], problems in electrochemistry, biophysics and bioengineering [39]–[41], methods for signal and image processing [42, 43], applications in automatic control, mechatronics and robotics [44]–[46], among others [47]–[51]. However, there are a few practical applications in this field to prove the feasibility of the physical realization of the proposed techniques [52]–[54]. Some works deal with the master-slave synchronization of fractional-order systems via unidirectional linear coupling [55]–[58], where the proposed methods are applied in the synchronization of fractional-order Rossler, Chua, Chen, unified systems and so on.¨

The main contribution of this work is to achieve the synchronization of a class of fractional-order systems and its verification via the equivalent electronic circuit by means of a proportional control, a nonlinear fractional-order proportional-integral control and an active control. The synchronization implies that all trajectories of the slave system tend to follow all trajectories of the master system. In this sense, the main problem is to find a control input such that the synchronization is possible. The suitable conditions for the synchronization are obtained by solving the dynamical equation of the synchronization error. Furthermore, to verify the effectiveness of the suggested approach we have implemented an electronic circuit using Matlab-Simulink’s Simscape library to obtain the synchronization regime between two fractional-order unified chaotic systems for the same order.

2. Fractional-order feedback controllers

The master system of fractional order α can be represented by,

with x_i(0) = x_i0, i = 1,2,…,n, x = [x₁, x₂, …, x_n]^T ∈ Ω ⊂ Rⁿ is the state vector, and f : Ω → Rⁿ is a nonlinear continuous function.

In (1), the fractional derivative of x_i is defined as [? ],

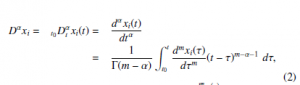
where: α ∈ R⁺, m − 1 ≤ α < m, m ∈ N, _dτm is the m-th time derivative of x_i and Γ is the gamma function.

2.1     Proportional control

Let us propose the controlled slave system of fractional order α as follows,

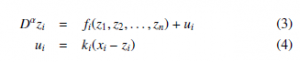
with z_i(0) = z_i0, i = 1,2,…,n, z = [z₁, z₂, …, z_n]^T ∈ Ω ⊂ Rⁿ is the state vector of the slave system, and k_i is the proportional gain. Let us define the synchronization error as,

The synchronization performance is obtained by means of the analysis of the dynamics of the synchronization error.

First, we take the time derivative of order α of (5),

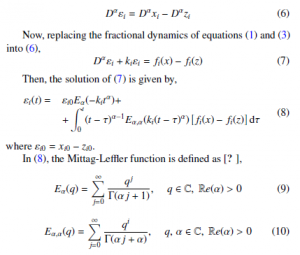
To guarantee the convergence of the synchronization error in (8),

Assumption 1 and 2 are introduced,

Assumption 1 | f_i(x) − f_i(z)| ≤ L_i < ∞

Assumption 2 The proportional gain is positive.

Applying Assumption 1 in (8) we have,

From the previous analysis, the following proposition is established.

Proposition 1 If Assumptions 1 and 2 are fulfilled, then the synchronization of the master system (1) and the controlled slave system (3)-(4) is achieved, where, the trajectories of ε_i belongs to a closed ball with radius proportional to L_i/k_i.

2.2     Nonlinear fractional-order PI control

Let us consider (1) as the master system. In this case, the slave system is described by,

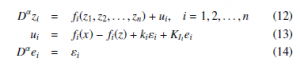
where, ε_i = x_i − z_i, k_i is the proportional gain and K_Ii is the integral gain.

Property 1 (see [59]) Let I^α be the fractional integral of order α.

Then,

For 0 < α < 1, the interconnected system (17)-(19) is asymptotically stable if,

Hence, (21) is asymptotically stable if |arg(eig(P))| > .

2.3    Active control

Let us represent the master system (1) as,

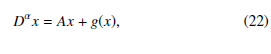
In (22), g : Ω → Rⁿ is a nonlinear continuous function and the matrix A ∈ R^n×n is defined by,

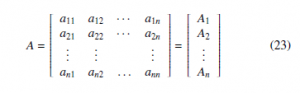
h i where, a_ij are constant coefficients and A_i = a_i1                 a_i2                 · · ·           a_in denotes the i-th row of matrix A, for i = 1,2,…,n.

Then, master system (22) can be rewritten as,

3. The fractional-order unified chaotic system

Consider the fractional-order master system [54],

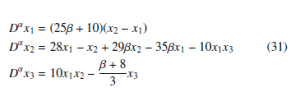
With β = 1 and α = 0.9 system (31) exhibits chaotic behavior, in the sense of Definition 1.

Definition 1 ([6]) An attractor is said to be chaotic if it is bounded and all the trajectories starting form it are Lyapunov unstable. Then, a dynamic system is chaotic if it has at least one chaotic attractor.

System (31) is simulated through the Matlab-Simulink diagram shown in Figure 1, where blocks F1, F2 and F3 correspond to the approximation of the integral operator with order α = 0.9.

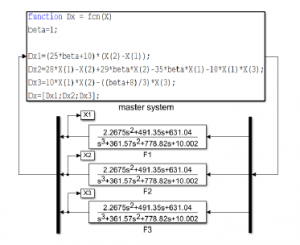
Figure 1: Simulation of system (31) using Matlab-Simulink

For simulation purposes, initial condition of block F1, was set to -0.001. Figure 2 shows the numerical simulation of system (31) via the phase portraits.

Now, in order to illustrate the behavior of system (31), we change the weight parameters (α, β). The simulation results are given in Figure 3 with parameters: (a) α = 0.9, β = 0, (b) α = 0.9, β = −1, (c) α = 0.8, β = 0.5 and (d) α = 0.7, β = 1.

Clearly, system (31) is not chaotic with these set of parameters, where the integral operator with orders α = 0.8 and α = 0.7 is defined by [24],

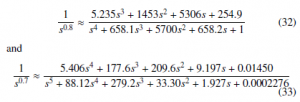
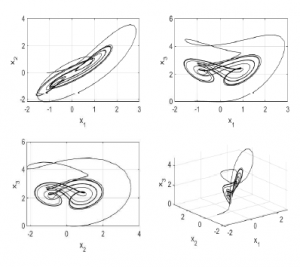
Figure 2: Simulation results of system (31), β = 1 and α = 0.9.

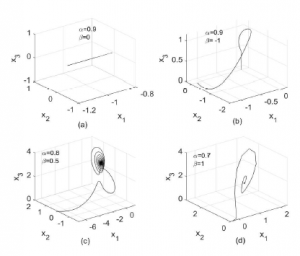
Figure 3: Phase portraits of system (31) with different values of (α,β)..

4. Synchronization results and discussion

The fractional-order slave system that synchronizes with system (31) is represented as,

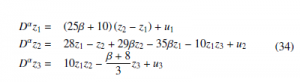
where β = 1, α = 0.9 and u₁, u₂ and u₃ are the control signals.

It is necessary to calculate the control gains values. First, for the proportional control, we obtain the constants L_i over the bounded set Ω = {x ∈ Rⁿ | |x_i| ≤ M_i},

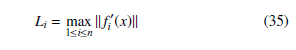
where f_i⁰(x) is the Jacobian matrix.

Then, considering that M₁ ≈ 2, M₂ ≈ 3 and M₃ ≈ 4, we have that L₁ = 35, L₂ = 47, and L₃ = 30.

According to Proposition 1, the maximum synchronization errors are defined as

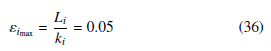
In Equation (36) we consider the synchronization errors are bounded by 0.05, they are acceptable for complete practical synchronization. Equation (36) yields to k₁ = 700, k₂ = 940, and k₃ = 600.

For the nonlinear PI controller, the gain values are obtained in order to guarantee a settling time of 0.02s and an overshoot of 1% in the three coordinates, then ki = 400 and K_Ii = 58613, for i = 1,2,3. And for the active controller we have the following conditions,

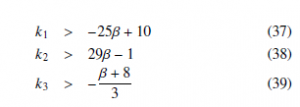
In this case, we choose k₁ = 200, k₂ = 100 and k3 = 100.

Figure 4 shows the phase portraits of the master and slave systems when the control signals are off, clearly all systems are unsynchronized due to the initial conditions are different. However, when the feedback controllers are activated the synchronization is achieved since the trajectories of the controlled slave system tend to follow the trajectories of the master system.

In Figure 5 the synchronization performance is verified via the synchronization errors. We observe that the synchronization errors converge to zero when the feedback control is activated. As we can note, the corresponding slave trajectory reach almost immediately the master trajectory for the proportional control, also, when the nonlinear PI control acts, the corresponding trajectory has a higher oscillatory overshoot and a settling time of 0.02s, and for the active control, the synchronization errors converge exponentially to zero at 0.02 s.

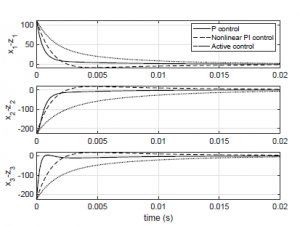
Figure 5: Synchronization errors.

The above-mentioned behaviors for the state variables under feedback controllers can be explained for the performance of the three controllers under comparison. Figure 6 is related to the control effort performance, it can be observed that the control effort for the proportional controller is very high due to the magnitude presented at the startup and transient condition. On the other hand, PI and larger settling time.

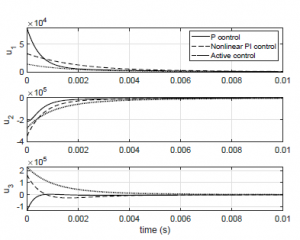
Figure 6: Control signals.

5. Equivalent electronic circuit

introduced in Section 2. In order to obtain −z₁, −z₂ and −z₃, in this circuit, for each signal z₁, z₂ and z₃ is added an inverting operational System (31) is translated to the electric circuit shown in Figure 7. amplifier with unity gain, the value of R is equal to 10kΩ. To avoid the crossing of physical lines we employ connection labels. The label block makes connections between two blocks without using Fractional integrators blocks F1, F2 and F3 are represented as Figure 8 shows the approximation of  as an electric circuit  pled since the control inputs require information signals from both using the Simscape libraries. circuits.

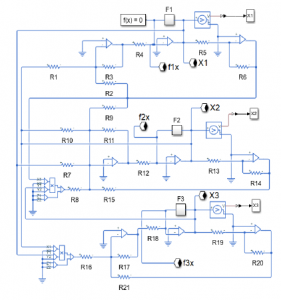
Figure 7: Electrical model of master system (31) using Simulink’s Simscape library.

The equivalent circuit for the proportional control (4) is shown in Figure 10. Resistors R_P1, R_P2 and R_P3 are related with the control gains of Section 4 as follows,

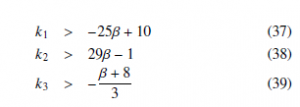
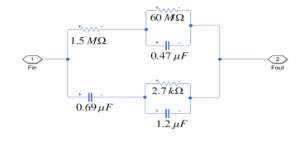
Figure 8: Integrator blocks F1, F2,…, F12.

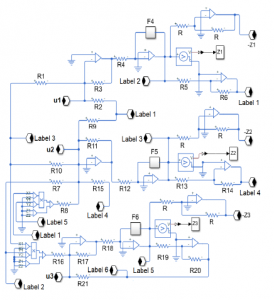
Figure 9: Electrical circuit schematic for the slave system (34).

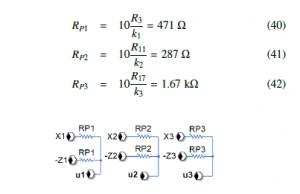
Figure 10: Proportional control.

6. Verification of the master-slave synchronization

The synchronization is verified via the equivalent electronic circuits of master and slave systems. The controlled slave electronic circuit is given in Figure 9, where u1, u2 and u3 are the control inputs Figure 10: Proportional control.

The nonlinear fractional-order PI control (13)-(14) is proposed by means of the circuit of Figure 11.

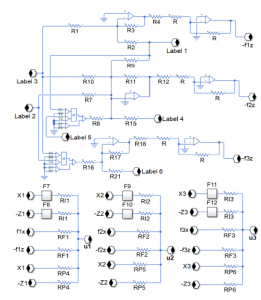
Figure 11: Nonlinear fractional-order PI control.

The parameter values are obtained as,

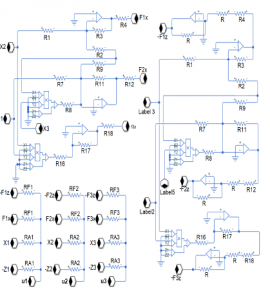
Figure 12: Active control.

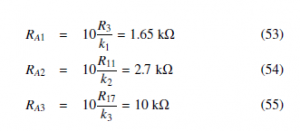
Figure 13 shows the phase portraits of the master-slave synchronization obtained by means of the equivalent electronic circuits given by Figures 7 and 9 along with the control inputs of Figures

10, 11 and 12. For all simulations, initial voltage on capacitor of 0.69µF takes several arbitrary values: 1 V (block F1), -2 V (block F4), 1 V (block F5), 1 V (block F6), while the rest of capacitors remain at 0 V. Notably, the whole phase portrait of the controlled slave system is synchronized with the corresponding phase portrait of the master system using the proposed controllers, for arbitrary initial conditions. However, an important characteristic is that the nonlinear fractional-order PI control and the active control lead to complex circuit structures.

[4]    M. H. Abd, F. R. Tahir, G. A. Al-Suhail, V. T. Pham, “An adaptive observer synchronization using chaotic time-delay system for secure communication,” Nonlinear Dynamics, 90, 2017, doi:10.1007/s11071-017-3825-2.

[5]    H. Li, X. Liao, M. Luo, “A novel non-equilibrium fractional-order chaotic system and its complete synchronization by circuit implementation,” Nonlinear Dynamics, 68, 2012, doi:10.1007/s11071-011-0210-4.

[6]    A. L. Fradkov, Cybernetical Physics, From Control of Chaos to Quantum Control, 2007.

[7]    R. Femat, G. Solis-Perales, “Robust synchronization of chaotic systems via feedback,” 2008, doi:10.1007/978-3-540-69307-9.

[8]    L. M. Pecora, T. L. Carroll, “Synchronization in chaotic systems,” Physical Review Letters, 64, 1990, doi:10.1103/PhysRevLett.64.821.

[9]    S. Boccaletti, J. Kurths, G. Osipov, D. Valladares, C. Zhou, “The synchronization of chaotic systems,” Physics reports, 366(1-2), 1–101, 2002.

L. Huang, R. Feng, M. Wang, “Synchronization of chaotic systems via nonlinear control,” Physics Letters, Section A: General, Atomic and Solid State

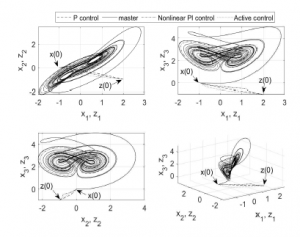
Figure 13: Master-slave synchronization.

7. Conclusions

This work studied the master-slave synchronization in a class of chaotic systems with fractional-order via feedback control. First, the feedback controllers were designed. In this sense, a proportional control was proposed, it guarantees that the synchronization error is bounded, as well as, a nonlinear fractional-order PI control and an active control were introduced, where the stability of the closed-loop system depends on the control gains, here for both controllers the synchronization error is asymptotically stable. Next, as application example, the fractional-order unified chaotic system was considered as master system. In fact, a set of numerical simulations based on the mathematical models of master and slave system showed that the synchronization is fulfilled by means of the proposed feedback controllers. It is important to mention that the proportional control exhibited the higher control effort, which could be a restriction in another class of systems, for instance, in those involving actuators. On other hand, in the transient condition, the active control is slower than the other ones. Finally, the synchronization was verified with success using the equivalent electronic circuits. As can be noticed, the proportional control has a simple circuit structure.

Conflict of interest

The author declares no conflict of interest.

Acknowledgment

This paper was supported by the Secretar´ıa de Investigacion y Posgrado of the Instituto Polit´      ecnico Nacional´ (SIP-IPN) under the research grant SIP20211509.

1. E. N. Lorenz, “Deterministic Nonperiodic Flow,” Journal of the Atmospheric Sciences, 20, 1963, doi:10.1175/1520-0469(1963)020(0130:dnf)2.0.co;2.
2. T.-Y. Li, J. A. Yorke, “Period Three Implies Chaos,” The American Mathematical Monthly, 82, 1975, doi:10.2307/2318254.
3. G. Li, B. Zhang, “A Novel Weak Signal Detection Method via Chaotic Synchronization Using Chua’s Circuit,” IEEE Transactions on Industrial Electronics, 64, 2017, doi:10.1109/TIE.2016.2620103.
4. M. H. Abd, F. R. Tahir, G. A. Al-Suhail, V. T. Pham, “An adaptive observer synchronization using chaotic time-delay system for secure communication,” Nonlinear Dynamics, 90, 2017, doi:10.1007/s11071-017-3825-2.
5. H. Li, X. Liao, M. Luo, “A novel non-equilibrium fractional-order chaotic system and its complete synchronization by circuit implementation,” Nonlinear Dynamics, 68, 2012, doi:10.1007/s11071-011-0210-4.
6. A. L. Fradkov, Cybernetical Physics, From Control of Chaos to Quantum Control, 2007.
7. R. Femat, G. Solis-Perales, “Robust synchronization of chaotic systems via feedback,” 2008, doi:10.1007/978-3-540-69307-9.
8. L. M. Pecora, T. L. Carroll, “Synchronization in chaotic systems,” Physical Review Letters, 64, 1990, doi:10.1103/PhysRevLett.64.821.
9. S. Boccaletti, J. Kurths, G. Osipov, D. Valladares, C. Zhou, “The synchronization of chaotic systems,” Physics reports, 366(1-2), 1–101, 2002.
10. L. Huang, R. Feng, M. Wang, “Synchronization of chaotic systems via non-linear control,” Physics Letters, Section A: General, Atomic and Solid State Physics, 320, 2004, doi:10.1016/j.physleta.2003.11.027.
11. L. M. Pecora, T. L. Carroll, “Synchronization of chaotic systems,” Chaos: An Interdisciplinary Journal of Nonlinear Science, 25(9), 097611, 2015.
12. Y. Zhao, W. Zhang, H. Su, J. Yang, “Observer-Based Synchronization of Chaotic Systems Satisfying Incremental Quadratic Constraints and Its Application in Secure Communication,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, 50(12), 5221–5232, 2020, doi:10.1109/TSMC.2018. 2868482.
13. S. Mohammadpour, T. Binazadeh, “Observer-based synchronization of uncertain chaotic systems subject to input saturation,” Transactions of the Institute of Measurement and Control, 40, 2018, doi:10.1177/0142331217705435.
14. A. Das, F. L. Lewis, “Distributed adaptive control for synchronization of un-known nonlinear networked systems,” Automatica, 46, 2010, doi:10.1016/j. automatica.2010.08.008.
15. S. Wen, Z. Zeng, T. Huang, “Adaptive synchronization of memristor-based Chua’s circuits,” Physics Letters, Section A: General, Atomic and Solid State Physics, 376, 2012, doi:10.1016/j.physleta.2012.08.021.
16. B. Naderi, H. Kheiri, A. Heydari, R. Mahini, “Optimal Synchronization of Complex Chaotic T-Systems and Its Application in Secure Communication,” Journal of Control, Automation and Electrical Systems, 27, 2016, doi: 10.1007/s40313-016-0245-3.
17. W. D. Chang, “PID control for chaotic synchronization using particle swarm optimization,” Chaos, Solitons and Fractals, 39, 2009, doi:10.1016/j.chaos. 2007.01.064.
18. Z. Liu, “Design of nonlinear optimal control for chaotic synchronization of coupled stochastic neural networks via Hamilton–Jacobi–Bellman equation,” Neural Networks, 99, 2018, doi:10.1016/j.neunet.2018.01.003.
19. C. Huang, J. Cao, “Active control strategy for synchronization and anti- synchronization of a fractional chaotic financial system,” Physica A: Statistical Mechanics and its Applications, 473, 2017, doi:10.1016/j.physa.2017.01.009.
20. R. Mart´inez-Guerra, J. L. Mata-Machuca, “Fractional generalized synchronization in a class of nonlinear fractional order systems,” Nonlinear Dynamics, 77(4), 1237–1244, 2014.
21. X. J. Wen, Z. M. Wu, J. G. Lu, “Stability analysis of a class of nonlinear fractional-order systems,” IEEE Transactions on Circuits and Systems II: Express Briefs, 55, 2008, doi:10.1109/TCSII.2008.2002571.
22. Y. Li, Y. Q. Chen, I. Podlubny, “Mittag-Leffler stability of fractional-order nonlinear dynamic systems,” Automatica, 45, 2009, doi:10.1016/j.automatica. 2009.04.003.
23. S. Liu, W. Jiang, X. Li, X. F. Zhou, “Lyapunov stability analysis of fractional nonlinear systems,” Applied Mathematics Letters, 51, 2016, doi: 10.1016/j.aml.2015.06.018.
24. T. T. Hartley, C. F. Lorenzo, H. K. Qammer, “Chaos in a Fractional Order Chua’s System,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 42, 1995, doi:10.1109/81.404062.
25. C. Li, G. Peng, “Chaos in Chen’s system with a fractional order,” Chaos, Solitons and Fractals, 22, 2004, doi:10.1016/j.chaos.2004.02.013.
26. V. Daftardar-Gejji, S. Bhalekar, “Chaos in fractional ordered Liu system,” Computers and Mathematics with Applications, 59, 2010, doi:10.1016/j.camwa. 2009.07.003.
27. Z. Wang, X. Huang, G. Shi, “Analysis of nonlinear dynamics and chaos in a fractional-order financial system with time delay,” Computers and Mathematics with Applications, 62, 2011, doi:10.1016/j.camwa.2011.04.057.
28. H. G. Sun, Y. Zhang, D. Baleanu, W. Chen, Y. Q. Chen, “A new collection of real-world applications of fractional calculus in science and engineering,” Communications in Nonlinear Science and Numerical Simulation, 64, 2018, doi:10.1016/j.cnsns.2018.04.019.
29. J. A. T. MacHado, M. F. Silva, R. S. Barbosa, I. S. Jesus, C. M. Reis, M. G. Mar- cos, A. F. Galhano, “Some applications of fractional calculus in engineering,” Mathematical Problems in Engineering, 2010, 2010, doi:10.1155/2010/639801.
30. J. Zarei, M. Tabatabaei, “Fractional-order unknown input filter design for fault detection of discrete fractional-order linear systems,” Transactions of the Institute of Measurement and Control, 40, 2018, doi:10.1177/0142331217746493.
31. G. C. Wu, Z. G. Deng, D. Baleanu, D. Q. Zeng, “New variable-order fractional chaotic systems for fast image encryption,” Chaos, 29, 2019, doi: 10.1063/1.5096645.
32. I. Tejado, D. Vale´rio, P. Pires, J. Martins, “Fractional order human arm dynamics with variability analyses,” Mechatronics, 23, 2013, doi:10.1016/j. mechatronics.2013.05.003.
33. J. J. D. Esp´indola, J. M. D. S. Neto, E. M. Lopes, “A generalised fractional derivative approach to viscoelastic material properties measurement,” volume 164, 2005, doi:10.1016/j.amc.2004.06.099.
34. J. Sabatier, O. P. Agrawal, J. A. T. Machado, Advances in fractional calculus: Theoretical developments and applications in physics and engineering, 2007, doi:10.1007/978-1-4020-6042-7.
35. W.-C. Chen, “Nonlinear dynamics and chaos in a fractional-order financial system,” Chaos, Solitons and Fractals, 36(5), 1305–1314, 2008, doi: https://doi.org/10.1016/j.chaos.2006.07.051.
36. S. Dadras, H. R. Momeni, “Control of a fractional-order economical system via sliding mode,” Physica A: Statistical Mechanics and its Applications, 389, 2010, doi:10.1016/j.physa.2010.02.025.
37. D. Klatt, R. L. Magin, F. Mainardi, T. J. Royston, N. C. Perkins, I. Y. Shen, “Special section: Fractional calculus in vibration and acoustics,” 2014, doi: 10.1115/1.4027482.
38. R. Cipin, C. Ondrusek, R. Huzl´ik, “Fractional-order model of DC motor,” 2014, doi:10.1007/978-3-319-02294-9 46.
39. R. L. Magin, “Fractional calculus in bioengineering,” 2004, doi:10.1615/ CritRevBiomedEng.v32.10.
40. K. B. Oldham, “Fractional differential equations in electrochemistry,” Advances in Engineering Software, 41, 2010, doi:10.1016/j.advengsoft.2008.12.012.
41. R. L. Magin, “Fractional calculus models of complex dynamics in biological tissues,” Computers and Mathematics with Applications, 59, 2010, doi: 10.1016/j.camwa.2009.08.039.
42. P. Ghamisi, M. S. Couceiro, J. A. Benediktsson, N. M. Ferreira, “An efficient method for segmentation of images based on fractional calculus and natural selection,” Expert Systems with Applications, 39, 2012, doi: 10.1016/j.eswa.2012.04.078.
43. H. Sheng, Y. Chen, T. Qiu, Fractional processes and fractional-order signal processing: techniques and applications, Springer Science & Business Media, 2011.
44. S. Ghasemi, A. Tabesh, J. Askari-Marnani, “Application of fractional calculus theory to robust controller design for wind turbine generators,” IEEE Transactions on Energy Conversion, 29, 2014, doi:10.1109/TEC.2014.2321792.
45. R. E. Gutie´rrez-Carvajal, L. F. D. Melo, J. M. Rosa´rio, J. A. MacHado, “Condition-based diagnosis of mechatronic systems using a fractional calculus approach,” International Journal of Systems Science, 47, 2016, doi: 10.1080/00207721.2014.978833.
46. L. B. G. Bozzini, “Fractional-order derivatives and their application to the position control of robots,” International Journal of Mechanics and Control, 39, 2009.
47. C. Li, G. Chen, “Chaos and hyperchaos in the fractional-order Ro¨ ssler equations,” Physica A: Statistical Mechanics and its Applications, 341, 2004, doi: 10.1016/j.physa.2004.04.113.
48. W. H. Deng, C. P. Li, “Chaos synchronization of the fractional Lu¨ system,” Physica A: Statistical Mechanics and its Applications, 353, 2005, doi: 10.1016/j.physa.2005.01.021.
49. C. Li, X. Liao, J. Yu, “Synchronization of fractional-order chaotic systems,” Physical Review E – Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 68, 2003, doi:10.1103/PhysRevE.68.067203.
50. R. Mart´inez-Mart´inez, J. Mata-Machuca, R. Mart´inez-Guerra, J. Leo´n, G. Ferna´ndez-Anaya, “Synchronization of nonlinear fractional-order systems,” Applied Mathematics and Computation, 218, 2011, doi:10.1016/j.amc.2011. 08.075.
51. J. D. Gabano, T. Poinot, “Fractional modelling and identification of thermal systems,” Signal Processing, 91, 2011, doi:10.1016/j.sigpro.2010.02.005.
52. M. F. Tolba, A. M. AbdelAty, N. S. Soliman, L. A. Said, A. H. Madian, A. T. Azar, A. G. Radwan, “FPGA implementation of two fractional-order chaotic systems,” AEU – International Journal of Electronics and Communications, 78, 2017, doi:10.1016/j.aeue.2017.04.028.
53. K. Rajagopal, A. Karthikeyan, A. K. Srinivasan, “FPGA implementation of novel fractional-order chaotic systems with two equilibriums and no equilibrium and its adaptive sliding mode synchronization,” Nonlinear Dynamics, 87, 2017, doi:10.1007/s11071-016-3189-z.
54. X. R. Chen, C. X. Liu, F. Q. Wang, “Circuit realization of the fractional-order unified chaotic system,” Chinese Physics B, 17, 2008, doi:10.1088/1674-1056/ 17/5/022.
55. L. G. Yuan, Q. G. Yang, “Parameter identification and synchronization of fractional-order chaotic systems,” Communications in Nonlinear Science and Numerical Simulation, 17, 2012, doi:10.1016/j.cnsns.2011.04.005.
56. J. G. Lu, “Chaotic dynamics of the fractional-order Lu¨ system and its synchronization,” Physics Letters, Section A: General, Atomic and Solid State Physics, 354, 2006, doi:10.1016/j.physleta.2006.01.068.
57. P. Zhou, “Chaotic synchronization for a class of fractional-order chaotic systems,” Chinese Physics, 16, 2007, doi:10.1088/1009-1963/16/5/016.
58. X. Wu, J. Li, G. Chen, “Chaos in the fractional-order unified system and its synchronization,” Journal of the Franklin Institute, 345, 2008, doi: 10.1016/j.jfranklin.2007.11.003.
59. E. Demirci, N. Ozalp, “A method for solving differential equations of fractional order,” Journal of Computational and Applied Mathematics, 236, 2012, doi:10.1016/j.cam.2012.01.005.

(Click Here)