1. Introduction

This original research paper is an extension of the work initially presented in the Congress International de Innovation y Tendencies en Ingenier´ıa (CONIITI) 2020 [1]. In this version, readers can find a full view of the proposed learning distributed method, which uses concepts from Game Theory (GT) to control complex systems. This paper also presents an evaluation of the method from an evolution- ary perspective of the obtained equations. This work also simulates a modified version of the case study presented in the conference, which includes different communication constraints and attributes of the generators employed in the power grid. Moreover, some additional cases in the context of classic games and maximization problems are introduced to make clearer the incidence of some control parameters in the behavior of agents.

The idea to model and control complex systems has increased over time. In this context, Engineering applications have received special interest due to their affinity with the use of mathematical techniques to prove new models and concepts on applications closer to reality [2]. In recent decades, research has been focused on the study of distributed systems with large-scale control. Numerous models and techniques have been developed to overcome issues such as the expensive computational requirements, the structure of the communication, and the calculation of the data required to com- plete a task in large-scale systems. These issues can be managed by using Multi-Agent Systems (MAS) and concepts from game theory [3]. In this sense, the interactions of agents have been thoroughly studied, as some strategies can help agents maximize their outcomes. For example, [4] establishes relations among games, learning, and optimization in networks. Other studies have focused on games and learning [5] or on algorithms for distributed computation in topologies of dynamic networks [6]. Authors in [7] studied the main applications of power control in the frameworks of distributed and centralized game theory. Regarding smart grid control applica- tions, please refer to [8]. Other research has concentrated on cases with issues in coordination and negotiation that guide the study of the interactions of agents[9]. For further studies on applications of power control using game theory, please refer to [10]. Research on game theory considers three types of games. First, continuous games consider the way an agent can have a pure strategy looking for maximum profit. Second, in matrix games, agents are regarded as individuals and can take only one shot to play simultaneously. Finally, dynamic games suppose that players can learn in some way about the environment, that is, their actions and states. This assumption means agents can learn and correct their behavior based on the outcomes of their actions [11]. Dynamic games must deal with the following challenges: modeling the environment for agents interaction, modeling the agents goals, the prioritization of the agents actions, and the estimation of the amount of information owned by a player [12].

The study of dynamics of agents changing over time is a concept of dynamic games introduced by Evolutionary game theory (EGT) [13]. The concept of the evolutionary stable strategy popularized EGT thanks to the analogy with biology concepts and the compari- son with natural behaviors [14]. Some real-life control applications have employed EGT, whose understanding serves as a basis for the replicator dynamics (RD) approach. The revision protocols describe the way agents choose and modify their strategies, while population games determine the agents’ interactions. The combination of both revision protocols and population games produces the concept of evolutionary game dynamics [14]. This perspective of evolution is often used to model large-scale systems because its mathematical background helps to describe this process with differential equations [13]. Many areas of Engineering have applied EGT, for example, optimization problems, control of communication access, systems of microgrids, etc. [11]. The use of EGT to model engineering prob- lems has revealed the following benefits: ease to relate a game to an engineering problem, where payoff functions can be defined with the objective function and the strategies, and the relationship between the optimization concept and Nash Equilibrium, which is enabled under particular conditions that met the conditions of the first-order optimization of the Karush–Kuhn–Tucker. Last but not least, EGT uses local information to achieve solutions. In this sense, distributed approaches emerge to tackle engineering problems, which is useful when considering the implementation cost of centralized schemes and their complexity [11]. Distributed schemes of population dy- namics have outstanding features over techniques like the method of dual decomposition, which requires a centralized coordinator [15]. This characteristic reduces the associated cost with the structure of communication. Additionally, in comparison with distributed learning algorithms in normal-form-games, there are no failures in distributed population dynamics when all the variables involved in decision-making have limitations[16]. This makes Distributed Pop- ulation Dynamics suitable for solving issues regarding allocation of resources like in a smart city design [17]. For these purposes, the distributed power generation needs to be integrated so that electric

grids be more reliable, robust, efficient, and flexible. Nevertheless, modeling a grid using a distributed approach instead of the classic centralized, is an option to consider due to its realism and flexibil- ity, according to microgrids constraints [18]. In this sense, control operations are considered individually in microgrids, as they make a distinction among the power generation, the secondary frequency, and the economic dispatch [19]. Static optimization concepts are employed to manage the economic dispatch [20] or even methods like the offline direct search [21]. The analysis may be more com- plicated if it includes loads, the generator, and power line losses in the distributed model. Other approaches cannot consider the dy- namic conditions like the economic dispatch time dependence [22]. Some approaches have been developed to face these challenges. For instance, [23] presents a management system for a microgrid with centralized energy and stand-alone mode to study its static behavior. Other research employs a distributed control strategy con- sidering power line signaling for energy storage systems [24]. The employment of the MAS framework in economic problems using a distributed approach was gathered in [25], taking into account the delays in the communication system. Microgrid architectures have also been proposed considering distributed systems like the microgrid hierarchical control [26].

This paper presents an approach to overcome some of the is- sues identified in the literature review. The aim is to show how to develop a control method of learning to study the influence of the exploration concept in MAS, that is, interaction between agents. RD was developed from simple learning models [27], so this re- search seeks to bring the exploration concept into the traditional exploration-less expression of RD, using the Q-learning dynamics. As a result, the combination of these frameworks opens up a path to tackle dynamics in a scenario where the feedback of each agent is determined by the agent itself and by other agents, and where interaction between them is limited. For the analysis, the Boltzmann distribution includes a distributed perspective of the Replicator Dy- namics as a way to regulate the agents’ behavior in a determined scenario. The developed method employs a temperature parameter and the presence of entropy terms, to modify the learning agents’ behavior and link the selection-mutation process from EGT and the exploration-exploitation concept from RL. This attribute complies with the traditional positive condition of EGT techniques (modeling agents’ interaction). Nevertheless, In the control area, the employ- ment of these techniques has to be understood more on the normative side of things. To explain these features, this approach employs theory of RL, EGT, and decision-making to solve some cases in the context of classic games and maximization problems using a novel distributed model of learning. It also uses experimental data to tackle an economic dispatch problem, which is a common problem in smart grids. The results obtained by the proposed approach are contrasted with the classical centralized framework of RD.

The remainder of this paper is organized as follows. Section 2 presents, a short synopsis of game theory and reinforcement learn- ing, as well as the relationship between EGT and Q-learning using the Boltzmann distribution. Section 3 explains a distributed neigh- boring concept used for the Boltzmann control method, considering the behavior of replicator dynamics. Section 4 introduces important concepts from the previous Section, related to evolutionary game theory and reinforcement learning. In Section 5, the employment of the learning method on traditional cases of GT and maximization problems presents the background to analyze the application of the Boltzmann model behavior on a smart grid real-life case. Finally, the main conclusions of the study are summarized in Section 6.

2. Preliminaries

Game theory includes a group of equations and concepts to study the background in decentralized control issues. Most of the time, a game comprises a group of players (agents) with similar population behavior that choose the best way to execute actions. The strategy of a player can decrease rewards after performing a wrong action or increase rewards when the action was correct [28]. The theory of learning is used to understand this behavior. In this sense, the scheme of RL explains the relationship among the environment, signals, states, and actions. In the interaction, at each step, each player gets a notification with the current state of the environment and a reinforcement signal, then, the player chooses a strategy. Each player of the game aims to find the policy that produces the best rewards after recognizing the consequence of its actions, that is, reward or punishment. A structure of estimated value functions is characteristic of traditional RL methods [29]. The total reward that a player can obtain is usually a pair state-action or a state value. This means that the optimal value function is needed to find the policy that correctly fulfills payoffs. The Markov decision process and value iteration algorithm can be employed for this purpose [30] when the scenario is familiar. In other cases, Q-learning can be used as an adaptable method of value iteration where the model of the scenario does not require to be specific. Equation (1) depicts the Q-learning interaction process [31]:

provides variety to the population. On the other hand, selection provides priority to some varieties where every genotype is a pure strategy Q_j(n), where the RD offspring expresses this behavior. The general equation of RD [27] is presented in Equation (2).

where x_i is the portion of a population that plays the i-th strategy. The payoff matrix is written as A and it owns diverse payoff val- ues that each replicator obtains from other agents. The vector of probability x = (x₁, x₂, …, x_J) often defines the population state (x), and evidence the diverse density values of each type of replicator. Consequently, (Ax)_i is the payoff obtained by the i-th player with x state. Then, the average payoff would be written as x Ax. Simi- larly, ^dxi symbolizes the growth rate of the population playing the i-th strategy, which is calculated using the obtained payoff value after playing the i-th strategy and its difference with the average population payoff. [34].

2.1        Relating EGT and Q-Learning

In [35], the frameworks of RD and Q-learning are related in the context of two-player games, where players have different strategies. This relationship is conceivable as players can also be considered Q-learners. For modelling this case, a differential equation is needed for player R (rows) and another one for player C (columns). When A = B^t, the standard RD Equation (2) is employed, where x_i is sub- stituted by r_i or c_i. Thence, A or B, and the change in state (x) for r or c determine the payoff matrix for a specific player. Therefore, (Ax)_i switches to (Ac)_i or (Br)_i and is the reward obtained by the i-th player with a r or c state. Likewise, for players R and C, the growth rate ^dxi switches to ^dri or ^dci , respectively. This behavior is

explained using the following system of differential equations [27] with an initial pair of Q_t(s^j, a^j), where (s^j, a^j) represents the newest values of s and a, respectively. max_aj obtains the uppermost value of Q from s^j by selecting the action that increases its value. α represents the general

step size parameter, Γ is the instant reinforcement, and γ is a de- duction parameter. When players have complete access to the game information and there are no communication limitations, the theory of learning and games are valuable instruments to deal with control applications that use a centralized approach. Nevertheless, these models aim to provide a close description of optimal circumstances, but they have some drawbacks when dealing with more realistic conditions, communication constraints, and the individuals ratio-

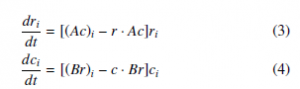
Equations (3) and (4) denote the group of replicator dynamics equations used to model the behavior of two populations. Each population has a growth rate determined by the other populations. For example, A and B denote two payoff matrices that are needed to estimate the rate of change for two different current players in the problem using this group of differential equations. To find the rela- tionship between the Q-learning framework and the RD equations, Equation (5) is introduced:In this vein, EGT tries to loosen the idea of rationality, by

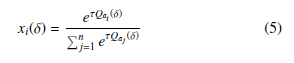
substituting it with biological notions like evolution, mutation, and natural selection [32, 33]. In EGT, there is a genetic encoding of the strategies of the players, which are called genotypes and represent the conduct of every player employed to calculate its outcomes. The quantity of other types of agents in the scenario determines the pay- off of the genotype of each player genotype. In EGT, the population strategies begin to evolve employing a dynamic process that allows

where the notation x_i(δ) means the prospect of using strategy i at time δ, and τ symbolizes the temperature. Equation (5) is well- known as the Boltzmann distribution and is used in [35] to obtain the continuous time model of Q-Learning in the context of a game played by two players, as shown in Equation (6), where ^dxi  is written finding the expected value of this process through the use of the Replicator dynamics equation. An evolutionary system often returns

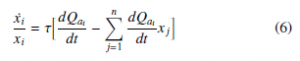
The expression ^dQai (t) in Equation (6) can be solved by using Equation (1) to represent the Q-learner update rule. Equation (7) presents the equation of difference for the function Q.

The term σ expresses the time spent between two repetitions of the Q-values updates, where 0 < σ ≤ 1, while Q_a (δσ) denotes the

3. The Boltzmann-based distributed repli- cator dynamics method

In the following paragraphs, we describe the Boltzmann-based dis- tributed replicator dynamics method. The starting point needed to perform the development of this method is the Equation (11). This formalism is useful since it employs the Boltzmann concept and its σ. Then, by assuming an infinitesimal scheme of first term has the classic form of the RD when modeling games that use payoff matrices. Considering the idea to have an analogous and this expression, Equation (7) converts to Equation (8) after taking the limit σ → 0. more general form to express the RD expression, Equation (11) can be written as Equation (13):

As ^xj  comes to eτ∆Qa j , the part after the sum in Equation (8) can be written in logarithm terms:

In this equation, a fraction of a determined population can aug- ment or diminish depending on the higher/lower fitness values of its individuals with respect to the population average. The population is represented by the state vector x = (x₁, x₂, …, x_n)ⁿ with

The last expression in Equation (8) is reorganized and replaced, so it converts to Equation (10) belong to each of the n-types. In f_i(x), i denotes the fitness type.

Consequently, the fitness average of the population is expressed by f (x) = j x _j f _j(x). Using these assumptions, this expression becomes:

For using payoff matrices in games with two players, Γ_ai as _j a_{i j}y _j can be written, then, the expressions for players 1 and 2 are ex- pressed as shown in Equations (11) and (12), respectively:

The first term of Equation (14) is written as the centralized equa- tion for the RD. We propose to adapt it to a decentralized form, to compute the local information of the players to tackle limitations in communication. The decentralized expression of this step is written

These expressions denote the derivation of the continuous-time model for Q-learning. For the full process of the derivation, see Annex A. The Equations (11) and (12) can be considered as a cen- tralized perspective, analogous to the Equations (3) and (4) that

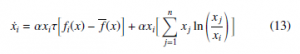
where ⁿ x _j is equivalent to the unit, since the term x _j of the opera- tion denotes the probabilities of selecting the jth strategy. Likewise, when using logarithms rules, the second term in Equation (14) be- comes:

represent the standard RD form to model actions of players R and C, in a game of 2 players. However, the Boltzmann model produces the main differences with the introduction of α and τ parameters,

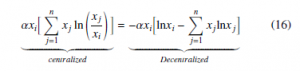
and the emergence of an additional term. This approach has been applied in some scenarios such as multiple state games, multiple player games, and in the context of 2 2 games [27]. Nevertheless, research is still needed to use this approach in real-life problems.

The following Section presents our approach, which is a learn- ing method that uses a distributed population perspective to control agents’ behaviors. This proposal uses some of the principles stated

Finally, substituting Equations (15) and (16) in Equation (14), becomes Equation (17), that expresses the Decentralized form of the Replicator Dynamics equation in connection with Boltzmann probabilities.

in [35] to introduce the Boltzmann-based distributed replicator dynamics approach. This paper also uses the concept of population

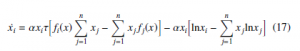
dynamics but employing constraints in the agents communications and assuming players should use neighboring strategies, thus, hav- ing a scenario where players have no full information of the system.

This equation is studied in detail in Section 4 considering EGT with the selection-mutation concept and the exploration-exploitation approaches with their influence on MAS. in Equation (17), the first parenthesis corresponds to alterations in the proportion of players that are using the i-th strategy and require complete information about the state of the whole population and the payoff functions. Consequently, complete information of the system is required so that population dynamics evolve. However, since this work aims to control scenarios where agents cannot access the complete infor- mation of the system, there should not be dependence on complete information, for example, in scenarios with limitations in communi- cation infrastructure, big systems, or privacy matters that obstruct the process of sharing information. Since the population structure determines the features that explain players behaviors, the popu- lation structure in the classic approach owns a complete and well- mixed structure, which means that players can choose any strategy with the same probability as the others. Figure 1a illustrates this concept with some players in a game. We use element shapes such as scissors, paper, or stone to represent the chosen strategies of each agent.

while Figure 2b illustrates the case with constraints in the structure. The form of the graph is determined by the particular structure of the population. In this research, undirected graphs are employed, which means that the probability that strategies j and i find each other are the same as in strategies i and j.

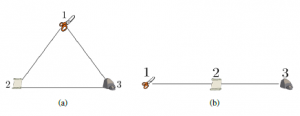
Figure 2: Graphs topology for (a) full and well-mixed structure and (b) constrained structure.

Now, for regulating agents interactions, the limitation of incom- plete information dependency in the population structure of Equa- tion (17) must be overcome. For this purpose, the work proposed by

Figure 1: (a) Population Structure Without Constrains, (b) Constrained Population Structure

Considering EGT, each player can equally obtain a revision opportunity. When receiving this opportunity, players choose ar- bitrarily one of their neighbors and switch their chosen strategy to one of their neighbors based on the selected revision protocol. As players are supposed to have a full and well-mixed structure, any opponent has the same possibility of selecting and playing any strategy of the structure (Figure 1a). On the contrary, Figure 1b

where the calculation of p_i only requires knowing the portions of the population that are playing neighboring strategies. Then, the following expression is assumed:

Assumption 1 Operations that update behaviors of agents by em- ploying the pairwise proportional imitation protocol use the neigh- boring concept, which means that the iterations in the sums and the payoff function are determined by those neighbors communicating effectively with the i-th player.

In this vein, Equation (19) denotes the obtained distributed replicator dynamics that fulfill the limitations of the population structure and enable agents to regulate the calculation of incomplete information:

shows a case where constraints in the structure limit the capacity of an agent to select some strategies, which is also an approach closer revision opportunity, but a neighbor does not have the same proba- bility to choose and play a particular strategy. For instance, when a player obtains a revision opportunity with a paper strategy, there is no opportunity of choosing an opponent with scissors. The reason is that no papers are close to any scissors. Nevertheless, in this player case, the prospect of choosing an adversary with a paper or stone plan is higher than in the scissors situation. The graph G = (T, L, M) establishes a mathematical way to represent the behavior of agents and their dynamics. The set T symbolizes the strategies an agent

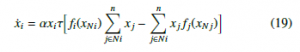
where f_{i/ j}(x_{Ni/ j}) is the payoff function for the ith or jth player, estimated by the proportion of population that effectively communi- cates with neighbors, and ⁿ x _j is a sum that just considers those neighbors who communicate effectively. As our statement about the neighboring concept was implemented just in the first part of Equation (17), the second part of the equation (second parenthesis) including this concept is written as follows:

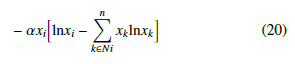
strategy j and i can find each other, but a_{i j} = 0 indicates that these strategies cannot meet. Thence, it is possible to define Ni as the set of neighbors of agent i. Full and well-mixed and constrained mixed populations can be represented by two types of graphs. Figure 2a depicts a complete graph for the full and well-mixed structures, In this equation, k represents i-th neighbor with an active communication link that employs strategy j. The end of the equation expresses the way the i-th player behaves regarding the proposed method using the Boltzmann concept. Equation (21) denotes in a complete manner the Boltzmann-Based Distributed Replicator Dynamics (BBDRD) which includes both concepts: the distributed and the neighboring. to 1, s_ik becomes bigger than or equal to zero. Considering EGT, in the framework of Q-Learning dynamics, mutation is directly con- nected with entropy that expresses the strategy state. However, this connection already existed, since it has been evidenced that entropy

from the perspective of thermodynamics, taking into account the trend of mutation to augment to increase entropy. Additionally, theQ-learning dynamics evidence that RD is the basis for the develop

As stated above, the BBDRD equation evidences the implemen- tation of the exploration and the exploitation notions of RL, and the selection-mutation approach of EGT, as explained in the next section. The implementation of this approach and examples of its application in the context of classic games, maximization problems, and for a smart grid control are developed in Section 5.

4. Evolutionary Approximation

This section presents the control method stated in Equation (21) from the perspective of RL and in an evolutionary approximation, which is helpful to comprehend the introduction of the notion of exploration in the classic RD expression.

4.1        Evolutionary Perspective

The traditional structure of RD is represented in the first part of the dynamics of Equation (21). This allows approximating to the Q-learner dynamics from EGT, because the mechanism for selection is contained in it. Then, the mechanism for mutation is found in the complementary part of the expression, which means:

ment of the selection concept. In RD, the resulting payoff can favor or be independent of a strategy, and the behavior of its opponent is strongly related to the resulting payoff. The concept of mutation can be found too. This fact is estimated by comparing the value of the entropy strategy with the value of entropy of the entire population.

4.2          Reinforcement Learning Perspective

Reinforcement learning aims to compensate the exploration and exploitation mechanisms. For gaining the maximum profit, a player must execute an action. Commonly, the player chooses actions that paid a high compensation before. Nevertheless, if the player wants to identify these actions, it must choose actions that were not chosen before. The notion from RL of exploitation-exploration is under- stood from a biological perspective by establishing connections between exploitation/exploration and mutation/selection. For clarity purposes, the first term of Equation (21) always chooses the best courses of actions, which matches the exploitation concept. Like- wise, the exploration term is introduced into the RD expression due to its direct connection with the terms of entropy in Equation (22). Note that high values of entropy produce a high level of uncertainty

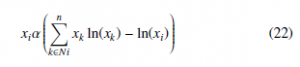
in choosing one course of action. Therefore, the term of exploration augments entropy and gives diversity all at once. Consequently, the exploration and mutation concepts are strongly related, as both

In Equation (22), there are two recognizable entropy values: the distribution of probability x and the value of the strategy x_i. The expressions for entropy can be written as:

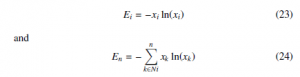
where E_i represents the available information regarding strategy i, while E_n is the information of the complete distribution. Conse- quently, the mutation equation can be expressed now as:

The following expression is the mutation equation derived, con- sidering the difference between old and new states of x_i.

In Equation (26), s_ik expresses the rate of mutation of agents that employ the i-th strategy and select another strategy from the pool of the k neighbors, for example, strategy j. When k is higher or equal

of them give variety, and a feature of heterogeneity to the environ- ment. Being in control of particular scenarios like heterogeneity and communication limitations in a system is a demanding task when addressing real-life cases. In this sense, the compensation of the exploration-exploitation mechanisms can be quite difficult since a fine adjustment is often required for the parameters involved in the learning process. This adjustment must be performed to regulate the behavior of players in the process of decision-making. This problem can be solved by using the BBDRD control method as demonstrated in Equation (21) and explained in the following section.

5. Illustrative cases

5.1          Rock-Paper-Scissors as a classic game

In this part of the document, the concept introduced in Equation

• is implemented in one of the classic games for excellence, the rock-paper-scissors game. For this purpose, a single population with three strategies has been considered, where x = [x₁, x₂, x₃]^t represent each of them respectively. In the same sense, the expres- sion F(x) = Ax denotes the fitness function, where A represents the

payoff matrix showed in Equation (27). It is worth noting that the classic payoff matrix has been modified to guarantee positive values

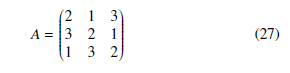
the same simulation parameters were considered, but communi- cation between agents was limited in the following way: agents playing strategy 1 were not allowed to communicate with agents playing strategy 3 and vice versa. Figure 4a shows the behavior of the distributed case, where the graphic seems to be an oval. This To start running the simulation, a time of 30 units was considered with 300 agents and 5000 iterations. Additionally, the following initial conditions were stated x₀ = [0.2, 0.7, 0.1]^t. The classic behavior of the rock-paper-scissors game proposes that every single strategy has the same probability to be selected, which means the absence of a dominant strategy. This behavior can be evidenced using ∆ representation, which is defined as follows:

Definition 1 Let ∆ be the representation of a triangle of n- dimensions known as a Simplex.

Using a simplex helps in the understanding of the implicit dy- namics. Since the simplex is composed of three vertices, each of them represents a strategy e.g. rock, paper, scissors, then, the classic expected simulation of this situation is depicted as shown in Figure (3)a. Similarly, Figure (3)b, shows how the evolution of the popula- tion strategies is completely symmetrical, which means they keep constant along the time.

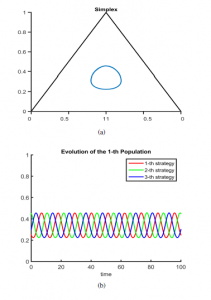
Figure 3: (a) Classic Rock-Paper-Scissors Behavior in a Simplex. (b) Evolution of the Population Behavior.

We also consider simulating a general distributed case to further compare it with the results of the BBDRD method. In both cases, means that the interaction between strategies using only the first part of Equation (21) (general distributed case without entropy) tends to have a similar behavior to the one found in Figure 3a. Additionally, results depicted in Figure 4b show the evolution of the population strategies under the distributed case, where the symmetry is altered by the constraints in the communication of agents.

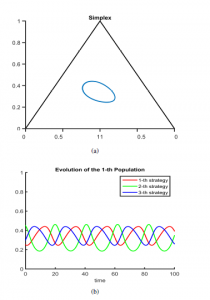
Figure 4: (a) Distributed Rock-Paper-Scissors Behavior in a Simplex. (b) Evolution of the Distributed Behavior.

As mentioned previously, to compare these results with those obtained using the BBDRD method of Equation (21) (Distributed + Entropy case), Figure 5a shows that using τ= 1 the blue line depicts just one part of the oval (in contrast to 4a). Additionally, Figures 5c and 5d show the behavior of the model using τ values of 10 and 100 respectively. As evidenced, the bigger the term τ is, the more similar the behavior is to that obtained in the distributed case i.e. the contour of the oval seems to be equal to that obtained in Figure 4b), which at the same time is similar to the classic case. Finally, In Figure 5b, the evolution of the strategies population seems to be stable in all cases. This can be understood due to the introduction of the entropy term.

5.2        Solving maximization Problems

In this part of the document, we propose an application of the pro- posed method by understanding how it works under single and multi-population cases to solve maximization problems.

• Single Population Case

This case considers a population where each agent can choose one of the n + 1 strategies. In this case, the first n strategy corresponds to one variable of the objective function and the n + 1 th strategy can be seen as a slack variable. Thus, x_k is the proportion of agents that use the kth strategy, and it corresponds to the kth variable, i.e., x_k = z_k. The fitness function of the kth strategy F_k is defined as the derivative of the objective function with respect to the kth variable, thus, Note that if f (x) is a concave function, then its gradient is a de- creasing function. As mentioned previously, users attempt to in- crease their fitness by adopting the most profitable strategy in the population, e.g. the kth strategy. This lead to an increase of x_k, which in turns decrease the fitness F_k(x). Furthermore, the equilib- rium is reached when all agents that belong to the same population have the same fitness. Thus, at equilibrium F_i(x) = F_j(x), where i, j    1, . . . , n . If we define F_n+1(x) = 0, then, at equilibrium F_i(x) = 0 for every strategy i 1, . . . , n . Since the fitness function decreases with the action of users, it can be concluded that the strat- egy of the population evolves to make the gradient of the objective function equal to zero (or as close as possible). This resembles a gradient method to solve optimization problems. Recall that the evolution of the strategies lies in the simplex, that is, _i∈S p z_i = m, thence this implementation solves the following optimization prob-

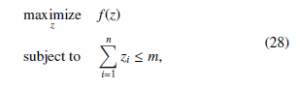
where m is the total mass of the population.

Figure 6 shows an example of the setting described above for the function

Figure 5: (a) Distributed + Entropy Rock-Paper-Scissors Behavior in a Simplex. (b) Evolution of the Population Behavior. (c) Simulation with τ =10. (d) Simulation with τ =100.

Figure 6a shows the classic behavior to solve the maximization problem using a centralized approach. The simulation is executed during 0.6 time units. The black line founds the maximum with a very short deviation. Figure 6b depicts the case using a decentral- ized maximization approach. Once again, the maximum is reached but the deviation is bigger than the centralized approach. Finally, Figures 6c, 6d, 6e and 6f show the behavior of the Boltzmann- Based Distributed Replicator Dynamics, i.e. communication be- tween agents is limited (Equation 21). In these cases, values of τ of 0.1, 0.5, 1, and 10 were used, respectively. Using the ob- tained model, it can be observed that as τ grows, the behavior of the simulation tends to be very similar to that of the centralized approach. Conversely, the shorter the τ value, the farther it is from the maximization point.

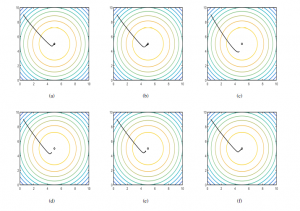
Figure 6: (a) Centralized Maximization Approach. (b) Decentralized Maximization Approach. (c) Distributed Maximization + Entropy Approach for τ =0.1. (d) Distributed Maximization + Entropy Approach for τ =0.5. (e) Distributed Maximization + Entropy Approach for τ =1. (f) Distributed Maximization + Entropy Approach for τ =10

• Multi Population Case

Consider n populations where each agent can choose one out of two strategies. One population is defined per each variable of the maximization problem and also n additional strategies that resemble slack variables. Thus, x^p is the proportion of agents that use the

method evidences that as τ grows, the behavior of the simulation tends to be very similar to that of the centralized approach (where full information is assumed within agents). Conversely, the shorter the ϕ value, the farther and the more deviant it is from the maxi- mization point.

5.3        Smart Grids Application

kth population is defined as the derivative of the objective function with respect to the kth variable, that is, F^k(x) ≡ ∂k f (x). Additionally, F^k(x) = 0. This implementation

solves the following optimization problem:

This part of the paper presents how the use of the Boltzmann-based distributed replicator dynamics can be developed in a power grid. Some of the main issues to solve in these kinds of applications are cases of the economic dispatch problem (EDP). In these problems,

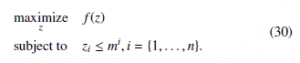
Figure 7a shows the way the system gets to the maximum point using the centralized approach. Using a multi-population, the plot- ted line is made almost without deviations. Similarly, Figure 7b depicts the result for the classical distributed approach, where the multiple populations reach the maximum, but the following form has some deviations before reaching it. Figures 7c, 7d, 7e and 7f show the behavior of the Extended Distributed Replicator Dynamics (see full model of Equation (21)). In these cases, values of τ of 0.1, 0.5, 1, and 10 were used respectively. Results show once again, that using the Boltzmann-Based Distributed Replicator Dynamics power generators, thus fulfilling the limitations of generation capac- ity and power balance simultaneously [38]. In this sense, traditional approaches to EDP have employed offline direct-search methods [21, 15], or static optimization algorithms [20]. One of the first works that introduced a different approach to deal with EDP is [39], where the authors proposed changing the resource allocation as a solution to this issue. Our work takes into account this approach and complements it with the introduction of the Boltzmann-based distributed replicator dynamics as a way to find the place to execute the dispatch algorithm at a microgrid, by using distributed popula- tion dynamics. Our work also assumes that loads, generators, and other devices in the grid share information in the system and have

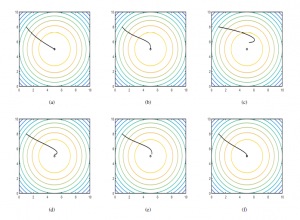
Figure 7: (a) Centralized Maximization Approach. (b) Decentralized Maximization Approach. (c) Distributed Maximization + Entropy Approach for τ =0.1. (d) Distributed Maximization + Entropy Approach for τ =0.5. (e) Distributed Maximization + Entropy Approach for τ =1. (f) Distributed Maximization + Entropy Approach for τ =10

a cooperative role with other controllable devices in the grid. The general case of the microgrid is explained in [40], where authors formulate a grid with two different control levels. At the lowest level, an inverter attaches loads to a source of voltage comprised generation, and J_i(ϕ_i) represents the utility function of every DG. The criterion of the economic dispatch determines the utility func- tion [38], which in turn settles the performance of all the generation units with the same marginal utilities stated in Equation (32) of seven distributed generators (DGs). The output voltage and the operation frequency are controlled by a drop-gain regulator. Figure 8 depicts the distribution of the microgrid.

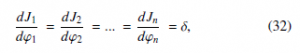
The uppermost level employs a strategy that can dynamically dispatch setpoints of power. The economic limitations, like load demands and power production costs, come from the inferior level of control and are directed to the central controller of the microgrid. Therefore, a classic RD is implemented. The controller obtains dynamic values of load demands and costs, which means that it is possible to include renewable energy resources. As a result, the dispatch is carried out , that is, the uppermost control level. The expression of the EDP is written as follows:

Consider δ > 0, so that ⁿ ϕ_i = ϕ_D. According to the EDP criterion expressed in Equation (32), it is possible that the EDP of Equation (31) obtain a solution by employing utility functions with quadratic form for every DG [39].

5.3.1 The Economic Dispatch Problem Using a Population Games Perspective

From the Population Games Perspective, the EDP can be managed using the Replicator Dynamics approach. For the simulation pur-

poses, we limit the communications constraints among agents at random, which allows us to have another point of view to compare results with those obtained in [1]. Using the population games ap-subject to X ϕ_i  = X ψ_i  = ϕ_D proach, n represents the quantity of DGs in the grid. Consider the

In Equation (31), 0    ϕ_i   ϕ_{max i}, i  Z, n represents the quantity of distributed generators, ϕ_i denotes the the i-th DG set-point of power, ψ_i simbolizes the loads, ϕ_D represents the total load that the power allocated to each DG, which is associated with the number of players that choose the i-th strategy in S. The term ϕ_D represents the sum of every power set-point, which means .n         ϕ_i = ϕ_D to obtain grid requires, ϕ_max establishes the i-th DG maximum capacity of   an appropriate steady-state performance. Likewise, to accomplish

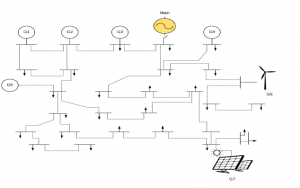
Figure 8: Distribution of a Power Grid. Adapted from [11].

the power balance, f¯   = (1/ϕ_D)     ⁿ     ϕ_i f_i must be implemented to enable the invariance of set ∆ = [ϕ s^t ≥ 0 : _{i s S} ϕi = m] [41]. This equation ensures that in case ϕ(0) s ∆, then ϕ(t) s ∆, ∀t ≥ 0,

by the outcome functions. As a result, the outcome function of each DG can be expressed as:

power by generators. This behavior makes it possible to perform a proper control of frequency. To include in the control strategy economic and technical criteria, the capacity of power generation and the associated cost are relevant factors for determining the final power dispatched to every DG. RD seems to be suitable, since its stationary state is achieved once the average outcome equals all the The population game can transform into a potential game by the addition of marginal utilities to the outcome functions [43]. The out- come functions in Equation (35) become functions of quadratic util- ity for every DG in the optimal EDP [39]. This outcome function has been implemented in other research, e.g. [39, 40, 44].

outcome functions. This characteristic relates RD to EDP, as it is

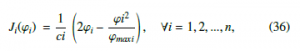
the same as the economic dispatch criterion of Equation (32) when the outcome function is chosen as follows:

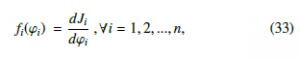
It is worth noting that the EDP approach in Equation (32) ensures an optimal solution of the system if constraints are satisfied. These kinds of optimization issues may be tackled using marginal utilities for the outcome functions. This is possible because the outcome functions are equal to f¯. The outcome chosen can be modeled as an expression whose growth/reduction depends on the distance of the desired set-point from/to the power. In this vein, RD allocate re- sources to generators according to the average result. The following function [42] can illustrate this phenomenon:

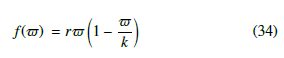
where k represents the carrying capacity so that the independent variable a s (0, K). Here, parameters such as the carrying capacity and a cost factor of generation, among other parameters, are used

5.4        Simulation Results

The BBDRD control model presented in this paper is validated in a study case that considered a low voltage smart grid comprising seven DGs. The system used ϕ_D = 9 kW as the overall power demand in the network; DG 4 had the lowest cost and DG 7 the highest. DGs 1, 3, 5, and 6 had no significant differences in cost, and DG 2 had their lowest cost. The system employs 60 Hz and a nominal capacity of 3.6 kW for all generators, except for DGs 2 and 6 that employ 1.5 KW and 4 KW, respectively. Note that these initial conditions differ from those used in [1], where DG 3 had the lowest cost and the nominal capacity of DGs 2 and DG 6 was 3.6 KW and 2 KW, respectively.

For comparison purposes, first, the classic centralized case was simulated, taking into account the availability of full information. Figure 9a shows the results of this step. There is an unexpected rise in the load of 3 KW and various values for each generator. The frequency was stable, except for t = 0.8, where there is a varia- tion of approximately 0.2 Hz produced by an increase in the load, however, it returns to stability right after it. Figure 9a also depicts the quantity of power delivered to each DG. First, generator DG 7 transmits a minimum power when there is low demand, owing to its costly behavior. On the contrary, DG 3 approximates to its maximum capacity and remains near this value without affectations by changes in the load. In case that the demand augments, DG 7 augments its capacity too, intending to counter-weigh the demand. DG 6 approximated to its maximum capacity just after changes in the load. DGs 1, 4, 5, and 6 evidence a comparable behavior, since they present analogous conditions.   Finally, DG 2 approximates to its maximum performance thanks to its low-cost performance. With the results of the classic centralized case, the BBDRD con- trol method was employed to contrast its behavior. Figure 9b–d present the outcomes of this step for different values of τ. For simulation purposes, we use constraints in the communication of agents at random. When the τ value augments, the system imitates the centralized approach. Low values of τ (Figure 9b) produced the biggest differences, as DGs need more time to achieve their working level. On the contrary, high values of τ (Figure 9d) allow DGs to achieve their working levels faster. Concerning the results obtained in [1], we observe a similar behavior of the microgrid. Despite using limitations in the communications of the generators at random, after employing the BBDRD method with high values of τ, once more the behavior tends to be equal to that of the centralized approach of the classic RD. The main difference evidenced is the behavior of DG4 in comparison with the centralized approach, that is, when the demand augments, it delivers more power as a result of the communication limitations topology and the effect of the exploration concept (second term in Equation (21). This effect was also evidenced in [1] with the behavior of DG5.

6. Conclusions

The Boltzmann-based distributed replicator dynamics shown in Equation (21) might be defined as a learning method of distributed control that includes the exploration scheme from RL in the classic equation of RD. In this sense, exploration can be related to the mutation concept of EGT, and involves a method for measuring variety in the system with the entropy approach. The Boltzmann- based distributed replicator dynamics also employs the scheme of the Boltzmann distribution to include the τ parameter for control- ling purposes. An appropriate temperature function can be chosen using methodological search and reliably set to fulfill an anticipated convergence distribution. Regarding stability, Section 3 presents a derivation process that has low or no significant variations in the presence of multiple agents. This behavior is explained with the inclusion of the population approach in the BBDRD method. The neighboring approach provides the missing piece to prevent cen- tralized schemes from happening and compels players to consider just the available information of other players before performing an action. The method was validated in the context of classic games, maximization problems, and in a smart grid that allowed initializing parameters beforehand, and providing evidence that behavior using the BBDRD approach tends to be similar to cases using centralized schemes.

Engineering problems represent real scenarios whose complex- it can be simulated using MAS, through the analysis of the com- munication between the agents. EGT presents some helpful tools to tackle communication between players and control them. This paper evidences the advantages of applying a distributed control approach of EGT to a real-life smart grid. The BBDRD perfor- mance is presented using experiments that include limitations in communication, therefore, it emerges as a helpful tool for develop- ing more realistic control strategies in Engineering problems with distributed schemes. This advantage becomes particularly relevant because it offers the opportunity to deal with complex systems using local information of the agents, taking into account communication limitations without the need of a centralized coordinator and evad- ing expensive implementation costs, as in classic approaches, like the dual decomposition method. The distributed control concept proposed to tackle cases of classic games, maximization issues, and the Economic Dispatch Problem can be further applied to other real-life situations, including some other problems in the smart grid context, like as the physical limits of power-flow, the presence of power losses, and the inconsistency of renewable generation, among others.

Despite using incomplete information, results demonstrated that the system can imitate the performance of a centralized approach when the τ value increases. conversely, when τ takes values lower than the unit, the behavior was distant from outcomes ob- tained under the optimal communication scenario of a centralized approach. The possibility of adjusting the behavior and parameters of the method using communications limitations between players proved to be successful.   This can also logically be extended to any number of players or populations. Results also evidenced that the Boltzmann-based distributed method has adequate performance for solving some cases of maximization problems, including the economic dispatch problem in a smart grid. This is possible since the features of the DGs were coherent with their power capacity and operation cost.

7. Future Work

For future work, the optimization of wireless sensor networks can be an option for the building automation field. Various critical issues may be tackled by implementing the distributed replicator dynamics approach to solve the EDP in a smart grid scenario, for example, considering power losses, the limitations of physical power-flow, or the uncertainty of renewable generation. Open issues should be considered with respect to the control strategies developed that must include decentralization, scalability, and robustness. In con- sequence, novel methods should incorporate economic incentives and the information necessary to ensure that more elements can be included in the system without a reconfiguration of the whole system. The Boltzmann-based distributed concept that tackles EDP will be expanded to other problems in the context of a smart grid framework, for example, the inconsistency in renewable generation, physical limitations of power-flow, and incorporation of power loss. In summary, distributed techniques used to manage open problems represent a suitable option for modeling the complexity of these sce- narios. Innovative approaches are still required to include scalable solutions and features closer to reality.

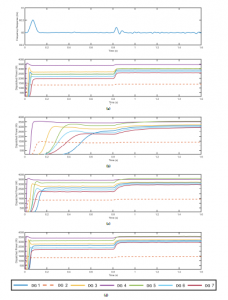
Figure 9: Results for a microgrid system. (a) Frequency response and active power response of DGs for the classic RD. The analysis of the performance of the Boltzmann-based distributed replicator dynamics for different values of τ: (b) τ = 0.4 (c) τ = 2.5, (d) τ = 7.

Conflict of Interest The authors declare no conflict of interest.

Funding This research was funded by Colciencias, grant Doctor- ado Nacional number 727.

1. G. Chica, E. Mojica, E. Cadena, “Boltzmann-Based Distributed Replicator Dynamics: A Smart Grid Application,” in 2020 Congreso Internacional de Innovacio´n y Tendencias en Ingenier´?a (CONIITI), 1–6, IEEE, 2020, doi: https://doi.org/10.1109/CONIITI51147.2020.9240335.
2. J. Barreiro-Gomez, G. Obando, N. Quijano, “Distributed population dy- namics: Optimization and control applications,” IEEE Transactions on Sys- tems, Man, and Cybernetics: Systems, 47(2), 304–314, 2016, doi: 10.1109/TSMC.2016.2523934.
3. G. Chica-Pedraza, E. Mojica-Nava, E. Cadena-Mun˜oz, “Boltzmann Distributed Replicator Dynamics: Population Games in a Microgrid Context,” Games, 12(1), 1–1, 2021, doi:https://doi.org/10.3390/g12010008.
4. G. Bacci, S. Lasaulce, W. Saad, L. Sanguinetti, “Game theory for net- works: A tutorial on game-theoretic tools for emerging signal processing applications,” IEEE Signal Processing Magazine, 33(1), 94–119, 2015, doi: https://doi.org/10.1109/MSP.2015.2451994.
5. C. Mu, K. Wang, “Approximate-optimal control algorithm for constrained zero-sum differential games through event-triggering mechanism,” Non- linear Dynamics, 95(4), 2639–2657, 2019, doi:https://doi.org/10.1007/ s11071-018-4713-0.
6. M. Zhu, E. Frazzoli, “Distributed robust adaptive equilibrium computa- tion for generalized convex games,” Automatica, 63, 82–91, 2016, doi: https://doi.org/10.1016/j.automatica.2015.10.012.
7. S. Najeh, A. Bouallegue, “Distributed vs centralized game theory-based mode selection and power control for D2D communications,” Physical Communica- tion, 38, 100962, 2020, doi:https://doi.org/10.1016/j.phycom.2019.100962.
8. R. Tang, S. Wang, H. Li, “Game theory based interactive demand side man- agement responding to dynamic pricing in price-based demand response of smart grids,” Applied Energy, 250, 118–130, 2019, doi:https://doi.org/10.1016/ j.apenergy.2019.04.177.
9. K. Fra¨mling, “Decision theory meets explainable ai,” in International Work- shop on Explainable, Transparent Autonomous Agents and Multi-Agent Sys- tems, 57–74, Springer, 2020, doi:https://link.springer.com/chapter/10.1007/978-3-030-51924-7 4.
10. A. Navon, G. Ben Yosef, R. Machlev, S. Shapira, N. Roy Chowdhury, J. Belikov  Orda, Y. Levron, “Applications of Game Theory to Design and Operation of Modern Power Systems: A Comprehensive Review,” Energies, 13(15), 3982, 2020, doi:https://doi.org/10.3390/en13153982.
11. N. Quijano, C. Ocampo-Martinez, J. Barreiro-Gomez, G. Obando, A. Pan- toja, E. Mojica-Nava, “The role of population games and evolutionary dy- namics in distributed control systems: The advantages of evolutionary game theory,” IEEE Control Systems Magazine, 37(1), 70–97, 2017, doi: 10.1109/MCS.2016.2621479.
12. M. Lanctot, E. Lockhart, J.-B. Lespiau, V. Zambaldi, S. Upadhyay, J. Pe´rolat, S. Srinivasan, F. Timbers, K. Tuyls, S. Omidshafiei, et al., “OpenSpiel: A frame- work for reinforcement learning in games,” arXiv preprint arXiv:1908.09453, 2019.
13. W. H. Sandholm, Population games and evolutionary dynamics, MIT press, 2010.
14. L. Hindersin, B. Wu, A. Traulsen, J. Garc´?a, “Computation and simulation of evolutionary Game Dynamics in Finite populations,” Scientific reports, 9(1), 1–21, 2019, doi:https://doi.org/10.1038/s41598-019-43102-z.
15. D. P. Palomar, M. Chiang, “A tutorial on decomposition methods for network utility maximization,” IEEE Journal on Selected Areas in Communications, 24(8), 1439–1451, 2006, doi:https://doi.org/10.1109/JSAC.2006.879350.
16. J. R. Marden, “State based potential games,” Automatica, 48(12), 3075–3088, 2012, doi:https://doi.org/10.1016/j.automatica.2012.08.037.
17. L. Zhao, J. Wang, J. Liu, N. Kato, “Optimal edge resource allocation in IoT-based smart cities,” IEEE Network, 33(2), 30–35, 2019, doi:https:
    //doi.org/10.1109/MNET.2019.1800221.
18. A. Cagnano, E. De Tuglie, P. Mancarella, “Microgrids: Overview and guide- lines for practical implementations and operation,” Applied Energy, 258, 114039, 2020, doi:https://doi.org/10.1016/j.apenergy.2019.114039.
19. J. P. Lopes, C. Moreira, A. Madureira, “Defining control strategies for mi- crogrids islanded operation,” IEEE Transactions on power systems, 21(2), 916–924, 2006, doi:https://doi.org/10.1109/TPWRS.2006.873018.
20. T. Ibaraki, N. Katoh, Resource allocation problems: algorithmic approaches, MIT press, 1988.
21. S.-J. Ahn, S.-I. Moon, “Economic scheduling of distributed generators in a microgrid considering various constraints,” in 2009 IEEE Power & Energy Society General Meeting, 1–6, IEEE, 2009, doi:https://doi.org/10.1109/PES. 2009.5275938.
22. G. Strbac, “Demand side management: Benefits and challenges,” Energy policy, 36(12), 4419–4426, 2008, doi:https://doi.org/10.1016/j.enpol.2008.09.030.
23. D. E. Olivares, C. A. Can˜izares, M. Kazerani, “A centralized optimal energy management system for microgrids,” in 2011 IEEE Power and Energy Soci- ety General Meeting, 1–6, IEEE, 2011, doi:https://doi.org/10.1109/PES.2011. 6039527.
24. P. Quintana-Barcia, T. Dragicevic, J. Garcia, J. Ribas, J. M. Guerrero, “A distributed control strategy for islanded single-phase microgrids with hybrid energy storage systems based on power line signaling,” Energies, 12(1), 85, 2019, doi:https://doi.org/10.3390/en12010085.
25. B. Huang, L. Liu, H. Zhang, Y. Li, Q. Sun, “Distributed optimal economic dispatch for microgrids considering communication delays,” IEEE Transac- tions on Systems, Man, and Cybernetics: Systems, 49(8), 1634–1642, 2019, doi: 10.1109/TSMC.2019.2900722.
26. J. C. Vasquez, J. M. Guerrero, J. Miret, M. Castilla, L. G. De Vicuna, “Hierar- chical control of intelligent microgrids,” IEEE Industrial Electronics Magazine, 4(4), 23–29, 2010, doi:https://doi.org/10.1109/MIE.2010.938720.
27. D. Bloembergen, K. Tuyls, D. Hennes, M. Kaisers, “Evolutionary dynamics of multi-agent learning: A survey,” Journal of Artificial Intelligence Research, 53, 659–697, 2015, doi:https://doi.org/10.1613/jair.4818.
28. H. Peters, Game theory: A Multi-leveled approach, Springer, 2015.
29. R. S. Sutton, A. G. Barto, Reinforcement learning: An introduction, MIT press, 2018.
30. W. Ertel, “Reinforcement Learning,” in Introduction to Artificial Intelligence, 289–311, Springer, 2017.
31. F. L. Da Silva, A. H. R. Costa, “A survey on transfer learning for multiagent reinforcement learning systems,” Journal of Artificial Intelligence Research, 64, 645–703, 2019, doi:https://doi.org/10.1613/jair.1.11396.
32. T. Bas¸ar, G. Zaccour, Handbook of Dynamic Game Theory, Springer, 2018.
33. J. Newton, “Evolutionary game theory: A renaissance,” Games, 9(2), 31, 2018, doi:https://doi.org/10.3390/g9020031.
34. J. W. Weibull, Evolutionary game theory, MIT press, 1997.
35. K. Tuyls, K. Verbeeck, T. Lenaerts, “A selection-mutation model for q-learning in multi-agent systems,” in Proceedings of the second international joint con- ference on Autonomous agents and multiagent systems, 693–700, 2003, doi: https://doi.org/10.1145/860575.860687.
36. A. E. Eiben, J. E. Smith, Introduction to Evolutionary Computing, Springer, 2015.
37. D. Stauffer, “Life, love and death: Models of biological reproduction and aging,” Institute for Theoretical physics, Ko¨ln, Euroland, 1999.
38. W. Aj, B. Wollenberg, “Power generation, operation and control,” New York: John Wiley & Sons, 592, 1996.
39. A. Pantoja, N. Quijano, “A population dynamics approach for the dispatch of distributed generators,” IEEE Transactions on Industrial Electronics, 58(10), 4559–4567, 2011, doi: https://doi.org/10.1109/TIE.2011.2107714.
40. E. Mojica-Nava, C. A. Macana, N. Quijano, “Dynamic population games for optimal dispatch on hierarchical microgrid control,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, 44(3), 306–317, 2013, doi: https://doi.org/10.1109/TSMCC.2013.2266117.
41. J. Hofbauer, K. Sigmund, et al., Evolutionary games and population dynamics, Cambridge university press, 1998.
42. N. F. Britton, Essential mathematical biology, Springer Science & Business Media, 2012.
43. H. P. Young, S. Zamir, “Handbook of Game Theory with Economic Applica- tions,” Technical report, Elsevier, 2015.
44. E. Mojica-Nava, C. Barreto, N. Quijano, “Population games methods for distributed control of microgrids,” IEEE Transactions on Smart Grid, 6(6), 2586–2595, 2015, doi:https://doi.org/10.1109/TSG.2015.2444399.

(Click Here)