1. Introduction

Cooperation between multiple robots is one method to complete large-scale and parallel tasks that a single robot cannot solve alone. Swarm robotic systems achieve this cooperative capability without centralized control by implementing swarm intelligence. In this system, a swarm of robots behaves in an organized manner through robot interactions [1]. When robots must complete a complex task that requires object transportation and tracking, they must move in a group or swarm. Various methods have been studied to determine swarm behaviors suitable for the task. Heavy object transportation requires a high-density robot swarm to support the weight. In contrast, the transport of light objects requires a low-density robot swarm to reduce the number of operating robots. In addition, monitoring dynamic targets, such as a school of fish, requires a low-density robot swarm to expand and optimize the observation range. Swarm robotics requires adaptive swarm behaviors that control robots to achieve different densities and shapes.

Swarm behavior control for object transportation robots includes collective movements in which the robot swarm moves while maintaining either a pre-organized shape in a two-dimensional [2] or three-dimensional space [3], or a flock, in which robots move while changing their arrangement to adapt to the velocities and positions of other robots [4, 5]. These approaches typically control the robots using local interactions based on inter-robot relative distances and orientations [6], global interactions based on a virtual leader robot [7], environmental geometry, and the positions of the robots [8]. Local interactions distribute control based on the states of neighboring robots; formations determined in this way must place robots at intervals in which they recognize their neighbors. Robots can build a dense hexagonal close-packed structure to ensure that they do not deform, split, or break formation, while at the same time prioritizing swarming [9] or area cover [10]. Global interactions, on the other hand, require centralized control to share arbitrary information. Formations constructed using this method can freely position the robots individually. The number of controllable robots in this global-control scheme then depends on the communication performance of the robots and the computational performance of the centralized control unit. Hence, distributed control based on local information is advantageous when controlling a large-scale robot swarm. However, the formations constructed under this control method cannot provide density and area coverage suitable for many cooperative tasks with different densities. Therefore, we consider a method for constructing and moving a large-scale robot swarm with different densities, scales, and shapes to perform cooperative tasks. Cooperation between multiple robots is one method to complete large-scale and parallel tasks that a single robot cannot solve alone. Swarm robotic systems achieve this cooperative capability without centralized control by implementing swarm intelligence. In this system, a swarm of robots behaves in an organized manner through robot interactions [1]. When robots must complete a complex task that requires object transportation and tracking, they must move in a group or swarm. Various methods have been studied to determine swarm behaviors suitable for the task. Heavy object transportation requires a high-density robot swarm to support the weight. In contrast, the transport of light objects requires a low-density robot swarm to reduce the number of operating robots. In addition, monitoring dynamic targets, such as a school of fish, requires a low-density robot swarm to expand and optimize the observation range. Swarm robotics requires adaptive swarm behaviors that control robots to achieve different densities and shapes.

Figure 1 shows two types of structures based on connections between neighboring robots: crystalline structures, which arrange robots in a regular tessellation [11], and amorphous structures, which place robots in an irregular pattern suited to a given condition [12]. Comparing the density of each crystalline structure when packed by circular robots, the hexagonal lattice is the highest, and the honeycomb lattice is the lowest, depending on the number of neighbors. In crystalline structures, robots can maintain their construction with only the relative angles and distances between them, making the formations match the constructed lattice. In contrast, an amorphous structure has irregular angles between neighboring robots. Therefore, the swarm shape can meet evolving environmental requirements. Amorphous swarms also prevent splitting by reinforcing high-load sections during transportation. However, owing to these properties, amorphous structures cannot build a shape with high density. This study focuses on crystalline robotic formations to stably control swarms with different densities.

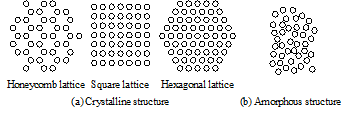
Figure 1: Examples of crystalline and amorphous structures

Regular tessellations provide latticed structures with high density by arranging the robots according to geometric constraints. The study of modular robots in lattice structures has facilitated the development of self-organizing robots with angular joints between neighbors in honeycomb, square, and hexagonal lattices [13, 14, 15]. These robots can self-organize various swarm shapes by recursively communicating with their neighbors, and can behave rigidly as they are physically interconnected with neighboring robots. However, these modular robots cannot organize other lattice formations owing to the physical constraints of their joint assemblies. In this study, we design a virtual interaction to construct lattice-based swarm shapes without the physical restriction of joints, such as the joint limits of modular robots. In our previous study, we proposed a collective movement using a distance-based local interaction based on the Lennard-Jones potential, an intermolecular potential [16]. This potential converges into a hexagonal close-packed structure, as described above. This study develops a group-forming model that adds an angular potential to this distance potential. For collective movement, the method introduces a leader-follower control, in which the robots orient with respect to a single leader robot in the group. Host systems and operators can then control the robot swarm by managing only the path of the leader. Therefore, the system does not require a large-capacity network to connect all robots. The above global-information-based approach can achieve collective movement without this physical leader by introducing a goal location and a virtual leader. For the host system to broadcast such information to the swarm, the system must either deploy an area network to communicate the information to all robots or equip them with a sensor device that can detect the direction of a physical goal, such as a light [17] or sound [18]. The robots then move autonomously toward the position indicated by the global information. Unfortunately, it is difficult for systems to manage the moving path of the whole swarm because the robots move autonomously. Therefore, this study considers the collective movement of a large-scale robot swarm using leader-follower control, controlling the swarm path in real-time by communicating with a single robot. We developed a collective movement method for a robot swarm with a density, scale, and shape suitable for cooperative tasks solved by robot swarms via teleoperation of a leader robot. This paper shows that a robot swarm applying the proposed method can move while maintaining various swarm shapes constructed with different densities.

The rest of this paper is structured as follows: Section 2 describes the configuration of the robot swarm and mathematical variables. Section 3 proposes a group-forming potential and collective movement method using leader-follower control. In Section 4, we discuss changing the robot swarm structures, and apply the changes during movements with different densities, sizes, and shapes. Finally, Section 5 summarizes the study.

2.      Preliminaries

The robot swarm used in this study consists of two or more homogeneous mobile robots that may move within a linearly controllable speed v_max in all directions in a two-dimensional plane without any obstacles. The robot is equipped with both a distance sensor, such as light detection and ranging (LiDAR), to obtain the relative positions of surrounding neighbor robots and a local communication device, such as an infrared communicator, to exchange unique information with neighbors detected by the sensor. The position information is input to the proposed controller. As shown in Figure 2, the controller recognizes the neighbors to construct the lattice connected by the red lines among the communicable neighbors in all directions. The outer shape of the robots is circular with a diameter of σ [m] to prevent the occurrence of distance error due to robots measuring each other from all directions. All robots require a shared common reference direction to determine their neighboring angles and construct lattice structures; to provide this orientation, we initialize the robots with the same heading or synchronize directional information by averaging the data through local communication [19]. The i-th robot obtains the physical information of a neighbor robot with a distance-vector r_ij , composed of the distance ||r_ij|| and the direction angle θ_ij, to the j-th neighboring robot.

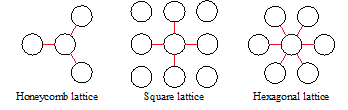
Figure 2: Neighbors that can communicate with the central robot in each latticed structure. The red line represents the connection with the neighboring robots equidistant from the central robot.

3.      Multi-Robot Movement Control Method

3.1.  Group-forming potential with latticed structures

Geometric swarm tessellations depend on the distance and angle between neighboring robots, treated as points. To maintain the structure of these points, distance and angle are used to compute and converge on a target structure. We propose a virtual potential-based interaction that depends on the relative position of neighboring robots to maintain cohesion.

Regarding the distance potential, we took inspiration from the interaction of molecules that organize molecular lattice structures. Among the various potential models that describe molecular bonds, the Lennard-Jones potential [20] is calculated with simple operations. With this potential, the repulsive and attractive forces diverge to infinity as the distance between molecules shrinks with an arbitrary maximum value determined by a coefficient past a certain distance depending on the molecular diameter. Considering the robot as a molecule, this study modifies the potential using the normalized coefficient adjusted to ensure that the maximum attractive force is one; the force on the relative distance, which is the first-order derivative of the Lennard-Jones potential, is expressed as follows:

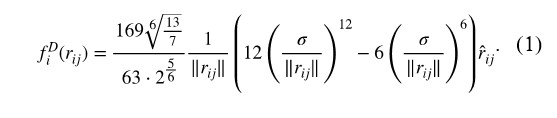
The robot moves according to the calculated force, converging to a distance of ||r₀||, where f_i^D′(r₀) = 0, depending on the diameter. The robots are controlled only by this potential move toward the balance distance between themselves and their neighbors, moving freely about a circle of radius ||r₀||. Consequently, the robots organize into a close-packed hexagonal lattice structure. This study introduces an angular potential that converges in equally spaced directions, suitable for lattices with different densities. Robots constructing the lattice structure must place their neighbors in the angular intervals of 2π/3, π/2, and π/3 [rad], divided by the number of connections in honeycomb, square, and hexagonal lattices, respectively, as shown in Figure 2. This study applies a simple angular potential model to converge robots into these lattices, as follows:

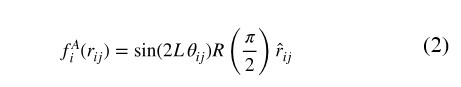
where L is three, four, and six for honeycomb, square, and hexagonal lattices, respectively, matching the number of neighbors constructing the lattice structure. This model works normal to the relative distance vector between each pair of robots and can modify the angular error between robots within ±π/4L [rad]. Thus, the robot moves to arrange its neighbors into angles matching the target lattice structure. By combining the distance and angular potentials, the robots converge into a lattice with their neighbors, as shown in Figure 3. The swarm organized by these robots maintains a latticed structure.

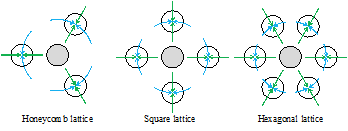
Figure 3: Positions of neighbors converged by the proposed angular and distance potentials

3.2.  Collective movement using potential weights

The collective movement method in this study uses leader-follower control to ensure that the host system can manage the robot swarm similarly to the individual robots. Because the host system controls only the leader, as described above, we consider autonomous decentralized control for followers maintaining positional relationships with their neighbors. The proposed potential models rectify the positional errors caused by an organized latticed structure; if a robot swarm includes a leader, it can move while maintaining formation by adapting to structural changes caused by the leader’s movement. Followers will react to structural changes caused by both the leader and each other, because this interaction affects all neighbors uniformly. Consequently, the approach using the proposed potential models creates a slow and inefficient collective movement for the robots’, limiting formation speed.

We facilitate follower behavior during structural change caused by the leader’s movement by weighting robot interactions. Interactions in the direction of the leader are weighted higher than interactions away from the leader. In a previous study [16], this approach was applied only to the distance potential. This study formulates a collective movement model for followers that introduces additional weights to the model potentials as follows:

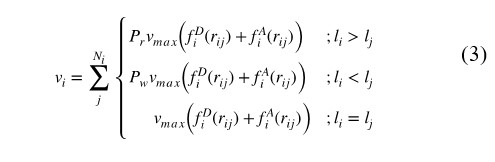
where N_i is the set of neighbors around the i-th robot. The robot applies a weight-adjusted potential to each neighbor, where P_r and P_w are the weights for neighbors closer to or farther from the leader, respectively. These weights are constrained by P_r + P_w = 2 ; (P_r > P_w > 0) to ensure that the adjusted interactions provide the same interaction magnitude as the interactions without the new collective movement approach. Followers weigh their neighbors based on the distance between themselves and the leader. We introduce an ordering layer based on the lattice construction, which represents the routing metric to the leader as shown in Figure 4. The leader is given a layer reference value of zero, and followers set their layer value, l_i, as l_i = min(l_j) + 1 based on the layer value of their neighbors, l_j . The followers update this metric by repeating the calculation by each follower, and quickly produce a radial gradient around the leader. Consequently, each follower adjusts their potential weights according to this gradient to ensure that they more strongly perceive the structural change caused by the leader.

The movement of the leader is teleoperated through a host system to control the destination of the swarm. The leader’s moving vector, related to a given moving command, is as follows:

where P_l is an upper-speed limit coefficient for the leader designed as P_r − 1 to ensure that the leader’s movement does not exceed the convergence force for the neighbors around the leader, as shown in (3). f_c is a velocity vector given via teleoperation that is less than one.

With these control methods, this study realizes the collective movement of a leader-follower robotic swarm while maintaining a lattice swarm shape. The proposed method can be implemented into any swarm shape with lattice construction.

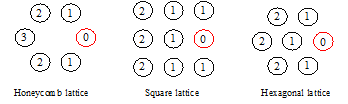
Figure 4: Calculated layer metric between the leader and followers according to the lattice structures

4.      Verification of Collective Movement

Collective movement is an essential technology to support swarm robotic applications. Robot swarms can contribute to cost reduction and efficiency in their applications. In Section 1, we focus on transport and observation tasks using multiple robots, explaining the necessity for unique swarm densities, scales, and shapes. This section confirms that the proposed control method satisfies these goals. The proposed method can control an arbitrary number of robots via distributed control based on local measurements and information exchanged with neighbor robots. This study demonstrates that a robot swarm applying the proposed method can move collectively in all directions, and quantitatively evaluates the scalability of the method for any swarm size [21].

We developed numerical simulations for these evaluations using Java. The robot in this simulation is a moving object with a diameter of 0.25 m, moving with a speed limit of 0.5 m/s. The robot computes a velocity output via the proposed method at 2 ms intervals and simultaneously updates the communicated information. First, this paper evaluate the design and effectiveness (collective movement efficiency) of the parameters for the proposed method, P_r and P_w.

4.1.  Collective movable speed relative to P_r–P_w ratio

The proposed collective movement performance depends on the design of P_r, P_w, and P_l. Therefore, we evaluate the maximum value of the parameter P_l that can be set under the parameters P_r and P_w. Because collective movement must be able to move in all directions, the experiment uses an environment in which formations of each lattice structure with ten-layers filled moves on a circle with a diameter of 10 m.

Figure 5 plots the maximum P_l that did not change in the structure before and after movement, as P_l is increased by 0.01 from zero under each setting P_r and P_w condition. This property also shows the collective movement efficiency for each P_r–P_w ratio. Compared to the condition with P_w = 1, where P_r and P_w were not introduced, the introduction of the P_r–P_w ratio resulted in higher collective movement efficiency. This result also shows that the smaller P_w is, the higher movement efficiency.

We focus on the properties of the proposed method for hexagonal and honeycomb lattices. By introducing an angular potential, the proposed method can detect and adjust the structural changes caused by moving faster than the distance-potential-only collective movement method in the previous study [16]. As a result, the proposed method achieves high collective movement efficiency even for large values of P_w. On the other hand, this property of the square lattice did not improve significantly. This is because the square lattice formation moving in the vertical and horizontal directions has no angular potential action of the neighbors in that direction and less distance potential action for robots closer to the leader. Therefore, the followers could not maintain the connection with the neighbors in the vertical and horizontal movement directions, and the collective movement efficiency decreased.

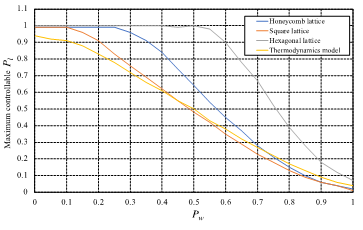
Figure 5: Maximum P_l that can be set according to the P_l–P_w ratio

The proposed collective migration requires the design of parameters, P_r, P_w, and P_l based on Figure 5. In subsequent experiments, P_l, P_r, and P_w are evaluated as 0.5, 1.55, and 0.45, respectively, to ensure that the collective movement efficiency is P_l = 0.5 for all lattices. These parameters are the balance values for the performance of swarm cohesion and collective movement speed, which have a trade-off relationship.

4.2.  Demonstration of collective movement using various swarm shapes

This study focuses on cooperative transportation and sweep coverage using swarm robotics. These tasks require collective movement while maintaining a cohesive robot swarm in the shape of the transported object around its center of gravity [22], or a robot swarm assembled in a row [23].

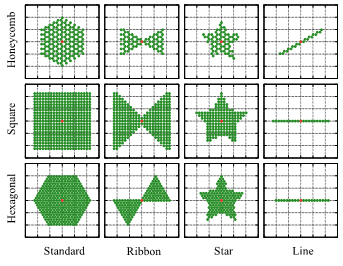
Figure 6: Formations with a scale of ten layers represented according to latticed structures

Therefore, we consider the characteristic formations in a ten-layer formation, as shown in Figure 6. The swarm shapes are as follows: standard formation, which builds a large-scale robot by enlarging the lattice structure around the leader; ribbon formation, which connects two groups at the leader position to transport multiple objects simultaneously; star formation, which is an example of an arbitrary swarm shape represented by a latticed structure, and line formation, which provides an efficient sweep. We confirm that robots implementing the proposed method can move in all directions without breaking formation by demonstrating circular movement.

Figure 7 shows the trajectories of all robots during the movement using these formations. The leader of each formation moves counterclockwise. In all conditions, followers move alongside the remotely controlled leader. This means that while the robots move according to the proposed method, they maintain their positional relationships with each other in a latticed structure. Followers move while modifying the structural changes caused by the movement of robots in the inner layer. Thus, the standard and star formations, arranging the robots to fill the inner layer, transmit their changes to the outer followers from both directions. In contrast, the line and ribbon formations cannot react as strongly, because formations with reduced interconnectivity cannot transmit the information required for the proposed method fast enough to achieve perfect collective movement; this suggests that the proposed method works best when the followers and the leader are adjacent.

Figure 7: Movement trajectories of robots during collective movement in a circle using the formations shown in Figure 6. Each leader moves along the red arrow.

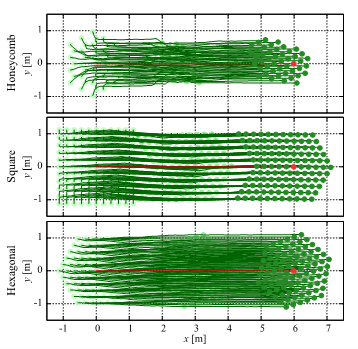
Figure 8: Movement trajectories of robots during collective movement in a straight line using standard formations for each lattice without the proposed angular potential

Subsequently, we confirm the structure-maintaining effect of the proposed method by comparing it with an existing collective movement method that can also maintain a high-density state. As already demonstrated, the proposed method organizes lattice structures using direction and distance potentials. In contrast, many existing collective movement methods control robots using interaction models without angular potentials. As a comparison, we employ a similar swarm behavior model for maintaining a high-density shape in an open space without obstacles that also applies the same Lennard-Jones potential and leader-follower control scheme as shown in our previous study [16]. We apply this existing method to a robot swarm initially arranged in a latticed structure and track their movement trajectories during collective movement. The robot swarm consists of a standard formation with five layers and moves in a straight 3 m line.

Figure 8 shows the movement trajectories of the robot swarm in standard formations with each lattice. The robot swarms arranged in honeycomb and square lattices devolved into a hexagonal lattice, while the robot swarm already arranged in a hexagonal lattice did not deform, as it was already in the highest-density state. These results mean that the angular potential applied in this paper maintains these regular latticed structures.

4.3.  Evaluation of the scalability of the demonstrated formations

We demonstrated collective movement using robot swarms with a ten-layer swarm. We subsequently verify that the proposed method can provide scalable control by quantitatively evaluating the structural changes of the lattice structure during movement. To quantify structural change in the new potential, we combine the angle and distance errors between inter-neighbor positions during movement as follows:

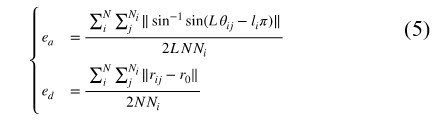
where e_a is the angular error from the l_iπ direction, and e_d is the distance error from r₀, where f ^D(r₀) = 0. These two metrics average values over all N robots in the swarm.

Figure 9 shows the average errors and their deviations during collective movement, with formation size varying in the demonstration from one to seventy layers. The overall result did not show any error divergence caused by lattice structure collapse, because these errors are both much smaller than the angles π/12, π/16, and π/24 [rad] that can be created by the angular potential for honeycomb, square, and hexagonal lattices, respectively, and the distance r_m [m], the radius with the greatest distance potential attraction where f_i^D′′ (r_m + r₀) = 0. Where the number of robots is small, these values do not give accurate averages and are noisy. Thus, these series showed notably small values at small scales.

In line formations, robots have neighbors in chains for angular and distance comparisons regardless of the lattice type. That is, hexagonal, honeycomb, and hexagonal lattices all form a line. First, the distance errors changed with a similar magnitude regardless of the lattice structure used, because the proposed method applies the same distance potential to all latticed structures. In contrast, the angular errors were the largest for the honeycomb lattice and the smallest for the hexagonal lattice. This result means that the angular potential has a different performance depending on the lattice, as noted in the demonstration. The proposed angular potential has a convergence period based on the number of neighbors, L, to ensure that angular convergence occurs according to the angular properties of the lattice structures. Using this design, the convergence range of the angular potential is inversely proportional to L. Therefore, the angular potential of the honeycomb lattice has a wide convergence range while the hexagonal lattice has a narrow convergence range. To achieve the same shape-maintaining performance on all lattices, we should improve the angular potential to ensure that it works regardless of the lattice structure in question.

4.4.  Limitations of the proposed method

In Figure 7 and 9, the entire robot swarm held formation. However, the swarm propagates local angular and distance errors to followers in subsequent layers. Therefore, the formation of the robot swarm should arrange the robots radially to ensure that the structural changes caused by the leader movement propagate quickly along the shortest possible route. The robot swarms used in this study, designed for practical applications, satisfy this requirement. To test the importance of radial error propagation, we consider collective movement under spiral formations that do not arrange robots radially. The followers in this formation were physically placed near the robots closer to the center. However, they only detect structural changes through neighbors in the spiral chain and ignore radial neighbors. Therefore, followers will have difficulty maintaining their shape owing to long delays when detecting structural changes in the formation. This study simulates the movement using spiral formations constructed with each lattice structure, as shown in Figure 10.

The robots arranged in a spiral pattern moved from left to right. Followers close to the leader maintained their structure, while followers on the outer periphery at higher layers experienced structure collapse. As expected, the proposed method could not maintain spiral formations in latticed structures. This limitation is unimportant for transportation and sweeping applications, because these applications rely on close packed lattice formations, rather than long-delay spiral formations. However, we will improve the proposed method to ensure robot swarms can be controlled with long delays in detecting structural changes, such as spiral formations for other applications.

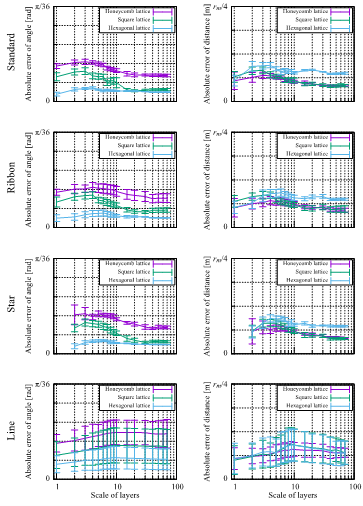
Figure 9: Angle and distance deflections during collective movements in various formations and lattices

5.      Conclusion

Robotic cooperation and coordination is essential for a swarm robotic system when transporting long, large, heavy objects and observing over a wide area. Robots can efficiently complete these tasks by using a swarm with a suitable density for the task. Therefore, this paper proposed a structure-maintaining potential that can control swarm formations in regular tessellations and a collective movement method for a robot swarm using leader-follower control with a host system whereby an operator can handle the entire swarm as a single, large, and mobile robot. This study confirmed that the proposed method could maintain a structure with different densities during collective movement with four formations. The swarm control was evaluated and verified under various formation sizes regardless of formation lattice and scale, reacting to the movement of the swarm leader. The host system can lead a scalable robot swarm from a single robot using the proposed method of leader-follower control. Therefore, the system can distribute control to multiple robot swarm systems in various use cases, such as parallel transportation and environmental exploration. This approach allows robotic swarm systems to obtain higher resolution and larger scales. This approach can contribute to the flexible operation of robot swarms while reducing economic cost.

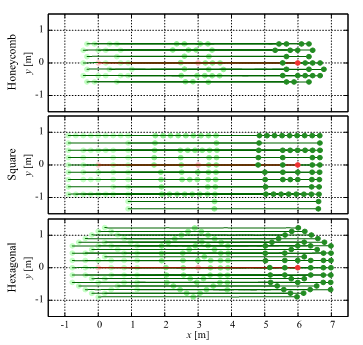
Figure 10: Movement trajectories of robots during collective movement in a straight line using spiral formations with long delays in the propagation of the movement information

In future work, we will develop autonomous collision avoidance and navigation for multiple robot swarms with different scales instead of multiple mobile robots in parallel distributed systems. We improve the proposed method to control even slow propagating formations of structural changes. In addition, the proposed method targets omnidirectional agents such as Omni-wheeled vehicles and multi-copters. Therefore, it does not consider nonlinear dynamics such as nonholonomic constraints. To implement this method on robots with various dynamics, we will develop a method that dynamically shares the direction of movement.

Acknowledgment

This work was supported by the Research Institute for Science and Technology of Tokyo Denki University (grant number Q21DS-03 / Japan). We would like to thank Editage (www.editage.com) for English language editing.

1. M. Schranz, M. Umlauft, M. Sende, W. Elmenreich, “Swarm Robotic Behaviors and Current Applications,” Frontiers in Robotics and AI, 7, 2020, doi:10.3389/frobt.2020.00036.
2. J. Wiech, V. A. Eremeyev, I. Giorgio, “Virtual spring damper method for nonholonomic robotic swarm self-organization and leader following,” Continuum Mechanics and Thermodynamics, 30(5), 1091–1102, 2018, doi: 10.1007/s00161-018-0664-4.
3. Y. Kambayashi, H. Yajima, T. Shyoji, R. Oikawa, M. Takimoto, “Formation Control of Swarm Robots Using Mobile Agents,” Vietnam Journal of Computer Science, 6(2), 193–222, 2019, doi:10.1142/S2196888819500131.
4. F. Dai, M. Chen, X. Wei, H. Wang, “Swarm Intelligence-Inspired Autonomous Flocking Control in UAV Networks,” IEEE Access, 7, 61786–61796, 2019, doi:10.1109/ACCESS.2019.2916004.
5. J. Cheng, B. Wang, “Flocking Control of Mobile Robots with Obstacle Avoidance Based on Simulated Annealing Algorithm,” Mathematical Problems in Engineering, 2020, 2020, doi:10.1155/2020/7357464.
6. A. Casteigts, J. Albert, S. Chaumette, A. Nayak, I. Stojmenovic, “Biconnecting a network of mobile robots using virtual angular forces,” Computer Communications, 35(9), 1038–1046, 2012, doi:10.1016/j.comcom.2011.09.008.
7. T. Yan, X. Xu, Z. Li, E. Li, “Flocking of Multi-agent Systems with Un- known Nonlinear Dynamics and Heterogeneous Virtual Leader,” International Journal of Control, Automation and Systems, 19(9), 2931–2939, 2021, doi:10.1007/s12555-020-0578-3.
8. A.D. Dang, H.M. La, T. Nguyen, J. Horn, “Formation control for autonomous robots with collision and obstacle avoidance using a rotational and repulsive force–based approach,” International Journal of Advanced Robotic Systems, 16(3), 2019, doi:10.1177/1729881419847897.
9. A.M. Parrany, A. Alasty, “Introducing shell formation and a thermodynamics- inspired concept for swarm robotic systems,” Robotics and Autonomous Systems, 148, 2022, doi:10.1016/j.robot.2021.103939.
10. Q. Wang, H. Zhang, “A Self-Organizing Area Coverage Method for Swarm Robots Based on Gradient and Grouping,” Symmetry, 13(4), 2021, doi:10.3390/sym13040680.
11. A. Ekblaw, J. Paradiso, “Self-Assembling Space Habitats: TESSERAE design and mission architecture,” in 2019 IEEE Aerospace Conference, 1–11, 2019, doi:10.1109/AERO.2019.8742122.
12. P. Swissler, M. Rubenstein, “FireAnt3D: a 3D self-climbing robot towards non-latticed robotic self-assembly,” in 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 3340–3347, 2020, doi:10.1109/IROS45743.2020.9341116.
13. Z. Yang, Z. Fu, G. Yu, J. Fei, H. Zheng, “A self-repairing approach for the M-Lattice modular robotic system using digital hormone model,” Robotics and Autonomous Systems, 97, 1–15, 2017, doi:10.1016/j.robot.2017. 08.001.
14. J. W. Romanishin, K. Gilpin, D. Rus, “M-blocks: Momentum-driven, magnetic modular robots,” in 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, 4288–4295, 2013, doi:10.1109/IROS.2013.6696971.
15. A. V. Le, R. Parween, R. Elara Mohan, N. H. K. Nhan, R. Enjikalayil Abdulka- der, “Optimization Complete Area Coverage by Reconfigurable hTrihex Tiling Robot,” Sensors, 20(11), 2020, doi:10.3390/s20113170.
16. K. Yamagishi, T. Suzuki, “Collective Movement Method for Swarm Robot based on a Thermodynamic Model,” International Journal of Advanced Computer Science and Applications, 8(11), 2017, doi:10.14569/IJACSA.2017. 081163.
17. P. Bannur, P. Gujarathi, K. Jain, A. J. Kulkarni, “Application of Swarm Robotic System in a Dynamic Environment using Cohort Intelligence,” Soft Computing Letters, 2, 2020, doi:10.1016/j.socl.2020.100006.
18. T. Kida, Y. Sueoka, H. Shigeyoshi, Y. Tsunoda, Y. Sugimoto, K. Osuka, “Verification of Acoustic-Wave-Oriented Simple State Estimation and Application to Swarm Navigation,” Journal of Robotics and Mechatronics, 33(1), 119–128, 2021, doi:10.20965/jrm.2021.p0119.
19. A. Gutierrez, A. Campo, M. Dorigo, J. Donate, F. Monasterio-Huelin, L. Mag- dalena, “Open E-puck Range Bearing miniaturized board for local communication in swarm robotics,” in 2009 IEEE International Conference on Robotics and Automation, 3111–3116, 2009, doi:10.1109/ROBOT.2009.5152456.
20. N. Yu, A. A. Polycarpou, “Adhesive contact based on the Lennard–Jones po- tential: a correction to the value of the equilibrium distance as used in the potential,” Journal of Colloid and Interface Science, 278(2), 428–435, 2004, doi:10.1016/j.jcis.2004.06.029.
21. M. K. Heinrich, M. D. Soorati, T. K. Kaiser, M. Wahby, H. Hamann, “Swarm robotics: Robustness, scalability, and self-X features in industrial applications,” it – Information Technology, 61(4), 159–167, 2019, doi:10.1515/itit-2019-0003.
22. K. Huang, J. Chen, J. Oyekan, “Decentralised aerial swarm for adaptive and energy efficient transport of unknown loads,” Swarm and Evolutionary Computation, 67, 2021, doi:10.1016/j.swevo.2021.100957.
23. A. S. Matveev, P. A. Konovalov, “Distributed reactive motion control for dense cooperative sweep coverage of corridor environments by swarms of non-holonomic robots,” International Journal of Control, 1–14, 2021, doi:10.1080/00207179.2021.2005258.

(Click Here)